【Python算法】递归与递归式

　　

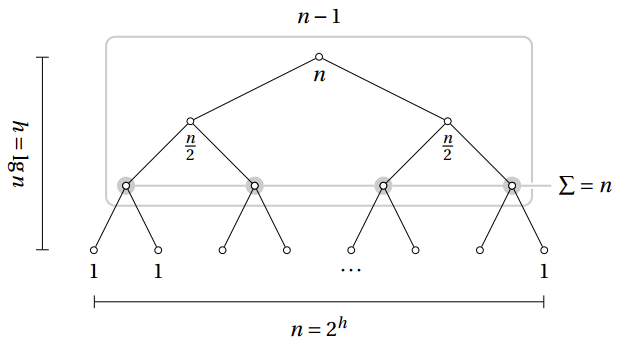
　　该树结构显示了从1(根节点)到n(n个叶节点)的整个倍增过程。节点下的标签表示从n减半到1的过程。

　　当我们处理递归的时候，这些级数代表了问题实例的数量以及对一系列递归调用来说处理的相关工作量。

　　当我们需要找出全部的工作量时，我们需要用到树的高度以及每一层所处理的工作量。每一层总共的标志总数保持在n。

Recursion and Recurrences

def S(seq,i=0):
    if i==len(seq):return 0
    return S(seq,i+1)+seq[i]

　　该求和式从参数i开始，当其值超出目标序列时，函数返回0；否则将i的位置加i，继续求剩下序列的和。

　　计算 S(seq，i) 所需要的时间T(n)等于递归调用 S(seq，i+1) 所需要的时间加上访问 seq[i] 所需的时间。(默认T(k) = Θ(1) , k为常数)

　　可以定义为 T(n) = T(n-1) + 1

　　目标是把递归展开的层数用一个变量i来描述的表达式。

　　将原式中的n值替换为n-1可得 : T(n-1) = T(n-2) + 1

　　

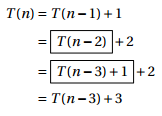
　　假设T(n)递归展开式次数为i，可得：

　　T(n) = T(n-i) + i

　　然后将T(n-i) 变成 T(i)

　　

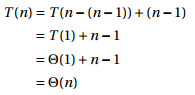
　　所以，函数S是一个线性级的运行时间的操作。

这种方法称为重复带入法，或者迭代法。一般分为以下步骤：

1. 逐步展开递归式，一直到我们发现其中的模式为止。

2. 将该模式表示出来（通常会涉及一个求和式）并用变量i来表示其行号。

3. 根据i层递归将会达到基本情况来选择i的值（并解决该求和式）。

 A Few Important Examples

　　递归式的一般形式：  T(n) = a · T(g(n)) + f(n)，a指递归调用的数量，g(n)递归过程所要解决的子问题大小，f(n)代表了函数中的额外操作。

　 

递归式5：

　　T(n) =  T(n/2) + 1
               = { T(n/4) + 1 } + 1
               = { T(n/8) + 1 } + 1 + 1

　　

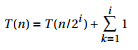
　　令i=lgn ，得到 T(n) = Θ(lgn)

递归式6：

　　

　　

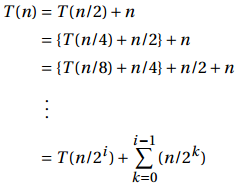
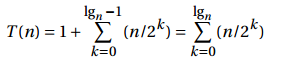
　　if k is a height, then n/2k is the number of nodes at that height . T(n) = Θ(n)

递归式8：

　　

　　

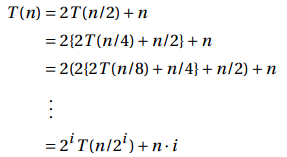
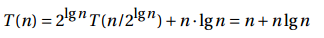
　　递归树根节点上操作时间为n，后面的两次递归调用中，各自执行的都是减半操作，各节点的操作时间等于标签值。

　　每一行的和为n，并且有lgn+1行节点，得出总和为nlgn+n，Θ(nlgn)。

The Master Theorem  主定理

　　递归式与分治法存在的一般关系式为：　　T(n) = aT(n/b) + f(n)

　　主要思想为：有a重调用，每重调用处理掉一定比例的数据（数据集的1/b），还存在一个额外的f(n)操作。

　　

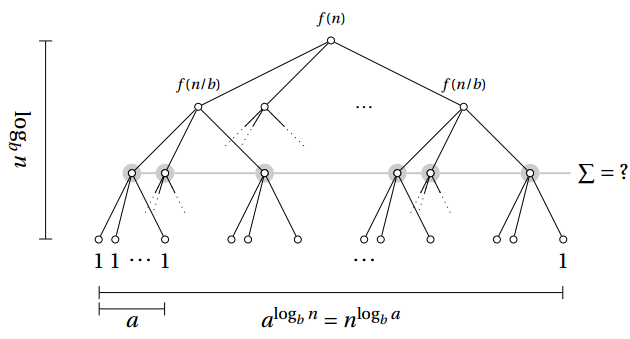
三种基本情况：

1. 大部分操作都是运行在根节点上

2. 大部分操作运行在叶节点上

3. 均匀分布在该递归树的各行之间

①、大部分操作都是运行在根节点上，总运行时间为Θ(f(n))

　　意味着：f(n)增长趋势将严格快于叶节点数的增长。

　　T(n) = Θ(f(n)) = Θ(n)，如果看到b大于a，就立即可以确定n属于表达式的主导部分

②、大部分操作运行在叶节点上

　　

　　例如：T(n) = 2T(n/2)+ lgn ，叶子节点数为n，f(n)=lgn，运行时间就是计算叶节点数的时间 Θ(n)。

③、均匀分布在该递归树的各行之间

　　求该树各层操作之和的求和式

　　

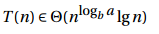
Merge Sort,  归并排序例子：

　　

The input (seq) has a size of n. There are two recursive calls, each on a subproblem of n/2

In addition, there is some work performed in a while loop and in res.reverse();  this work is Θ(n).

This gives us the well-known recurrence number 8, T(n) = 2T(n/2) + Θ(n), which means that the running time of merge sort is Θ(n lg n),  

Summer

The sum of the n first integers is quadratic, and the sum of the lg n first powers of two is linear.

The first of these identities can be illustrated as a round-robin tournament, with all possible pairings of n elements; 

the second is related to a knockout tournament, with lg n rounds, where all but the winner must be knocked out.  

A function is recursive if it calls itself (directly or via other functions). 

A recurrence relation is an equation that relates a function to itself, in a recursive way (such as T(n) = T(n/2) + 1).

These equations are often used to describe the running times of recursive algorithms, and to be able to solve them, we need to assume something about the base case of the recursion;