设计模式之Composite

设计模式总共有23种模式这仅仅是为了一个目的：解耦+解耦+解耦...（高内聚低耦合满足开闭原则）

Composite定义？

将对象以树形结构组织起来,以达成“部分－整体” 的层次结构。

想到Composite就应该想到树形结构图。组合体内这些对象都有共同接口,当组合体一个对象的方法被调用执行时，Composite将遍历(Iterator)整个树形结构,寻找同样包含这个方法的对象并实现调用执行。可以用牵一动百来形容。

Composite好处？

1.使客户端调用简单，客户端可以一致的使用组合结构或其中单个对象，用户就不必关系自己处理的是单个对象还是整个组合结构，这就简化了客户端代码。
2.更容易在组合体内加入对象部件. 客户端不必因为加入了新的对象部件而更改代码。

Composite应用？

1.文件目录与实际目录的展示

Composite模式结构？

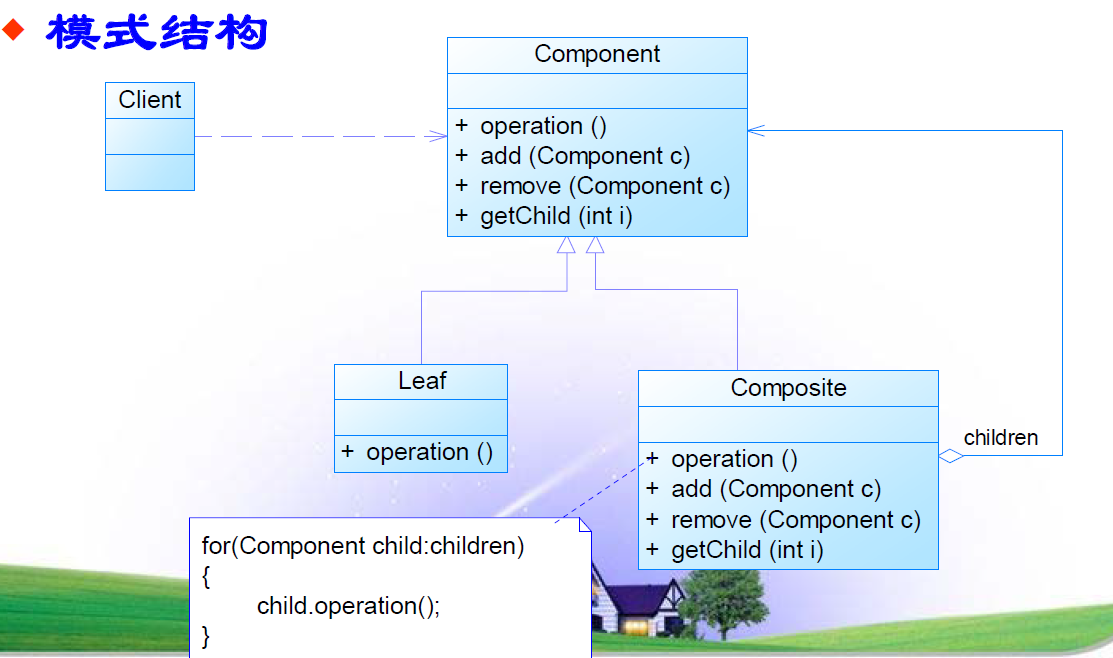
附上Composite的代码：

public class Composite extends Component{

    private ArrayList list = new ArrayList();
    public void add(Component component){ list.add(componet); }
    public void remove(Componet componet){list.remove(component);}
    public Component getChild(int index){ (Component)list.get(index);}
    public void operation(){
        for(Object o : list){
                ((Component)o).operation();
    }

}

这个部分比较好理解。可以与文件系统来举例说明。

一个文件dir里可以有dir也可以有file。dir种可以add/remove dir/file但是file中不能add dir/file。你可以分析出dir中会有一个存放dir/file的list。