lintcode 443.岛屿的个数
在v2ex上看到有人提到了这个,感觉挺简单的,没忍住还是试一下....
基本的染色法。
AC代码:
public class Solution {
/**
* @param grid a boolean 2D matrix
* @return an integer
*/
public int numIslands(boolean[][] grid) {
int res=0;
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[i].length;j++){
if(grid[i][j]){
res++;
solve(grid,i,j);
}
}
}
return res;
}
private void solve(boolean[][] grid,int x,int y){
if(x<0 || x>=grid.length || y<0 || y>=grid[x].length) return ;
if(!grid[x][y]) return ;
grid[x][y]=false;
solve(grid,x+1,y);
solve(grid,x-1,y);
solve(grid,x,y+1);
solve(grid,x,y-1);
}
}
题目来源: http://www.lintcode.com/zh-cn/problem/number-of-islands/
lintcode 443.岛屿的个数的更多相关文章
- LintCode 433. 岛屿的个数(Number of Islands)
LintCode 433. 岛屿的个数(Number of Islands) 代码: class Solution: """ @param grid: a boolean ...
- lintcode:Number of Islands 岛屿的个数
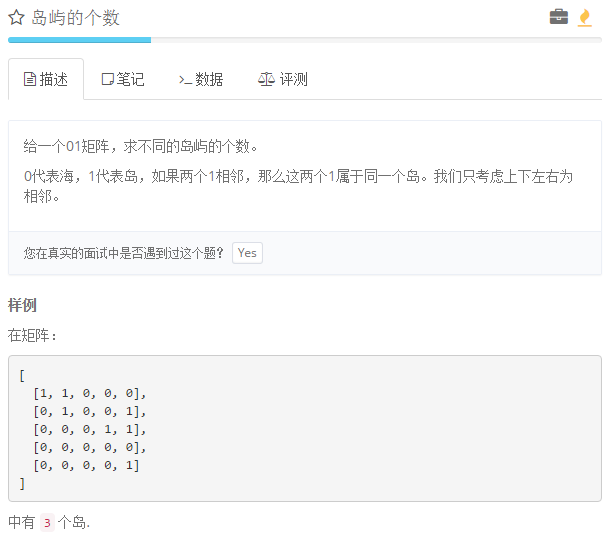
题目: 岛屿的个数 给一个01矩阵,求不同的岛屿的个数. 0代表海,1代表岛,如果两个1相邻,那么这两个1属于同一个岛.我们只考虑上下左右为相邻. 样例 在矩阵: [ [1, 1, 0, 0, 0], ...
- [LeetCode] Number of Distinct Islands II 不同岛屿的个数之二
Given a non-empty 2D array grid of 0's and 1's, an island is a group of 1's (representing land) conn ...
- [LeetCode] Number of Distinct Islands 不同岛屿的个数
Given a non-empty 2D array grid of 0's and 1's, an island is a group of 1's (representing land) conn ...
- leetcode 岛屿的个数 python
岛屿的个数 给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量.一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的.你可以假设网格的四个边均被水包 ...
- 岛屿的个数12 · Number of Islands12
[抄题]: 给一个01矩阵,求不同的岛屿的个数. 0代表海,1代表岛,如果两个1相邻,那么这两个1属于同一个岛.我们只考虑上下左右为相邻. [ [1, 1, 0, 0, 0], [0, 1, 0, 0 ...
- lintcode433 岛屿的个数
岛屿的个数 给一个01矩阵,求不同的岛屿的个数. 0代表海,1代表岛,如果两个1相邻,那么这两个1属于同一个岛.我们只考虑上下左右为相邻. 您在真实的面试中是否遇到过这个题? Yes 样例 在矩阵: ...
- [LeetCode] 711. Number of Distinct Islands II 不同岛屿的个数之二
Given a non-empty 2D array grid of 0's and 1's, an island is a group of 1's (representing land) conn ...
- [LeetCode] 694. Number of Distinct Islands 不同岛屿的个数
Given a non-empty 2D array grid of 0's and 1's, an island is a group of 1's (representing land) conn ...
随机推荐
- Destoon 模板存放规则 及 语法参考
模板存放规则及语法参考 一.模板存放及调用规则 模板存放于系统 template 目录,template 目录下的一个目录例如 template/default/ 即为一套模板 模板文件以 .htm ...
- Linux架设DDNS服务器之自动更新脚本
问题描述:客户端是动态IP,每次连网之后要nsupdate下才可以把客户端的hostname 与IP映射更新到DNS Server上 命令如下: nsupdate -k K*****.key > ...
- jenkins 配置git 学习
由于Jenkins没有默认安装Git插件,需要Git库同步时候,需要手动选择安装git插件 在“系统管理”->“管理插件”中找到,“可选插件”选项卡.“过滤“(一个名为过滤的搜素窗口)中可以用键 ...
- BZOJ4950 Wf2017Mission Improbable(二分图匹配)
先给每个非零格子-1以满足俯视图不变.于是就相当于要求每行每列最大值不变.能减少剩余箱子的唯一方法是在要求相同的行列的交叉处放箱子以同时满足两个需求.给这些行列连边跑二分图匹配即可.注意必须格子初始时 ...
- hdu5279 YJC plays Minecraft 【分治NTT】
题目链接 hdu5279 题解 给出若干个完全图,然后完全图之间首尾相连并成环,要求删边使得两点之间路径数不超过\(1\),求方案数 容易想到各个完全图是独立的,每个完全图要删成一个森林,其实就是询问 ...
- Codeforces 894.C Marco and GCD Sequence
C. Marco and GCD Sequence time limit per test 1 second memory limit per test 256 megabytes input sta ...
- centos7 配置 yum 安装的 jdk
yum 安装的 java,jdk 路径默认是 /usr/lib/jvm/java-* 我们修改 .bash_profile 文件加上下面几行: export JAVA_HOME=/usr/lib/jv ...
- Python2和Python3共存安装
记录下: 先下载Python2.7.6,安装完成,不要添加到path中: 再下载Python3.4.3,安装,不要添加到path中. 进入 Python2: py -2 进入Python3: py - ...
- STL源码分析-内存分配器
http://note.youdao.com/noteshare?id=744696e5f6daf0f2f03f10e381485e67
- 手脱FSG v1.33
1.载入PEID FSG v1.33 (Eng) -> dulek/xt 2.载入OD,先F8跟一会 004103E3 > BE A4014000 mov esi,fsg1_33.0040 ...
