Tarjan 算法详解

一个神奇的算法，求最大连通分量用O（n）的时间复杂度，真实令人不可思议。

废话少说，先上题目

题目描述：

给出一个有向图G，求G连通分量的个数和最大连通分量。

输入：

n,m，表示G有n个点，m条边

下面m行每行包含 x，y，表示有一条x到y的有向边

输出：

第一个数表示连通分量的个数，第二个数代表最大连通分量

输入示例（如下图）

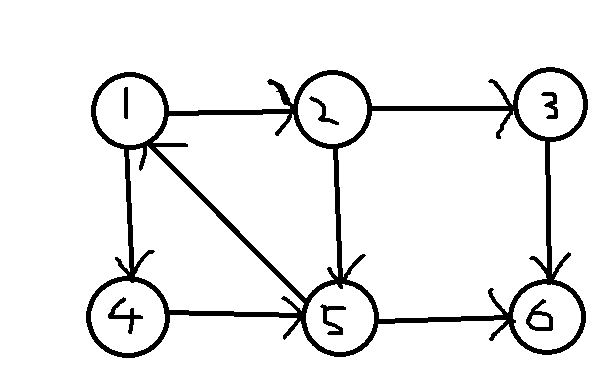
输入示例

很多人会想到DFS，但是时间复杂度为O（n^2），但是时间容易超限，所以我们要用到Tarjan

先理清一下概念：

连通分量：对于图G来的一个子图中，任意两个点都可以彼此到达，这个子图就被称为图G的连通分量（一个点就是最小的连通分量）

最大连通分量：对于图G的一个子图，这个子图为图G的连通分量，且是图G所有连通分量中包含节点数最多的那个，即为G的最大联通分量

时间戳：搜索时第几个搜索到这个点。如搜索顺序是1->2->3->6则6的时间截为4

下面就是tarjan的思路（第一次看不懂可以跳过，直接看详细步骤，回来再看）：

每个点都有两个参数：low，dfn。dfn表示这个点的时间戳，而low代表这个点所能到达的最小的时间戳，开始low都等于dfn，但会经过不断更新而减少。

从1节点进行深度优先搜索，途中用树（一个转化为栈的树）维护。

当遇到一个点时，有如下判断：

1、如果这个点没有访问过，就将这个点加入树（栈）

2、如果这个点访问过，且在树（栈）里，与这个点的low比较，更新自己的low

返回时更新low

当一个点遍历所有的边后这个点的low还是等于dfn，将个点及以上出栈，这个点及栈以上的点构成一个连通分量。

来一点Chinese++（就是伪代码）　　

void tarjan(int 当前点)
{
    这个点的low=dfn=时间戳;
    将这个点入栈;
    标记这个点入栈;
    枚举这个点连接的所有边
    {
        如果目标点没有被访问过
        {
            tarjan(目标点);
            更新当前点的low;
        }
        如果目标点被访问过
        {
            更新当前点的low;
        }
    }
    如果当前点的low==dfn
    {
        将这个点及栈以上的点出栈，标记成一个强连通分量;
        ans++;
    }
} 

详细过程：

开启黑暗之门

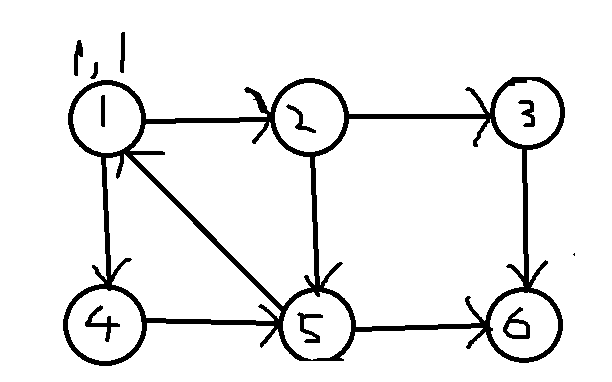
开始，从1节点开始，时间截和low都是1，将1入栈

stack：1,

走到2节点，2的时间戳dfn和low都是2,2入栈

stack：1,2

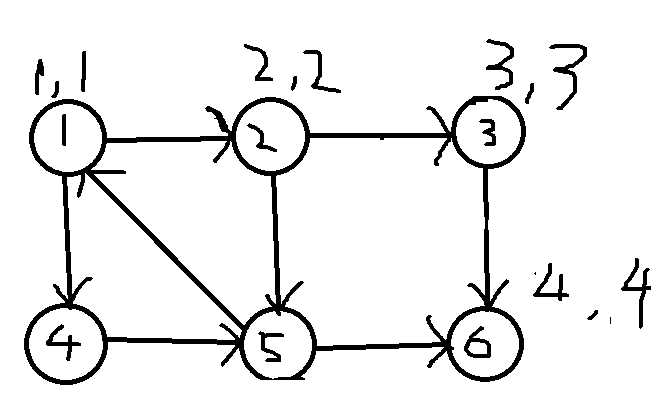
以此类推，将3、6入栈，时间戳分别为3、4

stack：1,2,3,6

此时，发现6节点遍历了其所有出边（本来就没有）以后，它的low等于dfn，这就说明了6号节点没有路径能回到能到达它的节点，所以6就是一个单独的连通分量，因此将6出栈，再回溯，此时在栈中比6（含）高的点都出栈，这些点构成一个连通分量（因为此时比6在栈顶，所以6是一个单独的连通分量）ans++

stack:1,2,3

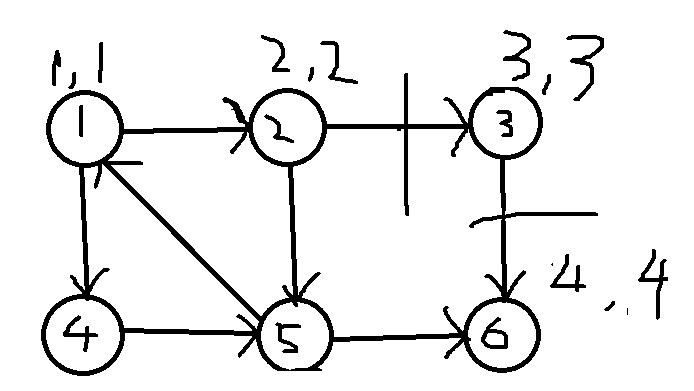
和刚才一样，3节点的所有出边已经遍历一般，但low还是和dfn相等，所以3出栈，因为此时3在栈顶，所以3是一个单独的连通分量。ans++

stack：1,2

再次遍历从2遍历到5，将5入栈，并且low和dfn都为5。

stack：1,2,5

然后5搜索到6，但是6不在栈里面，所以不管它

这是搜索到了1，发现1的时间戳1小于5的low，所以将5的low更新为1,。这时发现5没有其他边可以走了，所以返回

返回到2时，发现5的low比2的low小，所以更新2的low为1，继续返回到1

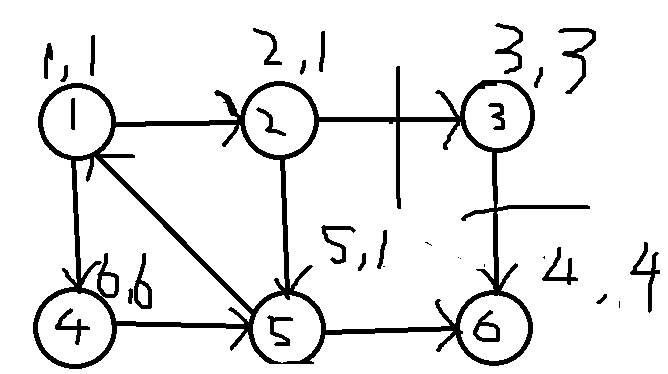
再从1走到4，4的时间戳和low为6，将4入栈

stack：1,2,5,4　　

从4走到5，发现5在栈中，且5的low比4的low小，所以4的low变成1，因为没有边再返回到1

此时，1的所有边都走完啦，并且1的low等于dfn，所以把1及以上的节点出栈，构成连通分量，ans++

继续枚举每一个点，如果这个点的时间戳为0（也就是没有访问过）tarjan(i);

现在贴上代码，但是没有完，我会对原理做详细解释：

void tarjan(int u)
{
    in++;
    dfn[u]=in;
    low[u]=in;
    S.push(u);
    vis[u]=;
    for(int e=head[u];e;e=next[e])
    {
        if(!dfn[to[e]])
        {
            tarjan(to[e]);
            low[u]=min(low[to[e]],low[u]);
        }
        else if(vis[to[e]])
            low[u]=min(low[u],dfn[to[e]]);
    }
    if(low[u]==dfn[u])
    {
        while(!S.empty() && S.top()!=u)
        {
            vis[S.top()]=;
            S.pop();
        }
        vis[u]=;
        S.pop();
        ans++;
    }
} 

演员表：

in:时间戳下标

dfn[i]:i节点的时间戳

low[i]:i所能到达的最小的时间戳

head[i],next[i],to[i]:邻接表群演

vis[i]:i是否在栈里

S：栈

ans:计数

u：当前点

原理详解：

1、其实虽说整个过程都在用栈维护，但是原理却是一颗树，比如当搜索到1、2、3、6时，树是这样的

你想象成树就好，当我们确定6为一个单独的连通分量的时候，把它咔嚓掉。现在6及以下的节点（这次没有）成为一颗新的树。

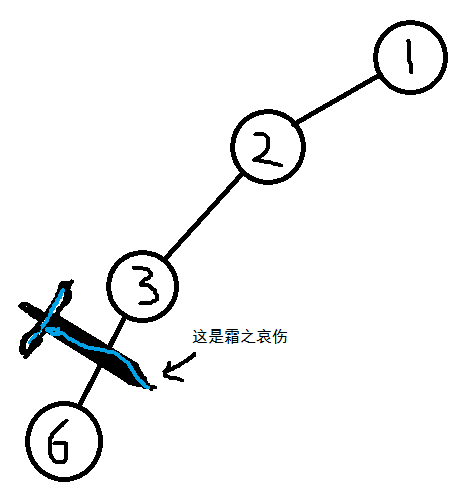
然后再用霜之哀伤砍掉3，3及以下节点（也是没有）又变成了一个新的树。

然后我们搜索到5，将5加入树

然后再从1搜索到4，加入树

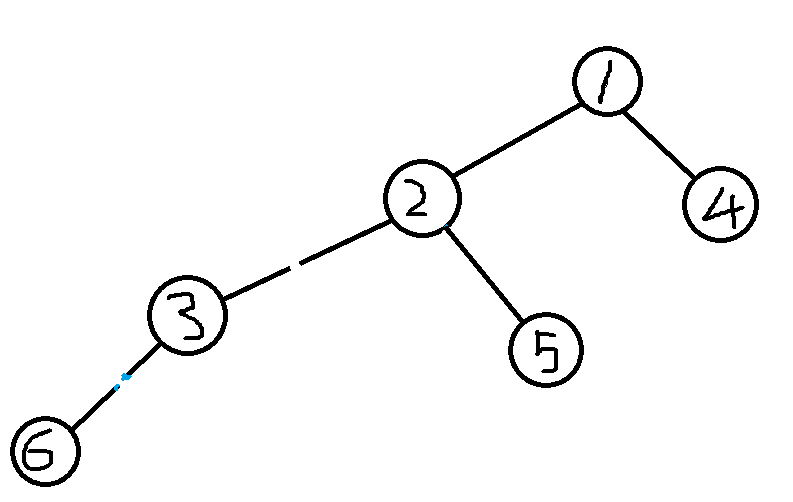
然后返回到1，拔出1节点的霜之哀伤与耐奥祖融合，成为新的巫妖王。

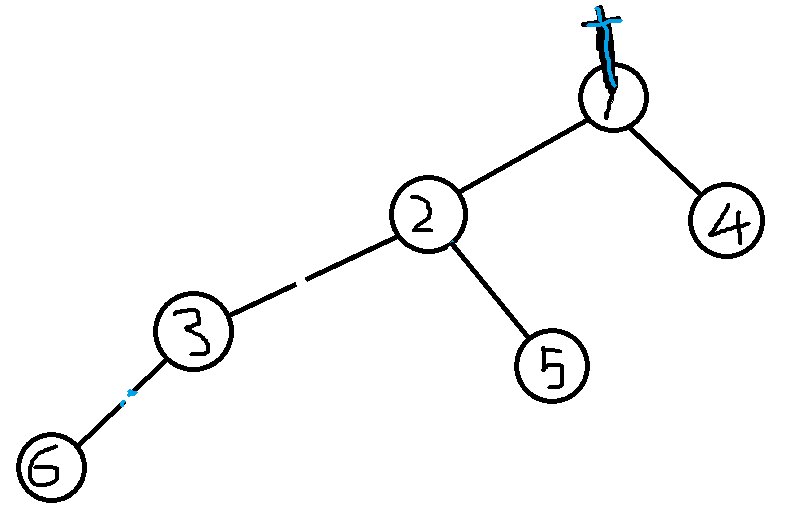
这就是Tarjan的关于连通分量个数的应用了，后续会带来割点割边。