CF459E Pashmak and Graph (DP?
Codeforces Round #261 (Div. 2)
|
E. Pashmak and Graph
time limit per test
1 second memory limit per test
256 megabytes input
standard input output
standard output Pashmak's homework is a problem about graphs. Although he always tries to do his homework completely, he can't solve this problem. As you know, he's really weak at graph theory; so try to help him in solving the problem. You are given a weighted directed graph with n vertices and m edges. You need to find a path (perhaps, non-simple) with maximum number of edges, such that the weights of the edges increase along the path. In other words, each edge of the path must have strictly greater weight than the previous edge in the path. Help Pashmak, print the number of edges in the required path. Input
The first line contains two integers n, m (2 ≤ n ≤ 3·105; 1 ≤ m ≤ min(n·(n - 1), 3·105)). Then, m lines follows. The i-th line contains three space separated integers: ui, vi, wi (1 ≤ ui, vi ≤ n; 1 ≤ wi ≤ 105) which indicates that there's a directed edge with weight wi from vertex ui to vertex vi. It's guaranteed that the graph doesn't contain self-loops and multiple edges. Output
Print a single integer — the answer to the problem. Sample test(s)
Input
3 3 Output
1 Input
3 3 Output
3 Input
6 7 Output
6 Note
In the first sample the maximum trail can be any of this trails: In the second sample the maximum trail is In the third sample the maximum trail is |
大意:给出一个带权有向图,求经过的边权绝对上升的最长路径(可能是非简单路径,即可能经过一个点多次)所包含的边数。
题解:对边按权值排序后,从小到大搞。
设q[x]为已经搞过的边组成的以x点为终点的最长路径包含的边数。
设当前边e[i]为从u到v的边,由于我们是按权值排序好的,只要没有相同的权值,我们就可以q[v]=max(q[v], q[u]+1)。
但是是有相同的权值的,我们直接这样搞,相同权值的可能会连出一条路,是不符合要求的,像第一个样例会输出3,怒萎。
所以相同权值的要特殊搞。我希望相同权值的不是一个个更新,而是一起更新,所以我把相同权值的先不更新,而是压入vector中,统计完这个权值的所有边,再将其一起从vector中取出更新。发现,有些相同权值的边连到的是同一个点,我希望用更长的路来更新这个点,所以对vector排序,后更新更长的。
核心代码如下:
S.push_back( pig(e[].to , ) );
for(i=; i<en; i++) {
if(e[i].w != e[i-].w) {///遇到不同权值的边,则将前一权值的全部边更新
sort(S.begin(),S.end());///使路长的后更新(若有同一个点有多种更新,则会保留路长的)
int maxj=S.size();
for(int j=; j<maxj; j++)
q[S[j].v]=S[j].be;
S.clear();
}
if(q[e[i].to]>=q[e[i].from]+)continue;
S.push_back( pig(e[i].to , q[e[i].from]+) );
}
全代码:
//#pragma comment(linker, "/STACK:102400000,102400000")
#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<queue>
using namespace std;
#define ll long long
#define usll unsigned ll
#define mz(array) memset(array, 0, sizeof(array))
#define minf(array) memset(array, 0x3f, sizeof(array))
#define REP(i,n) for(i=0;i<(n);i++)
#define FOR(i,x,n) for(i=(x);i<=(n);i++)
#define RD(x) scanf("%d",&x)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define WN(x) prllf("%d\n",x);
#define RE freopen("D.in","r",stdin)
#define WE freopen("1biao.out","w",stdout)
#define mp make_pair struct Edge {
int w,from,to,next;
}; Edge e[];
int en;
int q[];
int n,m; struct pig {
int v,be;
pig() {}
pig(int x,int y) {
v=x;
be=y;
}
}; bool operator <(pig x,pig y) {
return x.be<y.be;
} vector<pig>S; void add(int x,int y,int z) {
e[en].w=z;
e[en].to=y;
e[en].from=x;
en++;
} bool cmp(Edge x,Edge y) {
return x.w<y.w;
} int main() {
int i,x,y,z; scanf("%d%d",&n,&m);
en=;
REP(i,m) {
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
} sort(e,e+en,cmp);///边从小到大遍历
int ans=;
memset(q,,sizeof(q)); S.push_back( pig(e[].to , ) );
for(i=; i<en; i++) {
if(e[i].w != e[i-].w) {///遇到不同权值的边,则将前一权值的全部边更新
sort(S.begin(),S.end());///使路长的后更新(若有同一个点有多种更新,则会保留路长的)
int maxj=S.size();
for(int j=; j<maxj; j++)
q[S[j].v]=S[j].be;
S.clear();
}
if(q[e[i].to]>=q[e[i].from]+)continue;
S.push_back( pig(e[i].to , q[e[i].from]+) );
}
sort(S.begin(),S.end());
int maxj=S.size();
for(int j=; j<maxj; j++)
q[S[j].v]=S[j].be; for(i=; i<=n; i++)
ans=max(ans,q[i]);
printf("%d\n",ans);
return ;
}
CF459E Pashmak and Graph (DP?的更多相关文章
- codeforces 459 E. Pashmak and Graph(dp)
题目链接:http://codeforces.com/contest/459/problem/E 题意:给出m条边n个点每条边都有权值问如果两边能够相连的条件是边权值是严格递增的话,最长能接几条边. ...
- Pashmak and Graph(dp + 贪心)
题目链接:http://codeforces.com/contest/459/problem/E 题意:给一个带权有向图, 找出其中最长上升路的长度. 题解:先按权值对所有边排序, 然后依次 u -& ...
- CF459E Pashmak and Graph (Dag dp)
传送门 解题思路 \(dag\)上\(dp\),首先要按照边权排序,然后图都不用建直接\(dp\)就行了.注意边权相等的要一起处理,具体来讲就是要开一个辅助数组\(g[i]\),来避免同层转移. 代码 ...
- cf459E Pashmak and Graph
E. Pashmak and Graph time limit per test 1 second memory limit per test 256 megabytes input standard ...
- codeforces 340D Bubble Sort Graph(dp,LIS)
转载请注明出处: http://www.cnblogs.com/fraud/ ——by fraud Bubble Sort Graph Iahub recently has lea ...
- 【BZOJ-4692】Beautiful Spacing 二分答案 + 乱搞(DP?)
4692: Beautiful Spacing Time Limit: 15 Sec Memory Limit: 128 MBSubmit: 46 Solved: 21[Submit][Statu ...
- [SHOI2001]化工厂装箱员(dp?暴力:暴力)
118号工厂是世界唯一秘密提炼锎的化工厂,由于提炼锎的难度非常高,技术不是十分完善,所以工厂生产的锎成品可能会有3种不同的纯度,A:100%,B:1%,C:0.01%,为了出售方便,必须把不同纯度 ...
- hdu 4747 Mex( 线段树? 不,区间处理就行(dp?))
Mex Time Limit: 15000/5000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)Total Submis ...
- 【BZOJ 1019】 1019: [SHOI2008]汉诺塔 (DP?)
1019: [SHOI2008]汉诺塔 Description 汉诺塔由三根柱子(分别用A B C表示)和n个大小互不相同的空心盘子组成.一开始n个盘子都摞在柱子A上,大的在下面,小的在上面,形成了一 ...
随机推荐
- 【BZOJ-3252】攻略 DFS序 + 线段树 + 贪心
3252: 攻略 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 339 Solved: 130[Submit][Status][Discuss] D ...
- Mac: Jdk版本切换
通过命令’jdk6′, ‘jdk7′,’jdk8′轻松切换到对应的Java版本: 1.首先安装所有的JDk:* Mac自带了的JDK6,安装在目录:/System/Library/Java/JavaV ...
- Zabbix邮件报警-->Script
Version:3.0.1 邮件报警有两种media 1.Email zabbix发送报警邮件到指定smtp服务器(使用系统自带的sendmail,发送邮箱是zabbix服务器的本地邮箱账号) 再由s ...
- HTML5系列三(多媒体播放、本地存储、本地数据库、离线应用)
各浏览器对编码格式的支持情况 audio和video元素的属性介绍 1.src:媒体数据的URL地址 <video src="pr6.mp4"></video&g ...
- struts2文件目录结构
apps 文件夹包含了多个 example 示例应用的压缩包. docs 文件夹包含了 struts 官方的帮助文档. lib 文件夹包含了 struts 提供的类库 jar 包. src 文件夹包含 ...
- Extjs GridPanel用法详解
Extjs GridPanel 提供了非常强大数据表格功能,在GridPanel可以展示数据列表,可以对数据列表进行选择.编辑等.在之前的Extjs MVC开发模式详解中,我们已经使用到了GridPa ...
- WinForm------SplitContainerControl的窗体调用控件方法
Frm_Books窗体(窗体里面有个按钮跳转Frm_Book_Select窗体) private void Add_Book_ItemClick(object sender, DevExpress.X ...
- HTML学习笔记——box
1> HTML写法 <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http: ...
- CSS 中背景图片定位方法
三种: 关键字:background-position: top left; 像素:background-position: 0px 0px; 百分比:background-position: 0% ...
- python的简洁是shell无法代替的
之前线上服务器分发配置都是用shell和expect脚本分发,脚本写了很长,上周换了ansible,现在自己用python写一个,就30行代码就可以实现需求,之前的shell写了快200行了,蛋疼,代 ...

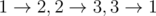 .
. .
.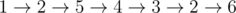 .
.