HDU5739 Fantasia（点双连通分量 + Block Forest Data Structure）

题目

Source

http://acm.hdu.edu.cn/showproblem.php?pid=5739

Description

Professor Zhang has an undirected graph G with n vertices and m edges. Each vertex is attached with a weight wi. Let Gi be the graph after deleting the i-th vertex from graph G. Professor Zhang wants to find the weight of G1,G2,...,Gn.

The weight of a graph G is defined as follows:

1. If G is connected, then the weight of G is the product of the weight of each vertex in G.
2. Otherwise, the weight of G is the sum of the weight of all the connected components of G.

A connected component of an undirected graph G is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices in G.

Input
There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:

The first line contains two integers n and m (2≤n≤10⁵,1≤m≤2×10⁵) -- the number of vertices and the number of edges.

The second line contains n integers w1,w2,...,wn (1≤wi≤10⁹), denoting the weight of each vertex.

In the next m lines, each contains two integers xi and yi (1≤xi,yi≤n,xi≠yi), denoting an undirected edge.

There are at most 1000 test cases and ∑n,∑m≤1.5×10⁶.

Output

For each test case, output an integer $S = (\sum\limits_{i=1}^{n}i\cdot z_i) \text{ mod } (10^9 + 7)$, where zi is the weight of Gi.

Sample Input

1
3 2
1 2 3
1 2
2 3

Sample Output

20

分析

题目大概说给一张无向点带有权无向图。定义连通图的权值为图中各点权的乘积，图的权值为其包含的各连通图的权和。设$z_i$为删除i点后图的权值，求$S = (\sum\limits_{i=1}^{n}i\cdot z_i) \text{ mod } (10^9 + 7)$。

官方题解这么说的：

显然, 只要删掉关键点才会使图不联通. 对于其他点, 权值很容易计算.

首先求出所有的点双联通分量, 对于每一个点双联通分量$S$, 新建一个节点$s$, 向$S$中每个节点$v$连边. 这样一来, 新增的点和原来图中的点会构成一个森林(据说这个有个名字, block forest data structure). 很容易观察到, 叶子节点肯定都是非关键点, 内部节点要么是关键点, 要么是新增的节点.

对于这个森林$F$, 删掉一个关键点或者一个叶子$i$之后, 会得到一个新森林$F_i$​​, 这个$F_i$​​对应的连通块集合和$G_i$对应的连通块集合其实是一样的(不考虑那些新增的点). 显然$G_i$的权值和$F_i$​​的权值也是一样的, $F_i$的权值我们很容易通过树形dp算出来, 那么$G_i$的权值也随之而出.

可以在网上搜到关于用那个BF在线性时间计算所有关节点的影响的论文。。里面有这么一张图：

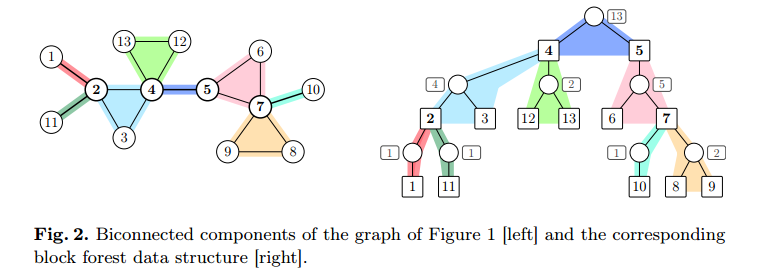
这样就好理解了。

设新加圆形结点的权为1，在那棵构造出来的树中用dp求出各个结点的两个信息：

• pro[u]表示u为根的子树内各个结点权值的乘积
• sum[u]表示Σpro[v]（u为原本图中的结点，v为u的孩子结点）

最后通过枚举要删除的各个点，再加上乘法逆元搞搞，就能直接通过这两个信息很快地求出删除某结点后新的总权值。

另外。。有个地方空间开太小WA了好久。。

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define MAXN 111111
#define MAXM 222222

struct Edge{
    int v,flag,next;
}edge[MAXM<<1];
int NE,head[MAXN];
void addEdge(int u,int v){
    edge[NE].v=v; edge[NE].flag=0; edge[NE].next=head[u];
    head[u]=NE++;
}

struct TEdge{
    int v,next;
}tEdge[MAXM<<4];
int tNE,tHead[MAXN<<1];
void addEdge(int u,int v,int nothing){
    tEdge[tNE].v=v; tEdge[tNE].next=tHead[u];
    tHead[u]=tNE++;
}

int dn,dfn[MAXN],low[MAXN];
int stack[MAXM],top;
int root[MAXN],rn;

void tarjan(int u,int rt){
    dfn[u]=low[u]=++dn;
    for(int i=head[u]; i!=-1; i=edge[i].next){
        if(edge[i].flag) continue;
        edge[i].flag=edge[i^1].flag=1;
        stack[++top]=i;

        int v=edge[i].v;

        if(dfn[v]){
            low[u]=min(low[u],dfn[v]);
            continue;
        }

        tarjan(v,rt);
        low[u]=min(low[u],low[v]);

        if(low[v]>=dfn[u]){
            ++rn;
            int k;
            do{
                k=stack[top--];
                root[edge[k].v]=rt;
                root[edge[k^1].v]=rt;
                addEdge(rn,edge[k].v,0);
                addEdge(edge[k].v,rn,0);
                addEdge(rn,edge[k^1].v,0);
                addEdge(edge[k^1].v,rn,0);
            }while(edge[k^1].v!=u);
        }
    }
}

int n,weight[MAXN];

bool vis[MAXN<<1];
long long sum[MAXN<<1],pro[MAXN<<1];
void dfs(int u){
    vis[u]=1;
    sum[u]=0; pro[u]=(u<=n) ? weight[u] : 1;
    for(int i=tHead[u]; i!=-1; i=tEdge[i].next){
        int v=tEdge[i].v;
        if(vis[v]) continue;
        dfs(v);
        if(u<=n){
            sum[u]+=pro[v];
            sum[u]%=1000000007;
        }
        pro[u]*=pro[v];
        pro[u]%=1000000007;
    }
}

long long ine(long long x){
    long long res=1;
    int n=1000000007-2;
    while(n){
        if(n&1){
            res*=x; res%=1000000007;
        }
        x*=x; x%=1000000007;
        n>>=1;
    }
    return res;
}

int main(){
    int t,m;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        for(int i=1; i<=n; ++i){
            scanf("%d",weight+i);
        }

        NE=0;
        memset(head,-1,sizeof(head));
        int a,b;
        while(m--){
            scanf("%d%d",&a,&b);
            addEdge(a,b);
            addEdge(b,a);
        }

        dn=0; memset(dfn,0,sizeof(dfn));
        rn=n; memset(root,0,sizeof(root));
        top=0;
        tNE=0; memset(tHead,-1,sizeof(tHead));
        for(int i=1; i<=n; ++i){
            if(dfn[i]==0) tarjan(i,rn+1);
        }

        long long tot=0;

        memset(vis,0,sizeof(vis));
        for(int i=1; i<=n; ++i){
            if(vis[i]) continue;
            if(root[i]){
                dfs(root[i]);
                tot+=pro[root[i]];
                tot%=1000000007;
            }else{
                tot+=weight[i];
                tot%=1000000007;
            }
        }

        long long ans=0;

        for(int i=1; i<=n; ++i){
            if(root[i]){
                ans+=(tot-pro[root[i]]+pro[root[i]]*ine(pro[i])%1000000007+sum[i])%1000000007*i;
                ans%=1000000007;
            }else{
                ans+=(tot-weight[i])*i;
                ans%=1000000007;
            }
        }

        if(ans<0) ans+=1000000007;
        printf("%lld\n",ans);
    }
    return 0;
}