codeforces 505B Mr. Kitayuta's Colorful Graph(水题)

转载请注明出处： http://www.cnblogs.com/fraud/          ——by fraud

Mr. Kitayuta's Colorful Graph

Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color c_i, connecting vertex a_i and b_i.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers — u_i and v_i.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex u_i and vertex v_i directly or indirectly.

Input

The first line of the input contains space-separated two integers — n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers — a_i, b_i (1 ≤ a_i < b_i ≤ n) and c_i (1 ≤ c_i ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j, (a_i, b_i, c_i) ≠ (a_j, b_j, c_j).

The next line contains a integer — q (1 ≤ q ≤ 100), denoting the number of the queries.

Then follows q lines, containing space-separated two integers — u_i and v_i (1 ≤ u_i, v_i ≤ n). It is guaranteed that u_i ≠ v_i.

Output

For each query, print the answer in a separate line.

Sample test(s)

Input

4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4

Output

2
1
0

Input

5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4

Output

1
1
1
1
2

Note

Let's consider the first sample.

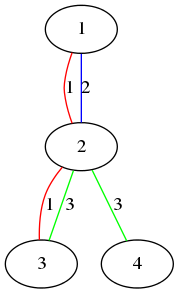The figure above shows the first sample.

• Vertex 1 and vertex 2 are connected by color 1 and 2.
• Vertex 3 and vertex 4 are connected by color 3.
• Vertex 1 and vertex 4 are not connected by any single color.

并查集，暴力都可以过，大水题

 #include <iostream>
 using namespace std;
 #define MAXN 110
 int pa[][],ra[][];
 void init()
 {
     for(int i=;i<MAXN;i++)
     {
         for(int j=;j<MAXN;j++){
             pa[i][j]=j;
             ra[i][j]=;
         }
     }
 }
 int find(int x,int c){
     if(pa[c][x]!=x)pa[c][x]=find(pa[c][x],c);
     return pa[c][x];
 }
 int unite(int x,int y,int c){
     x=find(x,c);
     y=find(y,c);
     if(x==y)return ;
     if(ra[c][x]<ra[c][y])
     {
         pa[c][x]=y;
     }else{
         pa[c][y]=x;
         if(ra[c][x]==ra[c][y])ra[c][x]++;
     }
     return ;
 }
 bool same(int x,int y,int c){
     return find(x,c)==find(y,c);
 }

 int main()
 {
     ios::sync_with_stdio(false);
     int n,m;
     init();
     cin>>n>>m;
     int u,v,c;
     for(int i=;i<m;i++){
         cin>>u>>v>>c;
         u--,v--,c--;
         unite(u,v,c);
     }
     int q;
     cin>>q;
     for(int i=;i<q;i++){
         cin>>u>>v;
         u--;v--;
         int ans=;
         for(int i=;i<m;i++)
         {
             if(same(u,v,i))ans++;
         }
         cout<<ans<<endl;
     }

     return ;
 }

代码君