bzoj3995[SDOI2015]道路修建
http://www.lydsy.com/JudgeOnline/problem.php?id=3995
线段树维护连通性。
我们发现,对于一个区间[L,R],我们只需要知道(1,L),(2,L),(1,R)和(2,R)这4个点的之间的连通情况即可。
我们在线段树中,假设当前节点的表示的区间的为[L,R],我们需要知道(1,L),(2,L),(1,R)和(2,R)这4个点的之间的连通情况,但是为了方便,我们记了(1,L),(2,L),(1,R+1)和(2,R+1)这4个点的连通情况。
每个节点记住5种连通情况:
1:
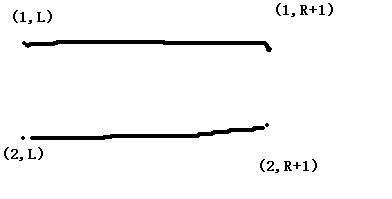
2:

3:
 或
或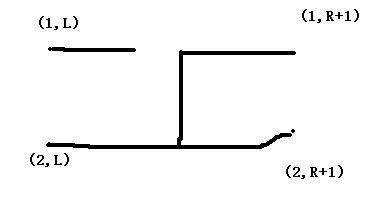
4:
 或
或
5:
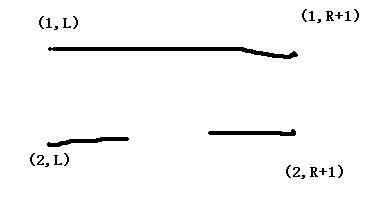 或
或
这样分类的好处是合并的时候比较简单。
合并的时候只有17种是合法的,一一打表即可。
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<fstream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<utility>
#include<set>
#include<bitset>
#include<vector>
#include<functional>
#include<deque>
#include<cctype>
#include<climits>
#include<complex>
//#include<bits/stdc++.h>适用于CF,UOJ,但不适用于poj using namespace std; typedef long long LL;
typedef double DB;
typedef pair<int,int> PII;
typedef complex<DB> CP; #define mmst(a,v) memset(a,v,sizeof(a))
#define mmcy(a,b) memcpy(a,b,sizeof(a))
#define fill(a,l,r,v) fill(a+l,a+r+1,v)
#define re(i,a,b) for(i=(a);i<=(b);i++)
#define red(i,a,b) for(i=(a);i>=(b);i--)
#define ire(i,x) for(typedef(x.begin()) i=x.begin();i!=x.end();i++)
#define fi first
#define se second
#define m_p(a,b) make_pair(a,b)
#define p_b(a) push_back(a)
#define SF scanf
#define PF printf
#define two(k) (1<<(k)) template<class T>inline T sqr(T x){return x*x;}
template<class T>inline void upmin(T &t,T tmp){if(t>tmp)t=tmp;}
template<class T>inline void upmax(T &t,T tmp){if(t<tmp)t=tmp;} inline int sgn(DB x){if(abs(x)<1e-)return ;return(x>)?:-;}
const DB Pi=acos(-1.0); int gint()
{
int res=;bool neg=;char z;
for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar());
if(z==EOF)return ;
if(z=='-'){neg=;z=getchar();}
for(;z!=EOF && isdigit(z);res=res*+z-'',z=getchar());
return (neg)?-res:res;
}
LL gll()
{
LL res=;bool neg=;char z;
for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar());
if(z==EOF)return ;
if(z=='-'){neg=;z=getchar();}
for(;z!=EOF && isdigit(z);res=res*+z-'',z=getchar());
return (neg)?-res:res;
} const int maxN=;
const int INF=0x3f3f3f3f; int N,Q;
int A[maxN+][]; struct Tnode
{
int X[];
int& operator [](int i){return X[i];}
}; const int magic[][]=
{
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
{,,},
}; Tnode operator +(Tnode L,Tnode R)
{
int i;Tnode res;
mmst(res.X,0x3f);
re(i,,-)upmin(res[magic[i][]],L[magic[i][]]+R[magic[i][]]);
return res;
} Tnode T[*maxN+]; Tnode calc(int s)
{
Tnode res;
res[]=A[s][]+A[s][];
res[]=A[s][]+A[s][]+A[s][]+A[s+][]-max(max(A[s][],A[s][]),max(A[s][],A[s+][]));
res[]=A[s+][]+min(A[s][],A[s][]);
res[]=A[s][]+min(A[s][],A[s][]);
res[]=min(A[s][],A[s][]);
return res;
} void build(int rt,int l,int r)
{
if(l==r){T[rt]=calc(l);return;}
int mid=(l+r)>>;
build(rt<<,l,mid);
build(rt<<|,mid+,r);
T[rt]=T[rt<<]+T[rt<<|];
} void change(int rt,int l,int r,int x)
{
if(l==r){T[rt]=calc(l);return;}
int mid=(l+r)>>;
if(x<=mid) change(rt<<,l,mid,x); else change(rt<<|,mid+,r,x);
T[rt]=T[rt<<]+T[rt<<|];
} Tnode ask(int rt,int l,int r,int x,int y)
{
if(x<=l && r<=y) return T[rt];
int mid=(l+r)>>;
if(y<=mid) return ask(rt<<,l,mid,x,y);
if(mid+<=x) return ask(rt<<|,mid+,r,x,y);
return ask(rt<<,l,mid,x,y)+ask(rt<<|,mid+,r,x,y);
} int main()
{
freopen("road.in","r",stdin);
freopen("road.out","w",stdout);
int i;
N=gint();Q=gint();
re(i,,N-)A[i][]=gint();
re(i,,N-)A[i][]=gint();
re(i,,N)A[i][]=gint();
build(,,N-);
while(Q--)
{
char type=getchar();while(type!='C' && type!='Q')type=getchar();
if(type=='C')
{
int x0=gint(),y0=gint(),x1=gint(),y1=gint(),w=gint();
if(x0==x1)
{
A[min(y0,y1)][x0]=w;
change(,,N-,min(y0,y1));
}
else
{
A[y0][]=w;
if(y0!=)change(,,N-,y0-);
if(y0!=N)change(,,N-,y0);
}
}
else
{
int l=gint(),r=gint();
if(l==r)
PF("%d\n",A[l][]);
else
{
Tnode ans=ask(,,N-,l,r-);
PF("%d\n",ans[]);
}
}
}
return ;
}
bzoj3995[SDOI2015]道路修建的更多相关文章
- 【线段树】bzoj3995 [SDOI2015]道路修建
线段树每个结点维护5个域: 整个区间的MST. 将两个左端点连通,两个右端点不连通,整个区间内选择2*(r-l+1)-2条边的最小生成森林,有两个连通块. 将两个右端点连通,两个左端点不连通,整个区间 ...
- [bzoj3995] [SDOI2015]道路修建 线段树
Description 某国有2N个城市,这2N个城市构成了一个2行N列的方格网.现在该国政府有一个旅游发展计划,这个计划需要选定L.R两列(L<=R),修建若干条专用道路,使得这两列之间(包括 ...
- 【BZOJ3995】[SDOI2015]道路修建 线段树区间合并
[BZOJ3995][SDOI2015]道路修建 Description 某国有2N个城市,这2N个城市构成了一个2行N列的方格网.现在该国政府有一个旅游发展计划,这个计划需要选定L.R两列(L&l ...
- [BZOJ 3995] [SDOI2015] 道路修建 【线段树维护连通性】
题目链接:BZOJ - 3995 题目分析 这道题..是我悲伤的回忆.. 线段树维护连通性,与 BZOJ-1018 类似,然而我省选之前并没有做过 1018,即使它在 ProblemSet 的第一页 ...
- [SDOI2015]道路修建(线段树)
题意:给定2行n列的四连通带权网格图,支持修改边权和查询第[l,r]列的最小生成树 题解:这是一道好题,要么SDOI2019中n=2的20pts怎么会“我抄我自己”?(当然NOIP2018“我抄我自己 ...
- 【BZOJ-2435】道路修建 (树形DP?)DFS
2435: [Noi2011]道路修建 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 3115 Solved: 1002[Submit][Statu ...
- 【bzoj2435】[NOI2011]道路修建
题目描述 在 W 星球上有 n 个国家.为了各自国家的经济发展,他们决定在各个国家之间建设双向道路使得国家之间连通.但是每个国家的国王都很吝啬,他们只愿意修建恰好 n – 1条双向道路. 每条道路的修 ...
- 【NOI2011】道路修建 BFS
[NOI2011]道路修建 Description 在 W 星球上有 n 个国家.为了各自国家的经济发展,他们决定在各个国家之间建设双向道路使得国家之间连通.但是每个国家的国王都很吝啬,他们只愿意修建 ...
- 【BZOJ】2435: [Noi2011]道路修建(树形dp)
http://www.lydsy.com/JudgeOnline/problem.php?id=2435 我怎么感觉那么水.. 坑的是,dfs会爆...好吧..用bfs.. //upd:我的智商也是醉 ...
随机推荐
- C#3.0 语言基础扩充
隐含类型局部变量 var i = 5; var h = 13.4; var s = "C Sharp"; var intArr = new[] {1,2,3 }; var a = ...
- JPush 极光推送 消息推送 实例
简介 官网:https://www.jpush.cn/ 极光推送(JPush)是一个端到端的推送服务,使得服务器端消息能够及时地推送到终端用户手机上,让开发者积极地保持与用户的连接,从而提高用户活跃度 ...
- ARGB和RGB
ARGB 一种色彩模式,也就是RGB色彩模式附加上Alpha(透明度)通道,常见于32位位图的存储结构. ARGB---Alpha,Red,Green,Blue. Alpha-图像通道 如果图形卡具有 ...
- 网页上facebook分享功能的具体实现
1,一个链接: 参数是要分享的页面的链接 代码如下: <a style="width:35px; height:40px; position:relative; top:10px; l ...
- WCF理论 【转载】
原文地址:http://blog.itpub.net/23109131/viewspace-661613/ WCF是什么? WCF是"Windows Communication Founda ...
- FAL[client]: Failed to request gap sequence GAP - thread 1 sequence 29-29
一:问题描述 主备库所在机器都重启后,rac(主库)开机自动启动,但备库(单实例)不是开机启动,现已手工启动到mount,并已在备库上alter database recover standby d ...
- 武汉科技大学ACM :1008: 华科版C语言程序设计教程(第二版)习题6.14
Problem Description 输入一个八进制的字符串,将它转换成等价的十进制字符串,用pringf的%s格式输出. Input 首先输入一个正整数t,表示有t组测试数据(1<= t & ...
- EIGRP认证 配置 (仅仅是命令 原理自己去看书) 转自:http://blog.163.com/s_u/blog/static/13308367201111771831631/
EIGRP认证 目的:掌握EIGRP的MD5认证 拓扑:这里IP配置我就不写出来了,应该对大家来说是非常简单的事了,就要细心一点就可以了.首先我们在R1上启用MD5认证R1(config)#key c ...
- SSM框架搭建java.lang.ClassNotFoundException: org.springframework.http.converter.json.MappingJacksonHttpMessageConverter
在搭建 spring springMVC Mybatis 时候出错 将org.springframework.http.converter.json.MappingJacksonHttpMessage ...
- JS判断字符串是否为空、过滤空格、查找字符串位置等函数集
这是一个由网上收集的JS代码段,用于判断指定字符串是否为空,过滤字符串中某字符两边的空格.查找指定字符串开始的位置.使用IsFloat函数判断一 个字符串是否由数字(int or long or fl ...
