关于KMP算法理解（快速字符串匹配）

参考：http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

2016-08-22

前言：自己看《算法导论》中关于KMP算法的讲解，文字描述+插图+伪代码，但最终还是云里雾里。之后借助于上面提到的博客才有所体会。感谢博主。

对于其最核心的部分---当模板字符串中前面q个字符和源字符串中的某个子串匹配时，如果继续往下匹配，发现两个字符并不相同，那该如何移动模板字符串进行比较呢？

1. 最简单的方法当然是，将模板字符串向后移动一位，继续从头开始比较每一个字符。很明显，这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。

2. 就是利用KMP算法，设法利用前面已经比较过的q位字符串信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。

那么KMP算法的移动方法是什么呢？

答案是：借助一个next数组（也称为部分匹配表）来计算下次字符串移动的位数应该是多少。

如下图所示：

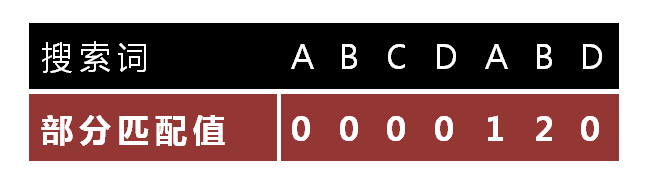
下面介绍部分匹配表是如何产生的：

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，（这只是相对于模板字符串而言，与源字符串无关）

首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

例如：

－　"A"的前缀和后缀都为空集，共有元素的长度为0；         q=1

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；              q=2

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；          q=3

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；   q=4

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；   q=5

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；    q=6

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。  q=7

最后，模板字符串移动的位数 = q - 部分匹配值。（其中q表示已经匹配的字符的个数。）

" 部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长 度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度（q) - 部分匹配值），就可以来到第二个"AB"的位置。

所以，通过避免一些不必要的比较，这样就可以提高算法效率，时间复杂度为O(m+n)，而一般方法复杂度为O(m×n)。

算法理解，到此就清楚了，实现代码如下：

简单匹配算法的时间复杂度为O(m*n)，KMP匹配算法，可以证明它的时间复杂度为O(m+n).。

一.简单匹配算法