51Nod 快速傅里叶变换题集选刷
打开51Nod全部问题页面,在右边题目分类中找到快速傅里叶变换,然后按分值排序,就是本文的题目顺序。
1.大数乘法问题
这个……板子就算了吧。
2.美妙的序列问题
长度为n的排列,且满足从中间任意位置划分为两个非空数列后,左边的最大值>右边的最小值。问这样的排列有多少个%998244353。
多组询问,n,T<=100000。
题解:经过分析可知,不合法的排列一定存在这样一种划分:
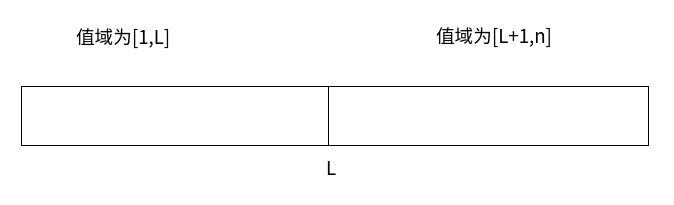
我们考虑答案=f[i]=i!-不合法排列个数。
形如 2 1 3 4 6 5 这种排列,会有三种划分方式不合法(1 | 3,3 | 4,4 | 6),直接算阶乘会计算重复。
而我们又发现,后两种划分,左边的子串仍是一个不合法的排列(显然)。
于是我们强制要求左边的排列是一个合法的排列,即在最左边统计贡献,这样就可以不重不漏了。
得到递推式显然:
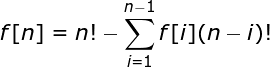
分治NTT即可,预处理后O(1)回答。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <map>
#include <set>
#define LL long long
#define FILE "美妙的序列"
using namespace std; const int N = ;
const int Mod = ;
const int G = ;
int f[N],rev[N],L,Jc[N],a[N],b[N]; inline int gi(){
int x=,res=;char ch=getchar();
while(ch>'' || ch<'')res^=ch=='-',ch=getchar();
while(ch>=''&&ch<='')x=x*+ch-,ch=getchar();
return res?x:-x;
} inline int QPow(int d,int z,int ans=){
for(;z;z>>=,d=1ll*d*d%Mod)
if(z&)ans=1ll*ans*d%Mod;
return ans;
} inline void NTT(int *A,int n,int f){
for(int i=;i<n;++i)
if(i<rev[i])swap(A[i],A[rev[i]]);
for(int i=;i<n;i<<=){
int z=f*(Mod-)/(i<<),gn=QPow(G,(z+Mod-)%(Mod-));
for(int j=;j<n;j+=i<<){
int g=,x,y;
for(int k=;k<i;++k,g=1ll*g*gn%Mod){
x=A[j+k];y=1ll*g*A[i+j+k]%Mod;
A[j+k]=(x+y)%Mod;A[i+j+k]=(x-y+Mod)%Mod;
}
}
}
if(f==)return;int iv=QPow(n,Mod-);
for(int i=;i<n;++i)A[i]=1ll*A[i]*iv%Mod;
} inline void solve(int l,int r){
if(l==r){f[l]=(Jc[l]-f[l]%Mod+Mod)%Mod;return;}
int mid=(l+r)>>;
solve(l,mid);
int n,m=r-l+;L=;
for(n=;n<=m;n<<=)L++;
for(int i=;i<n;++i)
rev[i]=(rev[i/]/)|((i&)<<(L-)); for(int i=;i<n;++i)a[i]=b[i]=;
for(int i=l;i<=mid;++i)a[i-l]=f[i];
for(int i=;i<m;++i)b[i]=Jc[i];
NTT(a,n,);NTT(b,n,);
for(int i=;i<n;++i)a[i]=1ll*a[i]*b[i]%Mod;
NTT(a,n,-);
for(int i=mid+;i<=r;++i)f[i]=(f[i]+a[i-l])%Mod;
solve(mid+,r);
} int main(){
//freopen(FILE".in","r",stdin);
//freopen(FILE".out","w",stdout);
int Case=gi();Jc[]=;
for(int i=;i<=;++i)
Jc[i]=1ll*Jc[i-]*i%Mod;
solve(,);
while(Case--)printf("%d\n",f[gi()]);
fclose(stdin);fclose(stdout);
return ;
}
美妙的序列
3.哈希统计问题
给定base,p,求经过经典哈希(ans=(ans*base+a[i])%p;)后哈希值=x的长度<=n的小写字符串个数%998244353,n,p,base<=50000。
题解:对于长度<=n的问题先不考虑,先考虑恰好为n的。
设f[i][j]为已有i个字母,哈希值为j的串个数,则转移为: f[i][j] -> f[i+1][(j*base+Ascll[c])%p]。
如果把j*base看成模p意义下的j',显然转移是一个多项式相乘形式。
常见的套路是:观察当i为偶数时,f[i/2]是否能直接推出f[i]。
显然可以,j*base变成j*basei/2就可以了。写出来是一个卷积的形式,一遍NTT即可。
于是直接暴力递归,i为奇数则化为f[i-1]*f[1]继续暴力,只会做O(log)次。
现在要求<=n的,那么同样设pre[i][j]为已有<=i个字母,哈希值为j的串的个数。
转移:pre[i]*f[j]+pre[j] -> pre[i+j]。
即:选[j+1,i+j]个的和选[1,j]的方案数相加,就是选[1,i+j]个的个数。
剩下的就是一点细节,调试一会儿应该也很好写出来。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <map>
#include <set>
#define LL long long
#define FILE "哈希统计"
using namespace std; const int N = ;
const int M = ;
const int Mod = ;
const int G = ;
int p,Bs,m,wx;
int idf,idpre,f[M][N],pre[M][N],f_vis[N],pre_vis[N];
int n,rev[N],L,a[N],b[N]; inline int gi(){
int x=,res=;char ch=getchar();
while(ch>'' || ch<'')res^=ch=='-',ch=getchar();
while(ch>=''&&ch<='')x=x*+ch-,ch=getchar();
return res?x:-x;
} inline int QPow(int d,int z,int Mod,int ans=){
for(;z;z>>=,d=1ll*d*d%Mod)
if(z&)ans=1ll*ans*d%Mod;
return ans;
} inline void NTT(int *A,int f){
for(int i=;i<n;++i)
if(i<rev[i])swap(A[i],A[rev[i]]);
for(int i=;i<n;i<<=){
int z=f*(Mod-)/(i<<),gn=QPow(G,(z+Mod-)%(Mod-),Mod);
for(int j=;j<n;j+=i<<){
int g=,x,y;
for(int k=;k<i;++k,g=1ll*g*gn%Mod){
x=A[j+k];y=1ll*g*A[i+j+k]%Mod;
A[j+k]=(x+y)%Mod;A[i+j+k]=(x-y+Mod)%Mod;
}
}
}
if(f==)return;int iv=QPow(n,Mod-,Mod);
for(int i=;i<n;++i)A[i]=1ll*A[i]*iv%Mod;
} inline void Mul(int *H,int *g,int *h){
NTT(g,);NTT(h,);
for(int i=;i<n;++i)
H[i]=1ll*g[i]*h[i]%Mod;
NTT(H,-);
for(int i=n-;i>=p;--i)
H[i-p]=(H[i-p]+H[i])%Mod,H[i]=;
} inline int getf(int x){
if(f_vis[x])return f_vis[x];
if(x==){
++idf;
for(int i='a';i<='z';++i)
f[idf][i%p]++;
return idf;
}
int id0,id1,len0,len1,pw;
if(x&)id0=getf(len0=x-),id1=getf(len1=);
else id0=id1=getf(len0=len1=x/);
++idf;pw=QPow(Bs,len1,p); for(int i=;i<n;++i)a[i]=,b[i]=f[id1][i];
for(int i=;i<p;++i)
if(f[id0][i]){
int y=1ll*i*pw%p;
a[y]=(a[y]+f[id0][i])%Mod;
}
Mul(f[idf],a,b);
return f_vis[x]=idf;
} inline int getpre(int x){
if(pre_vis[x])return pre_vis[x];
if(x==){
++idpre;int id=getf(x);
for(int i=;i<n;++i)
pre[idpre][i]=f[id][i];
return idpre;
}
int id0,id1,id2,len0,len1,pw;
if(x&)id0=getpre(len0=x-),id1=getf(len1=);
else id0=getpre(len0=x/),id1=getf(len1=x/);
id2=getpre(len1);pw=QPow(Bs,len1,p);++idpre; for(int i=;i<n;++i)a[i]=,b[i]=f[id1][i];
for(int i=;i<p;++i)
if(pre[id0][i]){
int y=1ll*i*pw%p;
a[y]=(a[y]+pre[id0][i])%Mod;
}
Mul(pre[idpre],a,b);
for(int i=;i<p;++i)
pre[idpre][i]=(pre[idpre][i]+pre[id2][i])%Mod;
return pre_vis[x]=idpre;
} int main(){
//freopen(FILE".in","r",stdin);
//freopen(FILE".out","w",stdout);
m=gi();Bs=gi();p=gi();wx=gi();
for(n=;n<p+p;n<<=)L++;
for(int i=;i<n;++i)
rev[i]=(rev[i/]/)|((i&)<<(L-));
int id=getpre(m);
printf("%d\n",pre[id][wx]);
fclose(stdin);fclose(stdout);
return ;
}
哈希统计
4.乘积之和
给定正整数序列序列A[1...n],有Q次询问,每次询问给出k,在A中任选k个数可以得到一个乘积。求所有方案的乘积的总和%100003。n,Q<=50000。
题解:暴力DP很显然,设f[i][j]表示前i个数选j个数的乘积和,那么可以直接转移f[i][j] -> f[i+1][j*A[i+1]%100003]。
用上面那题的套路,f[i/2]是否能推出f[i]?仔细分析后发现是可以的。
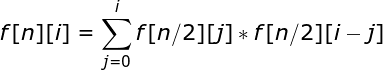
发现这也是一个卷积形式!但是这题是有多组询问的,不能直接暴力递归求。
分治•NTT,solve(l,r)表示得到在A[l...r]中选k个的乘积和数组,总复杂度O(nlog2n),最后求出所有解。
因为不是费马质数,卷积上界又只有10^14级别,两个费马质数用中国剩余定理合并一下就可以了。
upd:用母函数来理解可能更好。
易推出我们求的是多项式

在xk项的系数。同样的,上式可用分治法,合并时使用NTT,代码是一样的。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <map>
#include <set>
#define LL long long
#define FILE "乘积之和"
using namespace std; const LL N = ;
const LL M = ;
const LL G = ;
LL Q,A[N];
LL f[][N],rev[N];
LL P[]={,}; inline LL gi(){
LL x=,res=;char ch=getchar();
while(ch>'' || ch<'')res^=ch=='-',ch=getchar();
while(ch>=''&&ch<='')x=x*+ch-,ch=getchar();
return res?x:-x;
} inline LL Mul(LL a,LL b,LL Mod,LL ans=){
if(Mod<=P[])return a*b%Mod;
for(;b;b>>=,a=(a+a)%Mod)
if(b&)ans=(ans+a)%Mod;
return ans;
} inline LL QPow(LL d,LL z,LL Mod,LL ans=){
for(d=d%Mod,z=z%Mod;z;z>>=,d=d*d%Mod)
if(z&)ans=ans*d%Mod;
return ans;
} inline void NTT(LL *A,LL n,LL f,LL Mod){
for(LL i=;i<n;++i)
if(i<rev[i])swap(A[i],A[rev[i]]);
for(LL i=;i<n;i<<=){
LL z=f*(Mod-)/(i<<),gn=QPow(G,(z+Mod-)%(Mod-),Mod);
for(LL j=;j<n;j+=i<<){
LL g=,x,y;
for(LL k=;k<i;k++,g=1ll*g*gn%Mod){
x=A[j+k];y=1ll*g*A[i+j+k]%Mod;
A[j+k]=(x+y)%Mod;A[i+j+k]=(x-y+Mod)%Mod;
}
}
}
if(f==)return;LL iv=QPow(n,Mod-,Mod);
for(LL i=;i<n;++i)A[i]=1ll*A[i]*iv%Mod;
} inline LL CRT(LL r0,LL r1){
LL Mod=1ll*P[]*P[];
LL v0=QPow(P[],P[]-,P[]),v1=QPow(P[],P[]-,P[]);
LL r=(Mul(v0*P[]%Mod,r0,Mod)+Mul(v1*P[]%Mod,r1,Mod))%Mod;
return r%M;
} inline void solve(LL l,LL r,LL dep){
if(l==r){
f[dep][]=;f[dep][]=A[l]%M;
return;
}
LL mid=(l+r)>>;
LL m=r-l+,n=,L=;
for(;n<=m;n<<=)L++; LL a[][n+],b[][n+]; solve(l,mid,dep+);
for(LL i=;i<=mid-l+;++i)a[][i]=a[][i]=f[dep+][i];
for(LL i=mid-l+;i<n;++i)a[][i]=a[][i]=; solve(mid+,r,dep+);
for(LL i=;i<=r-mid;++i)b[][i]=b[][i]=f[dep+][i];
for(LL i=r-mid+;i<n;++i)b[][i]=b[][i]=; for(LL i=;i<n;++i)
rev[i]=(rev[i/]/)|((i&)<<(L-)); for(LL t=;t<;++t){
NTT(a[t],n,,P[t]);NTT(b[t],n,,P[t]);
for(LL i=;i<n;++i)a[t][i]=1ll*a[t][i]*b[t][i]%P[t];
NTT(a[t],n,-,P[t]);
} for(LL i=;i<=m;++i)
f[dep][i]=CRT(a[][i],a[][i]); } int main(){
LL n=gi();Q=gi();
for(LL i=;i<=n;++i)A[i]=gi();
solve(,n,);
for(LL t=;t<=Q;++t)
printf("%lld\n",f[][gi()]);
fclose(stdin);fclose(stdout);
return ;
}
乘积之和
5.模糊搜索问题
题意:给定两个串A,B,字符集大小为4,匹配规则是若A[j-k]~A[j+k]中存在B[i]则算B[i]在A[j]出现,求B在A中出现了多少次,长度<=100000。
比如说k=2的情况。
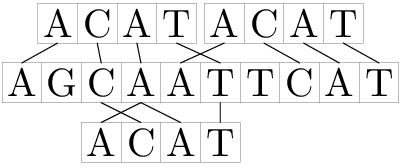
题解:这种字符串问题用FFT来做的套路似乎都和万径人踪灭差不多?
首先那个k的限制可以用两遍扫+差分搞定出字符c在A[i]出是否算的上出现,记为g[c][i]。
B在A[i]处开头,则对于'A'、'T'、'C'、‘G’,,有如下式子:
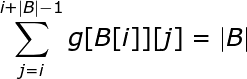
这样仍不好做,把式子构造一下:
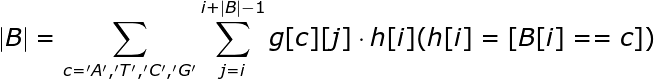
这就形成了多项式乘法的形式,跑四遍就可以了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <map>
#include <set>
#define LL long long
#define FILE "模糊搜索"
using namespace std; const int N = ;
const double pi = acos(-1.0);
int S,T,K,n,m,L,rev[N],ID[],cf[N],num[][N],Ans;
struct dob{
double real,imag;
dob(){};
dob(double _r,double _i){real=_r;imag=_i;}
dob operator +(const dob &a)const{
return (dob){real+a.real,imag+a.imag};
}
dob operator -(const dob &a)const{
return (dob){real-a.real,imag-a.imag};
}
dob operator *(const dob &a)const{
double r=real*a.real-imag*a.imag;
double i=real*a.imag+imag*a.real;
return (dob){r,i};
}
}a[N],b[N],f[][N];
char s[N],t[N]; inline int gi(){
int x=,res=;char ch=getchar();
while(ch>''||ch<''){if(ch=='-')res*=-;ch=getchar();}
while(ch<=''&&ch>='')x=x*+ch-,ch=getchar();
return x*res;
} inline void FFT(dob *A,int f){
for(int i=;i<n;++i)
if(i<rev[i])swap(A[i],A[rev[i]]);
for(int i=;i<n;i<<=){
dob wn(cos(pi/i),sin(f*pi/i)),x,y;
for(int j=;j<n;j+=i<<){
dob w(,);
for(int k=;k<i;k++,w=w*wn){
x=A[j+k];y=w*A[i+j+k];
A[j+k]=x+y;A[i+j+k]=x-y;
}
}
}
if(f==)return;
for(int i=;i<n;++i)
A[i].real=int(A[i].real/n+0.5);
} inline void work(char ch,int sum=){
for(int i=;i<n;++i)cf[i]=;
for(int i=;i<=S;++i)
if(s[i]==ch){
cf[max(,i-K)]++;
cf[min(n+,i+K+)]--;
}
for(int i=;i<n;++i)cf[i]+=cf[i-];
for(int i=;i<=S;++i)
a[i].real=cf[i]>,a[i].imag=;
for(int i=S+;i<n;++i)
a[i].real=a[i].imag=;
for(int i=;i<=T;++i)
sum+=b[i].real=t[i]==ch,b[i].imag=;
for(int i=T+;i<n;++i)
b[i].real=b[i].imag=;
reverse(b+,b+T+);
FFT(a,);FFT(b,);
for(int i=,id=ID[ch];i<n;++i)
f[id][i]=a[i]*b[i];
FFT(f[ID[ch]],-);
for(int i=;i<=S;++i)
num[ID[ch]][i]=sum==int(f[ID[ch]][i+T].real+0.001);
} int main(){
//freopen(FILE".in","r",stdin);
//freopen(FILE".out","w",stdout);
S=gi();T=gi();K=gi();
for(n=,m=S+T;n<m;n<<=)L++;
for(int i=;i<n;++i)
rev[i]=(rev[i/]/)|((i&)<<(L-));
ID['A']=;ID['T']=;ID['C']=;ID['G']=;
scanf("%s%s",s+,t+);
work('A');work('T');work('C');work('G');
for(int i=;i<=S;++i)
if(num[][i] && num[][i] && num[][i] && num[][i])
Ans++;
printf("%d\n",Ans);
fclose(stdin);fclose(stdout);
return ;
}
模糊搜索问题
51Nod 快速傅里叶变换题集选刷的更多相关文章
- 51nod 贪心算法题集
2070 最小罚款: 题意:初始有n元,每个任务有2个参数:t和w,<=t时刻前完成任务才可避免造成损失w.问:如何安排才能尽可能避免损失?一个任务执行时间是一个单位时间. 分析:任务按时间排个 ...
- 多项式 之 快速傅里叶变换(FFT)/数论变换(NTT)/常用套路【入门】
原文链接https://www.cnblogs.com/zhouzhendong/p/Fast-Fourier-Transform.html 多项式 之 快速傅里叶变换(FFT)/数论变换(NTT)/ ...
- 快速傅里叶变换(FFT)学习笔记(未完待续)
目录 参考资料 FFT 吹水 例题 普通做法 更高大尚的做法 定义与一部分性质 系数表达式 点值表达式 点值相乘??? 卷积 复数 单位根 DFT IDFT 蝴蝶迭代优化 单位根求法 实现.细节与小优 ...
- 【笔记篇】(理论向)快速傅里叶变换(FFT)学习笔记w
现在真是一碰电脑就很颓废啊... 于是早晨把电脑锁上然后在旁边啃了一节课多的算导, 把FFT的基本原理整明白了.. 但是我并不觉得自己能讲明白... Fast Fourier Transformati ...
- Algorithm: 多项式乘法 Polynomial Multiplication: 快速傅里叶变换 FFT / 快速数论变换 NTT
Intro: 本篇博客将会从朴素乘法讲起,经过分治乘法,到达FFT和NTT 旨在能够让读者(也让自己)充分理解其思想 模板题入口:洛谷 P3803 [模板]多项式乘法(FFT) 朴素乘法 约定:两个多 ...
- 【数学】快速傅里叶变换(FFT)
快速傅里叶变换(FFT) FFT 是之前学的,现在过了比较久的时间,终于打算在回顾的时候系统地整理一篇笔记,有写错的部分请指出来啊 qwq. 卷积 卷积.旋积或褶积(英语:Convolution)是通 ...
- 浅谈FFT(快速傅里叶变换)
前言 啊摸鱼真爽哈哈哈哈哈哈 这个假期努力多更几篇( 理解本算法需对一些< 常 用 >数学概念比较清楚,如复数.虚数.三角函数等(不会的自己查去(其实就是懒得写了(¬︿̫̿¬☆) 整理了一 ...
- [学习笔记] 多项式与快速傅里叶变换(FFT)基础
引入 可能有不少OIer都知道FFT这个神奇的算法, 通过一系列玄学的变化就可以在 $O(nlog(n))$ 的总时间复杂度内计算出两个向量的卷积, 而代码量却非常小. 博主一年半前曾经因COGS的一 ...
- 快速傅里叶变换FFT& 数论变换NTT
相关知识 时间域上的函数f(t)经过傅里叶变换(Fourier Transform)变成频率域上的F(w),也就是用一些不同频率正弦曲线的加 权叠加得到时间域上的信号. \[ F(\omega)=\m ...
随机推荐
- (一)利用 mdb 调试获取 nvlist_t 中 nvpair_t(name/value) 对
服务器:192.168.2.122 root@2236:~# mdb -k> ::spaADDR STATE NAME ...
- WeX5入门之HelloWorld
学习目标:数据双向绑定 在ui2上右键 新建一个应用 然后会出现一个目录 右键hello 在创建页面 选择标准的空白模板 并起一个名 自动生成这两个文件 建立一个input组件 再建一个output组 ...
- TCP确认延时和Nagle算法
TCP确认延时和Nagle算法 nagle 算法是 发送端 收到前一个报文的确认然后再发送下一个tcp数据.这样可以避免大量的小数据. TCP_NODELAY选项控制. Delay ACK是 ...
- pip pytorch安装时出现的问题
pytorch 的安装命令在官网就有,这里就不说了 执行安装命令 pip3 install http://download.pytorch.org/whl/cu80/torch-0.2.0.post3 ...
- discuz过滤词语无效
1.是由于一些特殊的字导致serialize序列化错误.过滤词语在表 common_word中,序列化房子common_syscache的censor中,看看是否有特殊符号.
- 【读书笔记::深入理解linux内核】内存寻址【转】
转自:http://www.cnblogs.com/likeyiyy/p/3837272.html 我对linux高端内存的错误理解都是从这篇文章得来的,这篇文章里讲的 物理地址 = 逻辑地址 – 0 ...
- laravel 中provider的理解和使用
https://segmentfault.com/q/1010000004640866
- python基础--hashlib模块
hashlib模块用于加密操作,代替了md5和sha模块, 主要提供SHA1, SHA224, SHA256, SHA384, SHA512 ,MD5 算法. # -*- coding:utf-8 - ...
- linux定时任务-cron
/sbin/service crond start //启动服务 /sbin/service crond stop //关闭服务 /sbin/service crond restart //重启服务 ...
- IE手工导入证书
打开cer文件->欢迎使用证书导入向导->下一步->将所有的证书放入下列存储->受信任的根证书颁发机构->完成
