EOJ Monthly 2019.2 (based on February Selection) D.进制转换

题目链接：

　　https://acm.ecnu.edu.cn/contest/140/problem/D/

题目：

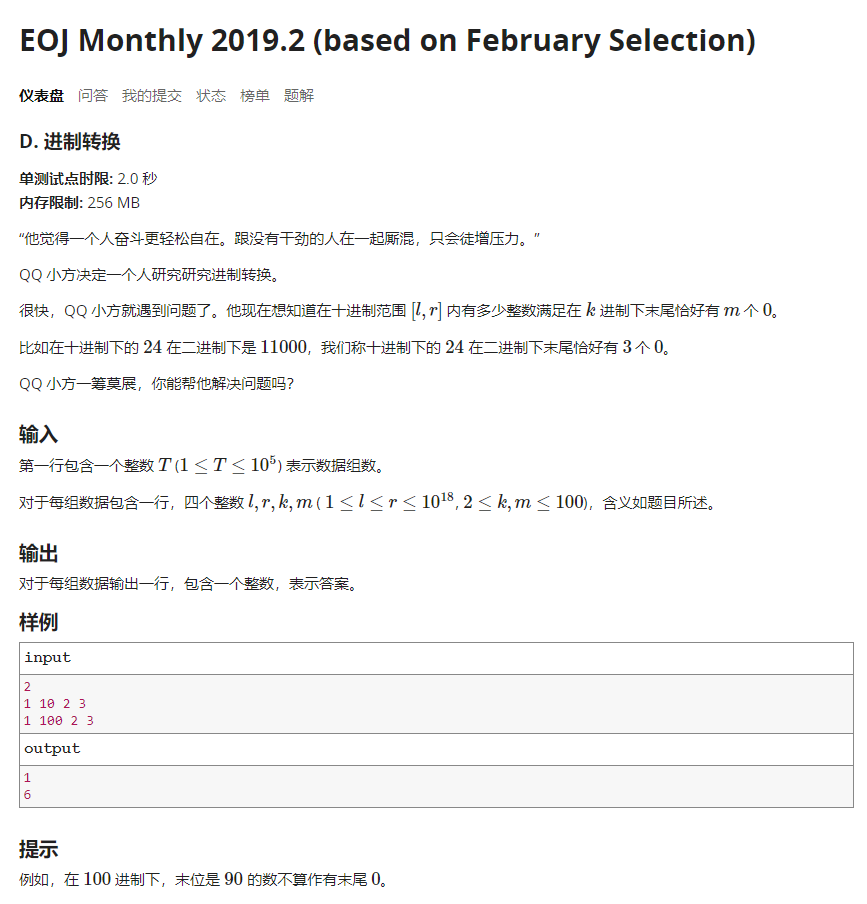
思路：

　　我们知道一个数在某一个进制k下末尾零的个数x就是这个数整除k^x,这题要求刚好末尾有m个0，还需要除去高位为0的情况，因此这题答案就是r / k^x-(l-1)/k^x-(r/k^x+1-(l-1)/k^x+1)。

代码实现如下：

 #include <set>
 #include <map>
 #include <deque>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <ctime>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long LL;
 typedef pair<LL, LL> pLL;
 typedef pair<LL, int> pLi;
 typedef pair<int, LL> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long uLL;

 #define lson rt<<1
 #define rson rt<<1|1
 #define lowbit(x) x&(-x)
 #define name2str(name) (#name)
 #define bug printf("*********\n")
 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
 #define FIN freopen("D://code//in.txt","r",stdin)
 #define IO ios::sync_with_stdio(false),cin.tie(0)

 const double eps = 1e-;
 const int mod = ;
 const int maxn = 2e5 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const LL INF = 0x3f3f3f3f3f3f3f3fLL;

 int t;
 LL l, r, k, m;

 int main(){
     scanf("%d", &t);
     while(t--) {
         scanf("%lld%lld%lld%lld", &l, &r, &k, &m);
         int flag = ;
         LL ans = , tmp = ;
         for(int i = ; i <= m; i++) {
             if(r / tmp < k) {
                 flag = ;
                 break;
             }
             tmp = tmp * k;
         }
         if(!flag) {
             printf("0\n");
             continue;
         }
         ans = r / tmp - (l - ) / tmp;
         if(r / tmp >= k) {
             tmp = tmp * k;
             ans -= r / tmp - (l - ) / tmp;
         }
         printf("%lld\n", ans);
     }
     return ;
 }