BZOJ 3230 相似子串 | 后缀数组 二分 ST表

BZOJ 3230 相似子串

题面

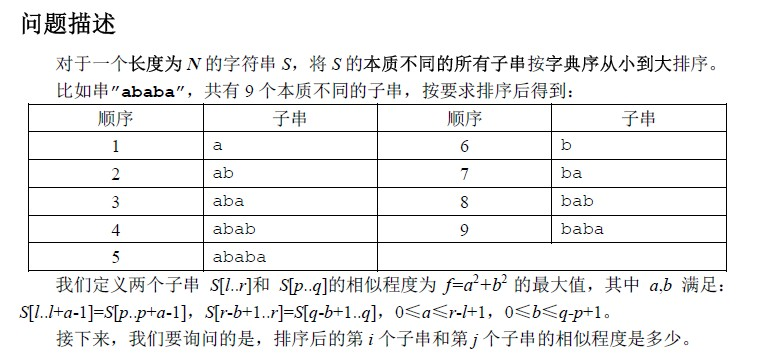
题解

首先我们要知道询问的两个子串的位置。

先正常跑一遍后缀数组并求出height数组。

对于每一个后缀suffix(i)，考虑以i开头的子串有多少是之前没有出现过的，也就是考虑左端点在i、右端点在什么范围内时这个子串没有出现过——答案是右端点在[i + height[i] - 1, n]范围内时这个子串没出现过，即右端点在没有被“i与排在前一个的后缀的公共前缀”覆盖的部分时，这个子串没有出现过。

那么我们记录以每个i开头的新子串的数量，求前缀和，然后询问的时候二分就知道询问的字符串的开头、结尾是谁了。

用已有的height结合st表可以求出两个字符串的最长公共前缀，把字符串倒过来再跑一遍后缀数组，就能求出最长公共后缀了。

注意：

1. 注意两个询问字符串开头/结尾相同的情况。
2. 注意第二个后缀数组是倒过来的。hack数据：2 1 aabc 1 2
3. 注意子串个数爆int，需要开long long。

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){
    char c;
    bool op = 0;
    while(c = getchar(), c > '9' || c < '0')
        if(c == '-') op = 1;
    x = c - '0';
    while(c = getchar(), c >= '0' && c <= '9')
        x = x * 10 + c - '0';
    if(op) x = -x;
}
template <class T>
void write(T x){
    if(x < 0) putchar('-'), x = -x;
    if(x >= 10) write(x / 10);
    putchar('0' + x % 10);
}
const int N = 200005, INF = 0x3f3f3f3f;
char s[N];
int n, Q, buf1[N], buf2[N], sa[2][N], buc[N], rnk[2][N], height[2][N];
ll lg[N], st[2][N][20];
ll sum[N];
void suffix_sort(int t){
    int *x = buf1, *y = buf2, m = 127;
    for(int i = 0; i <= m; i++) buc[i] = 0;
    for(int i = 1; i <= n; i++) buc[x[i] = s[i]]++;
    for(int i = 1; i <= m; i++) buc[i] += buc[i - 1];
    for(int i = n; i; i--) sa[t][buc[x[i]]--] = i;
    for(int k = 1, p = 0; k <= n; k <<= 1, m = p, p = 0){
        for(int i = n - k + 1; i <= n; i++) y[++p] = i;
        for(int i = 1; i <= n; i++) if(sa[t][i] > k) y[++p] = sa[t][i] - k;
        for(int i = 0; i <= m; i++) buc[i] = 0;
        for(int i = 1; i <= n; i++) buc[x[y[i]]]++;
        for(int i = 1; i <= m; i++) buc[i] += buc[i - 1];
        for(int i = n; i; i--) sa[t][buc[x[y[i]]]--] = y[i];
        swap(x, y), x[sa[t][1]] = p = 1;
        for(int i = 2; i <= n; i++)
            if(y[sa[t][i]] == y[sa[t][i - 1]] && y[sa[t][i] + k] == y[sa[t][i - 1] + k]) x[sa[t][i]] = p;
            else x[sa[t][i]] = ++p;
        if(p >= n) break;
    }
    for(int i = 1; i <= n; i++) rnk[t][sa[t][i]] = i;
    for(int i = 1, k = 0; i <= n; i++){
        if(rnk[t][i] == 1) continue;
        if(k) k--;
        int j = sa[t][rnk[t][i] - 1];
        while(i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
        height[t][rnk[t][i]] = k;
    }
}
void init(){
    for(int i = 1, j = 0; i <= n; i++)
        lg[i] = i == (1 << (j + 1)) ? ++j : j;
}
void st_init(int k){
    for(int i = 1; i <= n; i++) st[k][i][0] = height[k][i];
    for(int j = 1; (1 << j) <= n; j++)
        for(int i = 1; i + (1 << j) - 1 <= n; i++)
            st[k][i][j] = min(st[k][i][j - 1], st[k][i + (1 << (j - 1))][j - 1]);
}
ll getmin(int k, int l, int r){
    if(l == r) return INF;
    if(l > r) swap(l, r);
    int j = lg[r - l];
    return min(st[k][l + 1][j], st[k][r - (1 << j) + 1][j]);
}
int main(){
    read(n), read(Q);
    scanf("%s", s + 1);
    init();
    suffix_sort(0);
    st_init(0);
    for(int i = 1, j = n; i < j; i++, j--) swap(s[i], s[j]);
    suffix_sort(1);
    st_init(1);
    for(int i = 1; i <= n; i++) sum[i] = sum[i - 1] + n - sa[0][i] + 1 - height[0][i];
    while(Q--){
        ll a, b, al, bl, ar, br;
        read(a), read(b);
        if(a > sum[n] || b > sum[n]){
            puts("-1");
            continue;
        }
        al = lower_bound(sum + 1, sum + n + 1, a) - sum;
        bl = lower_bound(sum + 1, sum + n + 1, b) - sum;
        ar = rnk[1][n - (sa[0][al] + height[0][al] - 1 + a - sum[al - 1]) + 1];
        br = rnk[1][n - (sa[0][bl] + height[0][bl] - 1 + b - sum[bl - 1]) + 1];
        ll len = min(n - sa[1][ar] + 1 - sa[0][al] + 1, n - sa[1][br] + 1 - sa[0][bl] + 1);
        ll x = min(len, getmin(0, al, bl));
        ll y = min(len, getmin(1, ar, br));
        printf("%lld\n", x * x + y * y);
    }
    return 0;
}