题解-Happy New Year

题解-Happy New Year

Happy New Year

给定 \(n\)，\(m\) 和 \(k\)。有一个序列 \(a\{m\}\) 初始值为 \(0\)。有 \(n\) 种操作，每种可以使 \([L_i,R_i]\) 区间序列值 \(+1\)。每个操作最多用 \(1\) 次（可以不用）。保证对于每个 \(i(1\le i\le n)\) 最多存在 \(k\) 个不同的 \(j\) 满足 \(i\in[L_j,R_j]\)。求最后的序列中奇数最多个数。

数据范围：\(1\le n\le 10^5\)，\(1\le m\le 10^9\)，\(1\le k\le 8\)。

---

状压 \(\texttt{dp}\) 水题，连我这个小蒟蒻都几下就做出来了。

---

从数据范围和时间复杂度入手分析题目：

1. 首先看到 \(n\) 的大小，就知道复杂度中要带个 \(n\)。
2. 时间复杂度中不能带 \(m\)，而且这题也不能二分倍增分治之类的，所以也不带 \(\log m\)。
3. 时间复杂度可以带 \(k\)，甚至还可以带个 \(2^k\)。考虑到这个 \(k\) 真是小到离奇，于是想着带 \(2^k\)——写个状压 \(\texttt{dp}\)。

---

将每个区间 \(i\) 的 \(L_i\) 和 \(R_i+1\) 带信息放进数组 \(p\) 中，按如下的 \(\texttt{cmp}\) 排序：

struct point{
	int op,w,d; //如果是L_i，op=1，w=L_i；如果是R_i，op=-1，w=R_i+1。d=i
	point(int OP=0,int W=0,int D=0){op=OP,w=W,d=D;}
};
int cmp(point x,point y){
	if(x.w==y.w) return x.op<y.op; //※先处理R_i，防止中途当前覆盖区间数 >k
	return x.w<y.w; //按大小排序
}

从左到右枚举每个端点，将当前覆盖着的区间放进数组 \(d\)。

令 \(f_{i,j}\) 表示到第 \(i\) 个端点，选择的区间覆盖状态为 \(j\) 的最大答案。

\(j\) 中二进制下如果第 \(at-1\) 位是 \(1\)，则表示选择了区间 \(d_{at}\) 并且 \(d_{at}\) 正覆盖在当前端点上。

如果 \(at\) 表示该端点在数组 \(d\) 中的位置，那么相邻两个端点之间可以如下递推：

\[\begin{split}
&\textbf{if}\ [p_i. op=1]:\\
&\qquad \textbf{if}\ [at\in j]:f_{i,j}=\max\{f_{i,j},f_{i-1,j}+[|j|\in \mathbb{odd}](p_i. w-p_{i-1}. w)\}\\
&\qquad \textbf{if}\ [at\notin j]:f_{i,j\cup\{at\}}=\max\{f_{i,j\cup\{at\}},f_{i-1,j}+[|j|\in \mathbb{odd}](p_i.w-1-p_{i-1}.w)+[(|j|+1)\in \mathbb{odd}]\}\\
&\textbf{if}\ [p_i. op=-1]:\\
&\qquad \textbf{if}\ [at\notin j]:\\
&\qquad \qquad f_{i,j}=\max\{f_{i,j},f_{i-1,j}+[|j|\in \mathbb{odd}](p_i.w-p_{i-1}.w)\}\\
&\qquad \qquad f_{i,j}=\max\{f_{i,j},f_{i-1,j\cup at}+[(|j|+1)\in \mathbb{odd}](p_i.w-1-p_{i-1}.w)\}+[|j|\in\mathbb{odd}]\}\\
\end{split}
\]

最后的答案就是 \(f_{2n,\varnothing}\)。

---

小蒟蒻怕自己讲不清楚，于是做了个动画：

Input

3 10 2
2 5
5 7
8 9

---

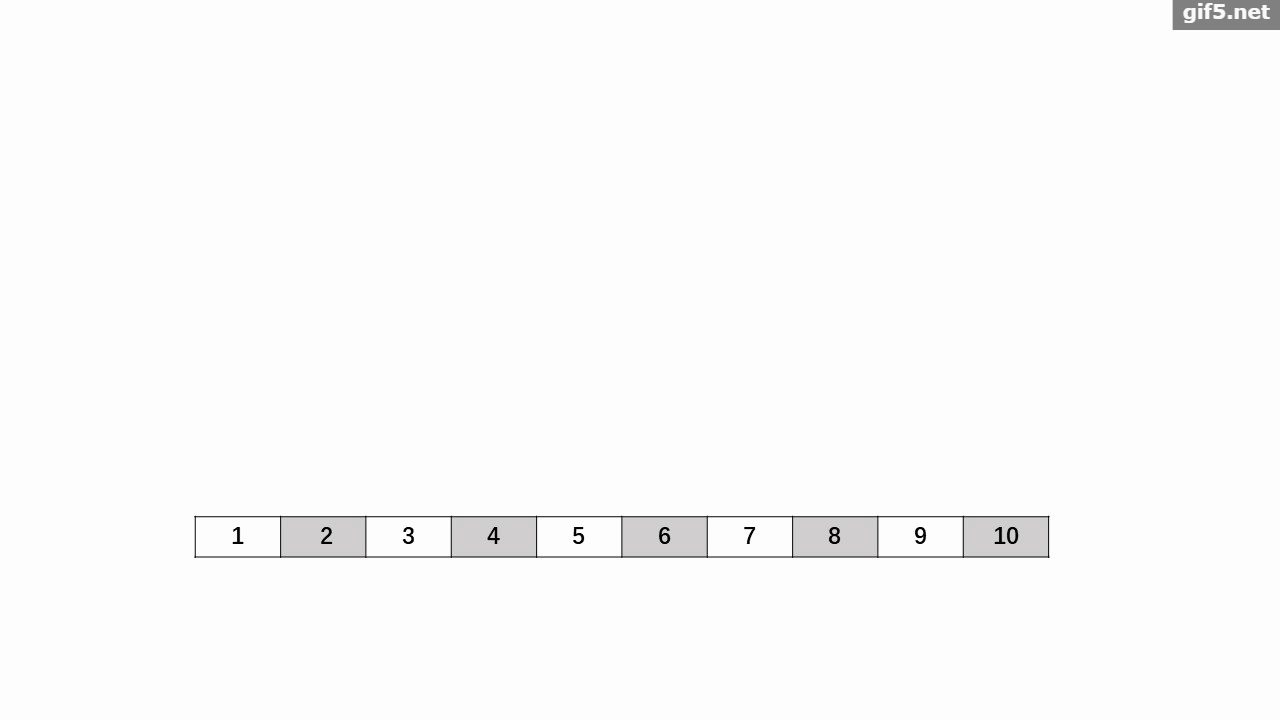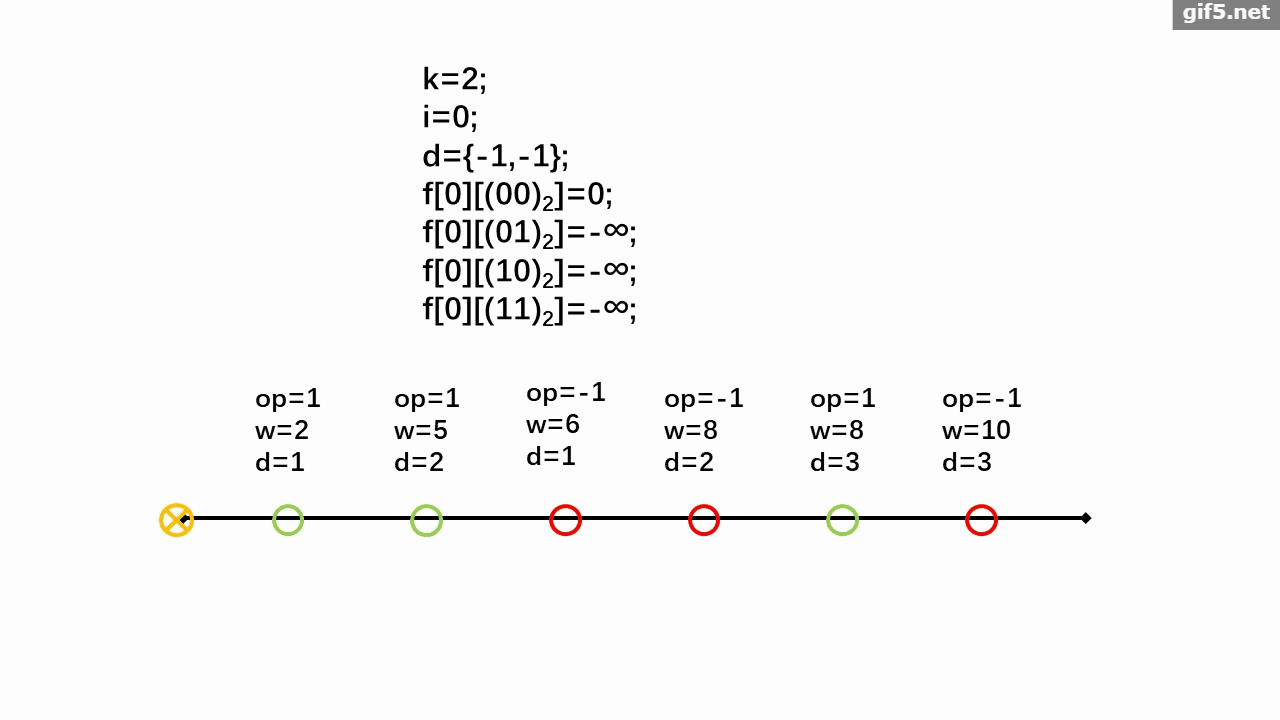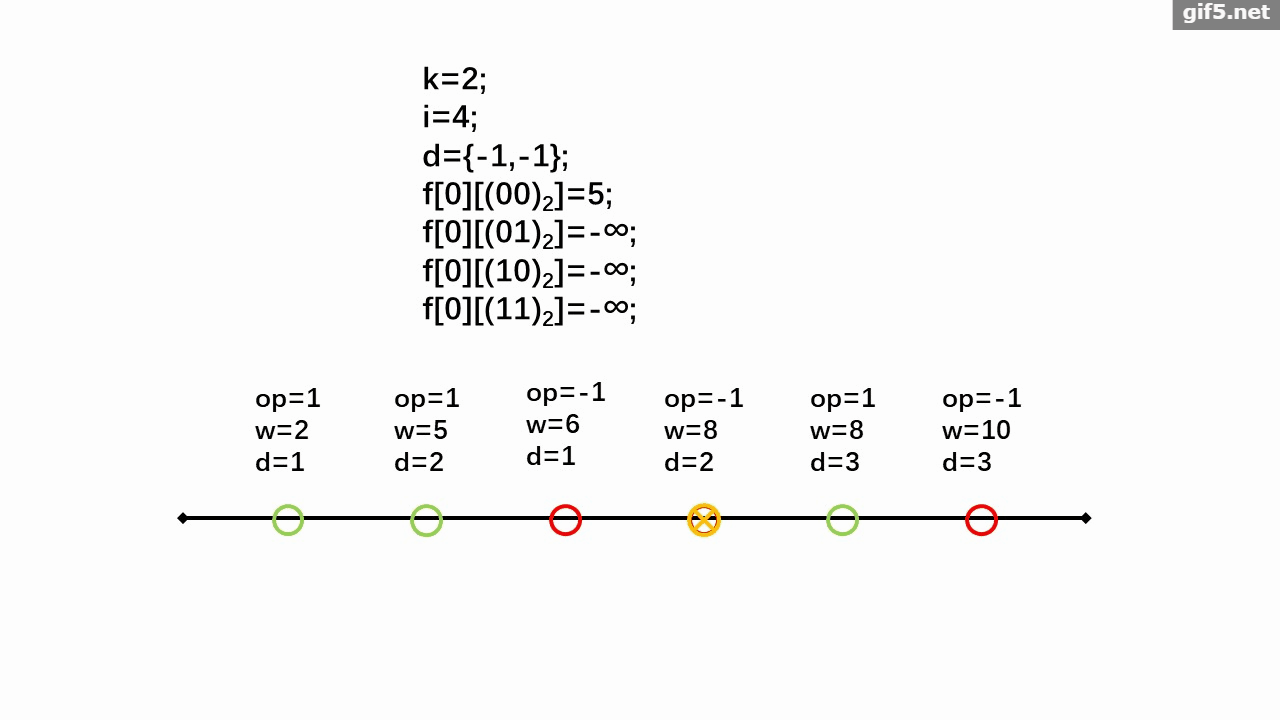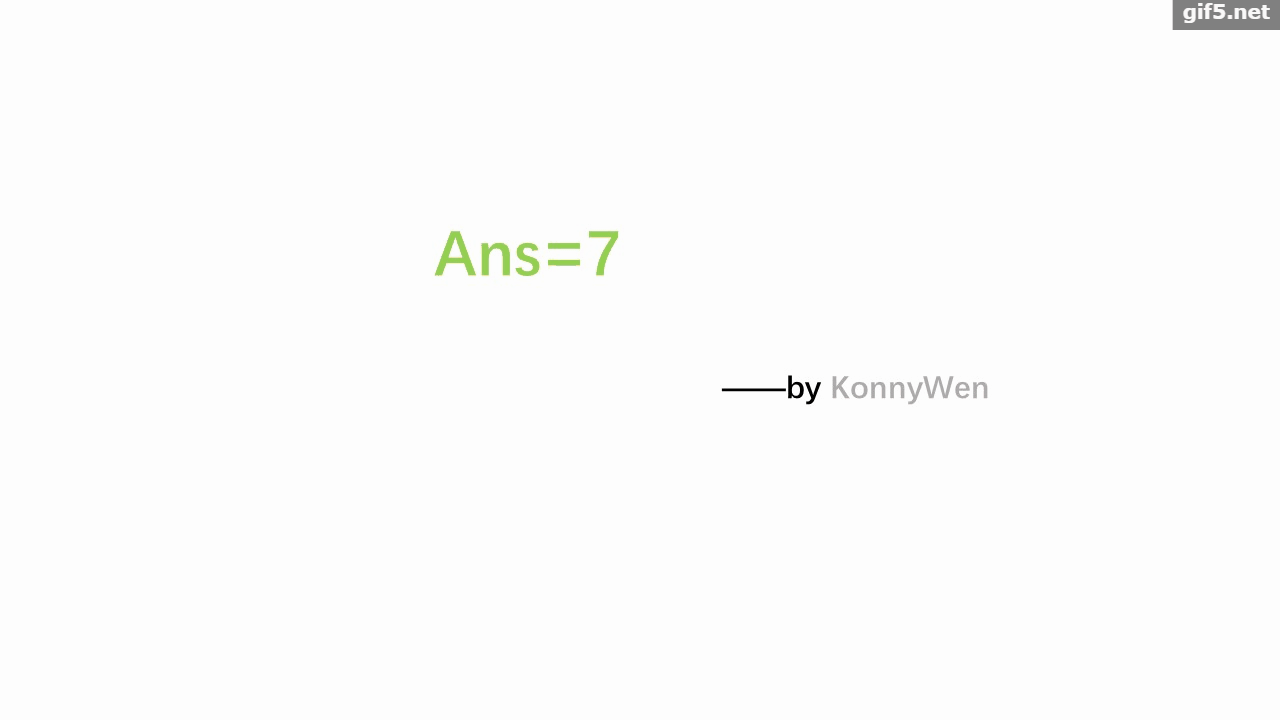
时间复杂度 \(\Theta(n2^k)\)，空间复杂度 \(\Theta(n2^k)\)。

---

Code

蒟蒻的做法比较玄学，但是又很简单，所以放个代码走人吧。

#include <bits/stdc++.h>
using namespace std;

//Start
#define lng long long
#define db double
#define mk make_pair
#define pb push_back
#define fi first
#define se second
#define rz resize
const int inf=0x3f3f3f3f;
const lng INF=0x3f3f3f3f3f3f3f3f;

//Data
const int N=1e5,K=8;
int n,m,k;
int l[N+7],r[N+7];
struct point{
	int op,w,d;
	point(int OP=0,int W=0,int D=0){op=OP,w=W,d=D;}
};
int cmp(point x,point y){
	if(x.w==y.w) return x.op<y.op;
	return x.w<y.w;
}
int pcnt;
point p[(N<<1)+7];

//DP
int d[K+7],one[(1<<K)+7];
int f[(N<<1)+7][(1<<K)+7];
void Max(int&x,int y){x=max(x,y);}
int DP(){
	int ful=(1<<k)-1;
	for(int i=1;i<=ful;i++) one[i]=one[i-(i&-i)]+1;
	for(int i=0;i<=pcnt;i++)
		for(int j=0;j<=ful;j++) f[i][j]=-inf;
	f[0][0]=0;
	for(int j=1;j<=k;j++) d[j]=-1;
	int now=0;
	for(int i=1;i<=pcnt;i++){
		int at=-1;
		if(p[i].op==1){
			for(int j=1;j<=k;j++)
				if(d[j]==-1){at=j,d[j]=p[i].d;break;}
			assert(~at);
			for(int j=0;j<=now;j++)if((j&now)==j){
				Max(f[i][j],f[i-1][j]+(one[j]&1)*(p[i].w-p[i-1].w));
				Max(f[i][j|(1<<(at-1))],f[i-1][j]+(one[j]&1)*(p[i].w-1-p[i-1].w)+((one[j]+1)&1));
			}
			now|=(1<<(at-1));
		} else {
			for(int j=1;j<=k;j++)
				if(d[j]==p[i].d){at=j,d[j]=-1;break;}
			assert(~at);
			now^=(1<<(at-1));
			for(int j=0;j<=now;j++)if((j&now)==j){
				Max(f[i][j],f[i-1][j]+(one[j]&1)*(p[i].w-p[i-1].w));
				Max(f[i][j],f[i-1][j|(1<<(at-1))]+((one[j]+1)&1)*(p[i].w-1-p[i-1].w)+(one[j]&1));
			}
		}
	}
	return f[pcnt][0];
}

//Main
int main(){
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&l[i],&r[i]);
		p[++pcnt]=point(1,l[i],i);
		p[++pcnt]=point(-1,r[i]+1,i);
	}
	sort(p+1,p+pcnt+1,cmp);
	printf("%d\n",DP());
	return 0;
}

---

祝大家学习愉快！