状压DP之LGTB 与序列

题目

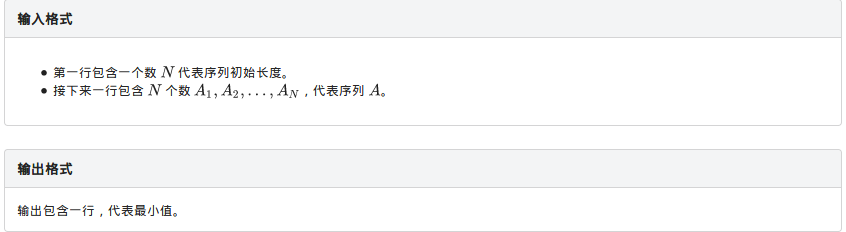
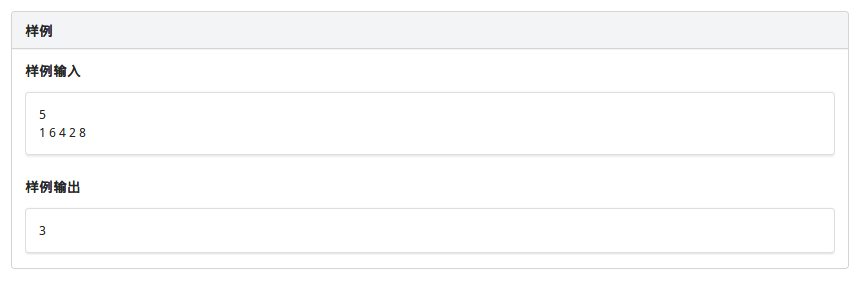
思路

• 这道题竟然是状压DP，本人以为是数论，看都没看就去打下一题的暴力了，哭
  
  \(A_i\)<=30,所以我们只需要考虑1～58个数，再往后选的话还不如选1更优，注意，1是可以重复选取的，因为题目中有一句话
  
  
  
  所以我们所枚举的因子只能包括1～58之间的质因子，而且每个质因子只能选一次，所以选完质因子之后，如果还有剩余的数，就用1填补，而1～58之间的质因子只有16个！！！我们对其进行状压。
• f[i][j]代表处理到第i位j状态下的最优解
• 预处理1～58之间的每一个数的因子，用state数组存放，方便处理，
  
  \(f[0][0]=0\),显然在一个数都不处理的情况下，所得价值为0;
• dp过程和一般状压dp过程差不多，
  
  i枚举处理到的位数（min(16,n)）-->16个质因子都选完不重复，最大为16
  
  S枚举前状态
  
  k枚举要选入的数
  
  判断合法性，!(S&state[k])为合法，显然，如果前一状态已经包含了k的质因子，不合法，
  
  然后进行转移--->

  f[i][S|state[k]]=min(f[i][S|state[k]],f[i-1][S]+abs(k-a[i]));
  

  对当前状态和上一状态加上当前数的贡献取最小值

• 求转移到的状态(min(16,n))的最小值，可能转移完，也可能没有，如果转移完，直接输出就ok了，如果没有，剩下的用1填补，这就涉及到一开始数组排序方式的问题，如果从小到大，最后没有解决的几个值贡献会很大，所以应该从大到小，先解决大块头
  
  附上蒟蒻代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1<<20+1;
int prime[] = {0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};
int f[18][maxn];
int n,a[105];
int state[maxn];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	sort(a+1,a+1+n);
	reverse(a+1,a+1+n);
	for(int i=1;i<=58;i++){
		for(int j=1;j<=16;j++){
			if(i<prime[j])break;
			else if(i%prime[j]==0){
				state[i]|=(1<<(j-1));
			}
		}
	}
	int lim=1<<16;
	int ans=0x7f7f7f7f;
	memset(f,0x3f,sizeof(f));
	f[0][0]=0;
	for(int i=1;i<=min(16,n);i++){
		for(int S=0;S<lim;S++){
			for(int k=1;k<=58;k++){
				if(!(S&state[k])){
					f[i][S|state[k]]=min(f[i][S|state[k]],f[i-1][S]+abs(k-a[i]));
				}
			}
		}
	}
	for(int S=0;S<lim;S++){
		ans=min(ans,f[min(16,n)][S]);
	}
	if(n>16){
		for(int i=17;i<=n;i++)
			ans+=abs(a[i]-1);
	}
	printf("%d\n",ans);
}

推荐状压DP题单(个人觉得比较好的题目，大佬手下留情)

和本题有关：[NOI2015]寿司晚宴

其他：

P1433 吃奶酪

[USACO06NOV]Corn Fields G

[SCOI2005]互不侵犯

[AHOI2009]中国象棋

[SDOI2009]学校食堂

[SDOI2009]Bill的挑战

[NOI2001]炮兵阵地

P2831 愤怒的小鸟

P2915 [USACO08NOV]Mixed Up Cows G

P3052 [USACO12MAR]Cows in a Skyscraper G

P3226 [HNOI2012]集合选数

P4163 [SCOI2007]排列