【DP】斜率优化初步

向y总学习了斜率优化，写下这篇blog加深一下理解。

模板题：https://www.acwing.com/problem/content/303/

分析

因为本篇的重点在于斜率优化，故在此给出状态转移方程：

\(f[i]=\min(f[j]-(t[i]+s)*c[j]+t[i]*c[i]+s*c[n])\) ,其中 \(j \in [1,i-1]\)

其中 \(f[i]\) 表示选取前 \(i\) 个物品后的最小贡献，\(t[i],c[i]\) 分别表示题目中前 \(i\) 个物品 \(t,c\) 的前缀和，\(n,s\) 与题面含义一致。

因为重点在于推式子，所以不理解里面的记号表示什么也不会有太大影响，不过还是尽量先看看朴素的DP怎么写。

如果采取朴素的递推方式解决，那么复杂度是 \(O(N^2)\) ，在 \(N\) 范围较大的时候会超时。

这时候，就要用到主角：斜率优化 了。

首先，因为要让 \(i\) 从 \(1-n\) 一直推过去，所以这里无法优化，因此考虑用更快的方式来找到 \(j\) 。

我们将上面的状态转移方程化为：

\(f[j]=(t[i]+s)*c[j]+f[i]-t[i]*c[i]-s*c[n]\)

注意到枚举 \(i\) 后， \(i\) 就是固定的了，在上面的方程中可以视为一个常数，而 \(j\) 则是变量。

我们将 \(f[j]\) 看作是因变量 \(y\) ， \(c[j]\) 看作是自变量 \(x\) ，上面的式子可以简单地写成：

\[y=k*x+b
\]

其中 \(b=f[i]-t[i]*c[i]-s*c[n]\) ，\(k=(t[i]+s)\) 。

这个形式，正好是直线方程。

我们的目标是最小化 \(f[i]\)，而注意到 \(-t[i]*c[i]-s*c[n]\) 是已经确定的了，所以最小化 \(b\) （直线对应的截距）即可。

因为直线是过点 \(P_{j}(x,y)\) 即 \((c[j],f[j])\) 的，所以下面考虑如何快速找到合适的点，让直线的截距最小化。

将 \(P_{j}(x,y) ~~j \in [1,i-1]\) 画在平面直角坐标系上：

现在要求斜率一定的直线在和什么样的点相交时截距取到最小。

接下来的内容可能需要一点线性规划基础。

1、首先，直线一定和下凸壳上的点相交时截距才可能取到最小：



（上图橙线所连的部分为下凸壳）

简证：假设直线 \(A\) 经过下凸壳上方的点，那么经过下凸壳的点的相同斜率直线 \(B\) 截距更小：

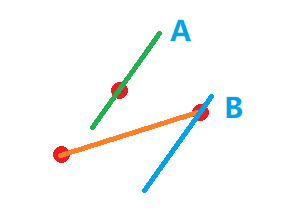
从这一事实中，我们想到维护一个凸包（下凸壳）。

下凸壳具有从左到右斜率递增的性质（所以考虑用单调队列来维护）

2、直线在和从左到右第一条斜率比它大的直线所对应的点（我们记为 \(P\) ）相交时截距最小。

结合图像理解：

证明提示：考虑其他点（分左右讨论），发现没有比这个点更优的了。

下面的工作是实现：（不理解时可以结合代码）

可能需要单调队列基础

先开一个单调队列 q[] ，存点所对应的下标（注意！不是横坐标）

核心是维护一个凸包，注意到在这题中随着 \(i\) 的增加，直线的斜率是递增的，因而在从左到右寻找 \(P\) 的过程中，不是 \(P\) （ \(P\) 左边）的点出队就行了。（出队顺序从左到右）

在找到 \(P\) 后，对应的 \(j\) 就在队头，从而我们可以对 \(f[i]\) 进行更新。

下标 \(i\) 所对应的点是新点，需要进行入队，入队的时候要保证维护下凸壳，因此如果新点和先前的点形成的斜率是小于等于原来的点形成的斜率的，就要将原来的点出队。 （出队顺序从右到左）

如图：

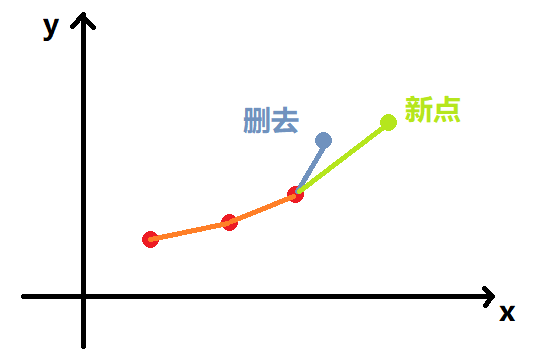
最后将新点入队即可。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N=3e5+5;

int n,s;
ll c[N],t[N];
ll f[N];
int q[N];

int main(){
    cin>>n>>s;
     for(int i=1;i<=n;i++){
        cin>>t[i]>>c[i];
        c[i]+=c[i-1]; t[i]+=t[i-1];
    }

    int tt,hh;
    tt=hh=0; //空的队列是tt=-1, hh=0 而队列一开始是有一个元素的
    q[0]=0;

    for(int i=1;i<=n;i++){
        while(tt>hh && (f[q[hh+1]]-f[q[hh]])<=(t[i]+s)*(c[q[hh+1]]-c[q[hh]]) ) hh++; //弹出左边的点
        int j=q[hh];
        f[i]=f[j]-(t[i]+s)*c[j]+t[i]*c[i]+s*c[n]; //更新f
        while(tt>hh && (__int128)(f[i]-f[q[tt-1]])*(c[q[tt]]-c[q[tt-1]])<=(__int128)(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt-1]])) tt--; //弹出右边的点
        q[++tt]=i;
    }

    cout<<f[n]<<endl;

    return 0;
}

复杂度

注意到每个点只可能入队，出队一次，故复杂度是 \(O(N)\)

扩展

上面例题的情况属于较为简单的情况，所对应的直线斜率随 \(i\) 增加而增加，而且更新点（入队的点）的横坐标也是递增的，因此在寻找 \(P\) 的过程中将 \(P\) 左边的点去掉即可。

但是，在性质不那么好的题目中，是可能出现斜率非单增的情况的，这时候我们就不能在寻找 \(P\) 的过程中将 \(P\) 左边的点去掉，凸包仍然是下凸壳（具有从左到右斜率递增的性质），故可以用二分法来寻找 \(P\) 。

这样做的复杂度是\(O(N\log N)\)

例题：https://www.acwing.com/problem/content/description/304/

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=3e5+5;

ll t[N],c[N];
int n,s;
ll f[N];
int q[N];

int main(){
    cin>>n>>s;
    for(int i=1;i<=n;i++){
        cin>>t[i]>>c[i];
        t[i]+=t[i-1]; c[i]+=c[i-1];
    }

    int tt,hh;
    tt=hh=0;
    q[0]=0;

    for(int i=1;i<=n;i++){
        int l=hh,r=tt;
        while(l<r){
            int mid=l+r>>1;
            if( (t[i]+s)*(c[q[mid+1]]-c[q[mid]])<=f[q[mid+1]]-f[q[mid]] ) r=mid;
            else l=mid+1;
        }

        int j=q[l];
        f[i]=f[j]-(t[i]+s)*c[j]+t[i]*c[i]+s*c[n];
        while(tt>hh && (__int128)(f[i]-f[q[tt-1]])*(c[q[tt]]-c[q[tt-1]])<=(__int128)(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt-1]])) tt--;
        q[++tt]=i;
    }

    cout<<f[n]<<endl;

    return 0;
}

事实上，还有斜率不单调，更新点（入队的点）的横坐标也不单调的情况，这个时候就需要用平衡树等数据结构维护凸包了。