PAT Advanced 1004 Counting Leaves

题目与翻译

1004 Counting Leaves 数树叶 (30分)

A family hierarchy is usually presented by a pedigree tree. Your job is to count those family members who have no child.

一个家族的等级通常是由一个系谱树表示的。你的工作是统计那些没有孩子的家庭成员。

Input Specification:

输入规格:

Each input file contains one test case. Each case starts with a line containing 0<N<100, the number of nodes in a tree, and M (<N), the number of non-leaf nodes. Then M lines follow, each in the format:

每个输入文件包含一个测试用例。每个案例都从一行开始，该行包含0 < n < 100、树中节点的数量和 m (< n)、非叶节点的数量。然后是 m 行，每行格式如下:

ID K ID[1] ID[2] ... ID[K]

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 01.

其中 ID 是表示给定非叶节点的两位数，k 是其子节点的数量，后面是其子节点的两位数 ID 序列。为了简单起见，让我们将根 ID 修改为01。

The input ends with N being 0. That case must NOT be processed.

输入结束时 n 为0。这种情况不能被处理。

Output Specification:

输出规格:

For each test case, you are supposed to count those family members who have no child for every seniority level starting from the root. The numbers must be printed in a line, separated by a space, and there must be no extra space at the end of each line.

对于每一个测试案例，你应该从根本开始计算那些没有子女的家庭成员的资历水平。数字必须打印在一行中，由一个空格分隔，并且在每行的末尾必须没有额外的空格。

The sample case represents a tree with only 2 nodes, where 01 is the root and 02 is its only child. Hence on the root 01 level, there is 0 leaf node; and on the next level, there is 1 leaf node. Then we should output 0 1 in a line.

示例案例表示一个只有2个节点的树，其中01是根，02是它的唯一子节点。因此，在根01级上，有0个叶节点; 在下一级上，有1个叶节点。那么我们应该在一行中输出01。

Sample Input:

样本输入:

2 1
01 1 02

Sample Output:

示例输出:

0 1

理解与算法

简单地讲，这道题就是在求一棵多叉树的叶子节点的数量，并按照层的顺序打印！如果没有叶子结点就打印0，否则输出叶子结点个数。

粗略地想一想，层序遍历和前序遍历都可以完成，这里用的是深度优先算法，也就是先序遍历。

给出一个样例的示意图：

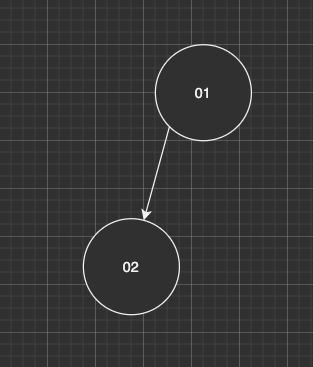
01是根节点，因为它有一个子节点02所以它不是叶子结点，而02是叶子结点，因此最后的输出为：

0 1

接下来来实现程序。

处理输入

// 全局变量
vector<int> nodes[100]; // 每个元素代表一个节点链表
int pedigree[100];  // 族谱树中每一层的叶子结点的数量
int pedigree_depth = -1; // 族谱树的最大深度

int main...(省略部分)
int N, M, node, num, child;
// 处理第一行
cin >> N >> M;
// 遍历所有的非叶节点，构建节点链表
for (int i = 0; i < M; ++i) {
    cin >> node >> num;
    for (int j = 0; j < num; ++j) {
        cin >> child;
        nodes[node].push_back(child);
    }
}

这里用了一个vector的数组来存储每个节点的子节点链表。

遍历族谱树

/**
 * 深度优先算法，遍历整个家族树，如果找到叶子结点就加入到全局变量数组中
 * @param index 下标
 * @param depth 深度
 */
void dfs(int index, int depth) {
    if (nodes[index].empty()) {
        // 如果这个节点没有子节点，那么就是叶子结点
        pedigree[depth]++;
        // 这个叶子结点的深度如果超过原本记录的最大深度，那么就更新最大深度
        pedigree_depth = depth > pedigree_depth ? depth : pedigree_depth;
        return;
    }
    // 遍历该节点的所有子节点
    for (int i : nodes[index]) {
        // 因为往下走了一层，所以深度加1
        dfs(i, depth + 1);
    }
}

为了提高效率，不用每次都遍历整个族谱叶子个数的数组，我们可以使用一个全局变量pedigree_length来确定整个数组的长度，提高最后的打印效率。

输出

// 数组默认值为0，这里输出这个数组的全部内容，长度为pedigree_length
cout << pedigree[0];
for (int i = 1; i <= pedigree_depth; ++i) {
    cout << " " << pedigree[i];
}

代码实现

#include <iostream>
#include <vector>

using namespace std;

vector<int> nodes[100]; // 每个元素代表一个节点链表
int pedigree[100];  // 族谱树中每一层的叶子结点的数量
int pedigree_depth = -1; // 族谱树的最大深度

/**
 * 深度优先算法，遍历整个家族树，如果找到叶子结点就加入到全局变量数组中
 * @param index 下标
 * @param depth 深度
 */
void dfs(int index, int depth) {
    if (nodes[index].empty()) {
        // 如果这个节点没有子节点，那么就是叶子结点
        pedigree[depth]++;
        // 这个叶子结点的深度如果超过原本记录的最大深度，那么就更新最大深度
        pedigree_depth = depth > pedigree_depth ? depth : pedigree_depth;
        return;
    }
    // 遍历该节点的所有子节点
    for (int i : nodes[index]) {
        // 因为往下走了一层，所以深度加1
        dfs(i, depth + 1);
    }
}

int main() {
    int N, M, node, num, child;
    // 处理第一行
    cin >> N >> M;
    // 遍历所有的非叶节点，构建节点链表
    for (int i = 0; i < M; ++i) {
        cin >> node >> num;
        for (int j = 0; j < num; ++j) {
            cin >> child;
            nodes[node].push_back(child);
        }
    }
    // 对族谱树进行深度优先遍历
    dfs(1, 0);
    // 数组默认值为0，这里输出这个数组的全部内容，长度为pedigree_length
    cout << pedigree[0];
    for (int i = 1; i <= pedigree_depth; ++i) {
        cout << " " << pedigree[i];
    }
    return 0;
}