Codeforces Round #628 (Div. 2) 题解

人闲桂花落，夜静春山空。

月出惊山鸟，时鸣春涧中。——王维

A. EhAb AnD gCd

You are given a positive integer x. Find any such 2 positive integers a and b such that GCD(a,b)+LCM(a,b)=x.

As a reminder, GCD(a,b) is the greatest integer that divides both a and b. Similarly, LCM(a,b) is the smallest integer such that both a and b divide it.

It's guaranteed that the solution always exists. If there are several such pairs (a,b), you can output any of them.

Input

The first line contains a single integer t (1≤t≤100) — the number of testcases.

Each testcase consists of one line containing a single integer, x

(2≤x≤10^9).

Output

For each testcase, output a pair of positive integers a and b (1≤a,b≤109) such that GCD(a,b)+LCM(a,b)=x. It's guaranteed that the solution always exists.

If there are several such pairs (a,b), you can output any of them.

Example

input

2
2
14

output

1 1
6 4

Note

In the first testcase of the sample, GCD(1,1)+LCM(1,1)=1+1=2.

In the second testcase of the sample, GCD(6,4)+LCM(6,4)=2+12=14.

题目大意：给定正整数x，找到两个正整数a、b，使得GCD(a，b) + LCM(a，b) = x。

显然，这道题只需要求一可行解即可，并非需要数论进行思考。

考虑：1，x - 1，满足题意。

代码：

#include<iostream>
#include<cstdio>

using namespace std;
int main()
{
	int T;
	scanf("%d", &T);
	while(T --)
	{
		int x;
		scanf("%d", &x);
		printf("1 %d\n", x - 1);
	}
	return 0;
}

B. CopyCopyCopyCopyCopy

Ehab has an array a of length n. He has just enough free time to make a new array consisting of n copies of the old array, written back-to-back. What will be the length of the new array's longest increasing subsequence?

A sequence a is a subsequence of an array b if a can be obtained from b by deletion of several (possibly, zero or all) elements.The longest increasing subsequence of an array is the longest subsequence such that its elements are ordered in strictly increasing order.

Input

The first line contains an integer t — the number of test cases you need to solve. The description of the test cases follows.

The first line of each test case contains an integer n (1≤n≤105) — the number of elements in the array a.

The second line contains n space-separated integers a1, a2, …, an

(1≤ai≤109)

— the elements of the array a.

The sum of n across the test cases doesn't exceed 105.

Output

For each testcase, output the length of the longest increasing subsequence of a if you concatenate it to itself n times.

Example

input

2
3
3 2 1
6
3 1 4 1 5 9

output

3
5

Note

In the first sample, the new array is [3,2,1,3,2,1,3,2,1]. The longest increasing subsequence is marked in bold.

In the second sample, the longest increasing subsequence will be [1,3,4,5,9].

保证严格单调递增的选取方法:排序、去重。

代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>

using namespace std;
const int maxn = 300000 + 5;
int n, a[maxn];
int main()
{
	int T, cnt = 0;
	scanf("%d", &T);
	while(T --)
	{
		scanf("%d", &n);
		for(int i = 0; i < n; ++ i)
			scanf("%d", &a[i]);

		sort(a, a + n);
		for(int i = 0; i < n; ++ i)
			if(!i || a[i] != a[i - 1]) ++ cnt;
		printf("%d\n", cnt);
		memset(a, 0,  sizeof(a));
		cnt = 0;
	}
	return 0;
}

C. Ehab and Path-etic MEXs

You are given a tree consisting of n nodes. You want to write some labels on the tree's edges such that the following conditions hold:

Every label is an integer between 0 and n−2 inclusive.

All the written labels are distinct.

The largest value among MEX(u,v) over all pairs of nodes (u,v) is as small as possible.

Here, MEX(u,v) denotes the smallest non-negative integer that isn't written on any edge on the unique simple path from node u to node v.

Input

The first line contains the integer n

(2≤n≤10^5)

— the number of nodes in the tree.

Each of the next n−1 lines contains two space-separated integers u and v (1≤u,v≤n) that mean there's an edge between nodes u and v. It's guaranteed that the given graph is a tree.

Output

Output n−1 integers. The ith of them will be the number written on the ith edge (in the input order).

Examples

input

3
1 2
1 3

output

0
1

input

6
1 2
1 3
2 4
2 5
5 6

output

0
3
2
4
1

Note

The tree from the second sample:

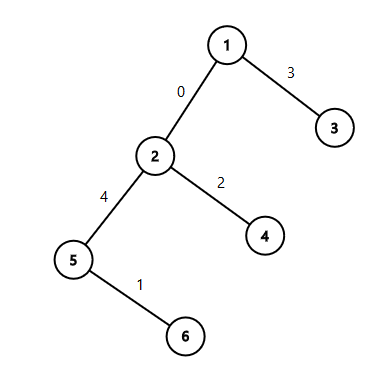
我当时思路是这样子：如果一条边出现在所有路径中的次数多于另一条边，那么它的边权成为为价值的最大值就更不容易。

因为它出现次数最多，意味着多数情况下路径的价值不用考虑它。

因此，我们就对这棵树每条边计算它的出现次数，排序；次数多的分支越应该优先填大的数。

代码：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cstdio>
#include<cmath>
#define pil pair <int, long long>
#define maxn 3000000 + 5

using namespace std;
vector <int> G[maxn];
pil table[maxn];

int n, size[maxn] = {}, ans[maxn] = {}, fa[maxn] = {};
int input[maxn][2];
bool cmp(pil x, pil y)
{
	return x.second < y.second;
}
void dfs(int Fa, int x)
{
	fa[x] = Fa;
	for(int i = 0; i < G[x].size(); ++ i)
	{
		int v = G[x][i];
		if(v != Fa)
		{
			dfs(x, v);
			size[x] += size[v];
		}
	}
	++ size[x];
	return;
}
int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; ++ i) G[i].clear();

	for(int i = 1; i < n; ++ i)
	{
		scanf("%d %d", &input[i][0], &input[i][1]);
		G[input[i][1]].push_back(input[i][0]);
		G[input[i][0]].push_back(input[i][1]);
	}
	dfs(0, 1);
	for(int i = 1; i < n; ++ i)
	{
		int x = input[i][0], y = input[i][1];
		table[i].first = i;
		if(fa[x] == y) table[i].second = (long long) size[x] * (n - size[x]);
		else
		{
			table[i].second = (long long) size[y] * (n - size[y]);
		}
	}
	sort(table + 1, table + n, cmp);
	for(int i = 1; i < n; ++ i) ans[table[i].first] = i;
	for(int i = 1; i < n; ++ i)
		printf("%d\n", ans[i] - 1);

	return 0;
}

D. Ehab the Xorcist

Given 2 integers u and v, find the shortest array such that bitwise-xor of its elements is u, and the sum of its elements is v.

Input

The only line contains 2 integers u and v (0≤u,v≤1018).

Output

If there's no array that satisfies the condition, print "-1". Otherwise:

The first line should contain one integer, n, representing the length of the desired array. The next line should contain n positive integers, the array itself. If there are multiple possible answers, print any.

Examples

input

2 4

output

2
3 1

input

1 3

output

3
1 1 1

input

8 5

output

-1

input

0 0

output

0

Note

In the first sample, 3⊕1=2 and 3+1=4. There is no valid array of smaller length.

Notice that in the fourth sample the array is empty.

这道题我第一反应使用搜索。

...

迭代加深搜索啊！！

...

怎么剪枝？？

...

其实，如果加上剪枝，效率依旧不如以下做法：

考虑d = v - u，若d < 0 或者 d是奇数，输出-1。

为什么？因为数的累和>=异或和，而第一位数相加与异或的结果应该是一样的，因此u和v奇偶性相同。

再考虑：让第一个数是u，再让后两个数与第一个数凑出v，后两个数异或和为0；

不难想到：a = u，b = d / 2，c = d / 2；

由于d一定为偶数，刚刚讲过了，满足题意。

那么是否存在两个解呢？

a = u + d / 2，b = d / 2，如果a和b异或值等于v，即满足题意。

如果d = 0，那么仅需要a即可。

如果u = v = 0，则不需要啦。

代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>

using namespace std;
long long u, v, d;
int main()
{
	scanf("%lld %lld", &u, &v);
	d = v - u;
	if(d < 0 || d & 1) puts("-1");
	else
	{
		if(d == 0)
		{
			if(u == 0)
			{
				puts("0");
			}
			else
			{
				puts("1");
				printf("%lld\n", v);
			}
			return 0;
		}
		if(((u + (d >> 1)) ^ (d >> 1)) == u)
		{
			puts("2");
			printf("%lld %lld\n", u + (d >> 1), d >> 1);
			return 0;
		}
		puts("3");
		printf("%lld %lld %lld\n", u, d >> 1, d >> 1);
	}
	return 0;
}