PCoA|NMDS|STRESS|RDA |RA|Unimodal|CCA|Generalized Joint Attribute Modeling

PCoA：主坐标轴分析

数值型变量使用各种距离公式，而分类变量看是否相同，比如，

Aabbcc

||

Aaffff

其中，两个相同，4个不同，一组6个,则（6+6-2*2）=8。

PC0A与PCA区别在于PCoA有多种计算距离公式。

NMDS：

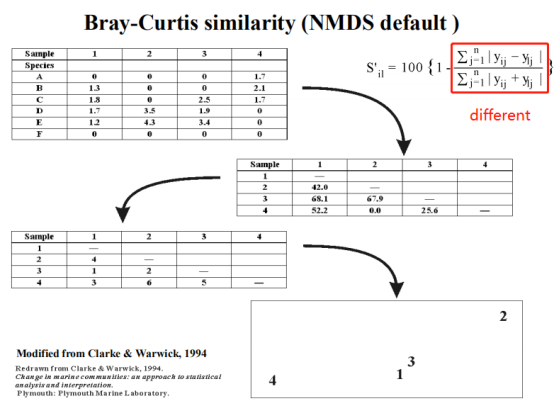
两者之差比两者之和，得到similarity得分，按分排序。所以，S是similarity，值越大越相似。

对差距不敏感只有排序，多一个物种或者类群差距都不大，稳健性。

STRESS来衡量转换的好坏，低于0.05比较好。

RDA or RA用矩阵解释矩阵，以前是用矩阵解释向量。Eg：用生化指标（10项）解释身高、体重和血压。

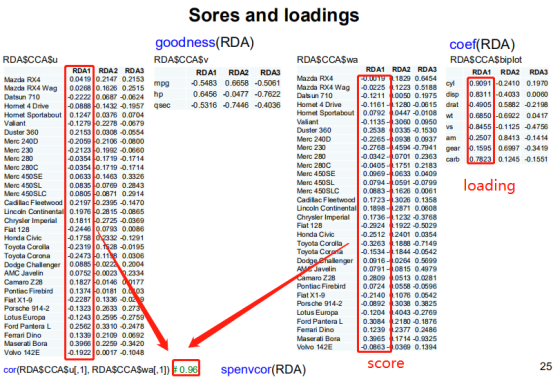
原理是将矩阵转化为向量，最后用向量解释向量，即得到两个RDA1之间的相关系数。

Loading 是每一列的变量，就是每个主成分含有多少轴，score是每一个sample对应的值。即一个主成分中可能有N个轴，就是一个主成分占有N个变量。

用RDA不能解释的部分用PCA解释：

Triplot：y变量，x变量，score值

分成两大类之后，分析各类对变量的影响：

散点图判断两两之间的单调性，如果是单调则使用RDA，非单调使用CCA。

CCA使用卡方分布，其余与RDA相同。

Unimodal是单峰非线性的，如果是双峰或者更复杂关系则不能使用。

Generalized Joint Attribute Modeling：

James S. Clark is Nicholas Professor of the Nicholas School of the Environment and Professor of Statistical Science. Clark’s research focuses on how global change affects populations, communities, and ecosystems.