【一致性检验指标】Kappa(cappa)系数

1 定义

百度百科的定义：

它是通过把所有地表真实分类中的像元总数（N）乘以混淆矩阵对角线（Xkk）的和，再减去某一类地表真实像元总数与被误分成该类像元总数之积对所有类别求和的结果，再除以总像元数的平方减去某一类中地表真实像元总数与该类中被误分成该类像元总数之积对所有类别求和的结果所得到的。

这对于新手而言可能比较难理解。什么混淆矩阵？什么像元总数？

我们直接从算式入手：

\[k = \frac{p_0-p_e}{1-p_e}
\]

\(p_0\)是每一类正确分类的样本数量之和除以总样本数，也就是总体分类精度

假设每一类的真实样本个数分别为\(a_1,a_2,...,a_c\)

而预测出来的每一类的样本个数分别为\(b_1,b_2,...,b_c\)

总样本个数为n

则有：\(p_e=a_1×b_1+a_2×b_2+...+a_c×b_c / n×n\)

1.1 简单例子

学生考试的作文成绩，由两个老师给出 好、中、差三档的打分，现在已知两位老师的打分结果，需要计算两位老师打分之间的相关性kappa系数：



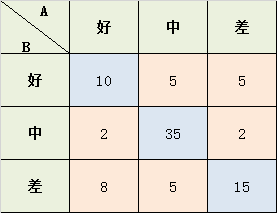
从上面的公式中，可以知道我们其实只需要计算\(p_0 ,p_e\)即可：

Po = (10+35+15) / 87 = 0.689

a1 = 10+2+8 = 20; a2 = 5+35+5 = 45; a3 = 5+2+15 = 22;

b1 = 10+5+5 = 20; b2 = 2+35+2 = 39; b3 = 8+5+15 = 28;

Pe = (a1b1 + a2b2 + a3b3) / (8787) = 0.455

K = (Po-Pe) / (1-Pe) = 0.4293578

可以说提到kappa到处都是两个老师的例子，哈哈

2 指标解释

kappa计算结果为[-1,1]，但通常kappa是落在 [0,1] 间

第一种分析准则--可分为五组来表示不同级别的一致性：

0.0~0.20极低的一致性(slight)

0.21~0.40一般的一致性(fair)

0.41~0.60 中等的一致性(moderate)

0.61~0.80 高度的一致性(substantial)

0.81~1几乎完全一致(almost perfect)