LeetCode二分专题

二分

二分模板

两个模板：1.最大值最小模板一，2.最小值最大用模板二

单调性、两段性的性质

版本1：二分绿色端点是答案，最大值最小

int bsearch_1(int l, int r){
    while (l < r){
        int mid = l + r >> 1; //下取整
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

版本2：二分红色端点是答案，最小值最大

int bsearch_2(int l, int r){
    while (l < r){
        int mid = l + r + 1 >> 1; //上取整
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

模板2要+1后再下取整

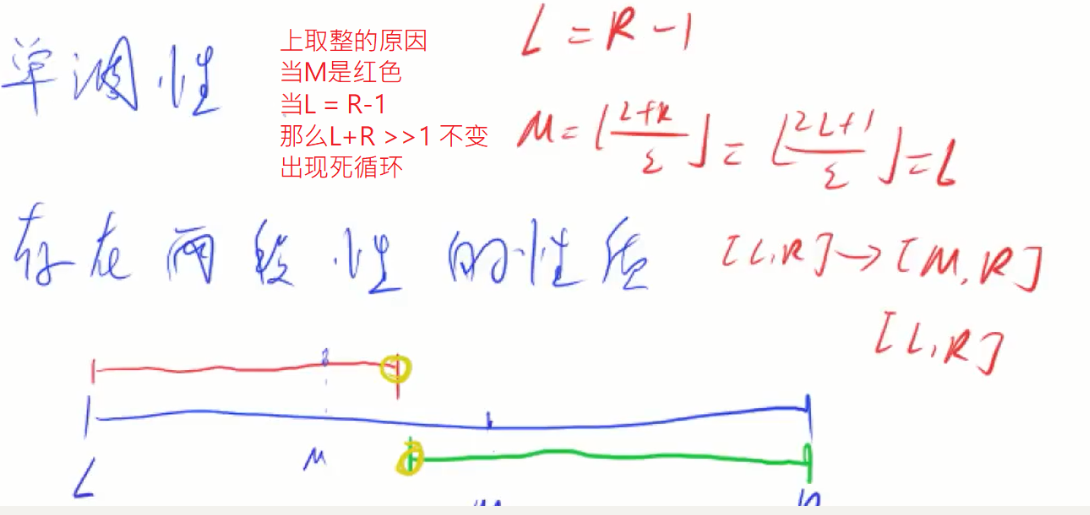
二分最后l和r相等

模板小结：

69. x 的平方根

check性质：t的平方<=x

找最小值最大，模板2

注意精度：long long mid = (long long )(l + (long long ) r + 1) >> 1;

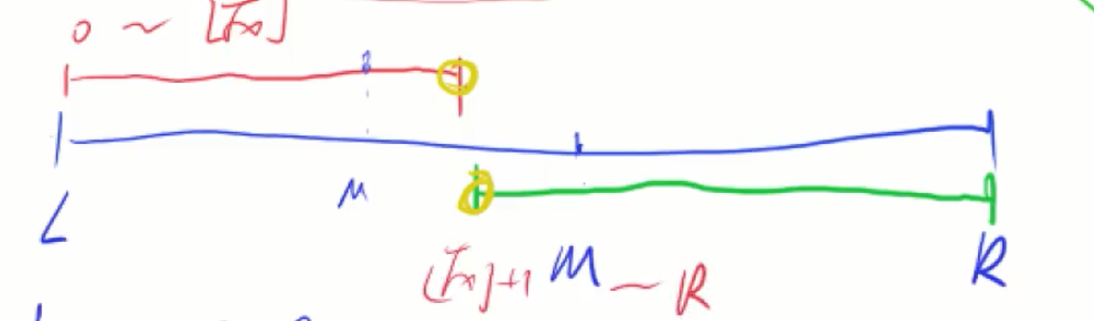
class Solution {
public:

    bool check(long long  mid,int x){
        return mid*mid <= x;
    }

    int mySqrt(int x) {
        int l = 0,r = x;
        while (l < r){
            long long  mid = (long long )(l + (long long ) r + 1) >> 1;
            if(check(mid,x)) l = mid;
            else r = mid - 1;
        }
        return l;
    }
};

35. 搜索插入位置

check性质：t>=x，即第一个比x大或等的位置

最大值最小，模板1

class Solution {
public:
    bool check(int mid,int x){
        return mid >= x;
    }
    int searchInsert(vector<int>& nums, int target) {
        if(nums.size() == 0 || nums.back() < target) return nums.size();
        int l = 0,r = nums.size()-1;
        while(l<r){
            long long mid = (long long )(l + r )>>1;
            if(check(nums[mid],target)) r = mid;
            else l = mid + 1;
        }
        return l;
    }
};

34. 在排序数组中查找元素的第一个和最后一个位置

两个性质

1.check1：t>=x，找大于等于8的第一个位置，最大值最小，模板1

2.check2：t<=x，找小于等于8的最后1个位置，最小值最大，模板2

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.size() == 0) return {-1,-1};
        int l = 0,r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        if(nums[l] != target) return {-1,-1};
        int start = l;
        l = 0,r = nums.size() - 1;
        while(l < r){
            int mid = l + r + 1  >> 1;
            if(nums[mid] <= target) l = mid;
            else r = mid - 1;
        }
        return {start, l};
    }
};

74. 搜索二维矩阵

最大值最小

或者最小值最大，找到目标即可

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if(matrix.size() == 0 || matrix[0].size() == 0) return false;
        int n = matrix.size();
        int m = matrix[0].size();
        int l = 0 ,r = n * m - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(matrix[mid/m][mid%m] >= target) r = mid;
            else l = mid + 1;
        }
        if(matrix[r/m][r%m] == target) return true;
        return false;
    }
};

153. 寻找旋转排序数组中的最小值

check性质，nums[mid] <= nums.back() ，且找最大(右半段)满足的最小下标

或者 nums[mid] < nums[0]，且找最小值最大

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.size() == 0) return 0;
        int l = 0,r = nums.size()-1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] <= nums.back()) r = mid;
            else l = mid + 1;
        }
        return nums[r];
    }
};

33. 搜索旋转排序数组

思路，按153思路，先找最小值，分成两段；然后按74题思路(最大值最小,且>=target)

两次二分，注意r--后的边界

class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.size() == 0) return -1;
        int l = 0,r = nums.size()-1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] <= nums.back()) r = mid;
            else l = mid + 1;
        }
        if(target <= nums.back()) r = nums.size()-1;
        else l = 0,r--;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        if(target == nums[l]) return l; //这里要用l 否则之前r-- r可能是-1
        return -1;
    }
};

278. 第一个错误的版本

这道题给了check函数，两段，第一个出错的版本只需要找最大值最小

注意溢出 long long mid = (long long )(l + r >> 1);

// The API isBadVersion is defined for you.
// bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        long long  l = 1 ,r = n;
        while(l < r){
            long long mid = (long long )(l + r >> 1);
            if(isBadVersion(mid) == true) r = mid;
            else l = mid + 1;
        }
        return r;
    }
};

162. 寻找峰值

难度中等190 返回任何一个峰值所在位置即可。

方法1：线性扫描一遍

方法2：二分，比较mid 和 mid+1 如果mid+1的值比mid值大与等于那么mid+1后肯定有峰值，如果mid比mid+1小说明左边或者mid一定存在峰值

边界不需要判，分析：while循环里mid不会等于最后1个点，因为当mid=最后1个点，说明l=r都等于最后1个点，那么就退出循环了

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int l = 0 , r = nums.size()-1;
        while( l < r){
            int mid = l + r >> 1;
            if(nums[mid] < nums[mid+1]) l = mid + 1;
            else r = mid;
        }
        return l;
    }
};

287. 寻找重复数

只能使用额外的 O(1) 的空间。

时间复杂度小于 O(n^2) 。

二分答案，二分这个数值，O(N)遍历一遍数组统计在L_{mid区间内的数的个数，如果个数比区间大小大那么说明有一个重复，重复的数就在这个L}mid闭区间中，让r=mid，否则在左区间(不包含mid)让L=mid+1

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n = nums.size() - 1;
        int l = 1, r = n;
        while( l < r){ //二分答案 二分这个数是多少
            int mid = l + r >> 1;
            int cnt = 0;
            for(int i=0;i < nums.size();i++){
                if(nums[i] >= l && nums[i] <= mid) cnt++;
            }
            if(cnt > mid - l + 1) r = mid;
            else l = mid + 1;
        }
        return r;
    }
};

275. H指数 II

满足单调性，二分

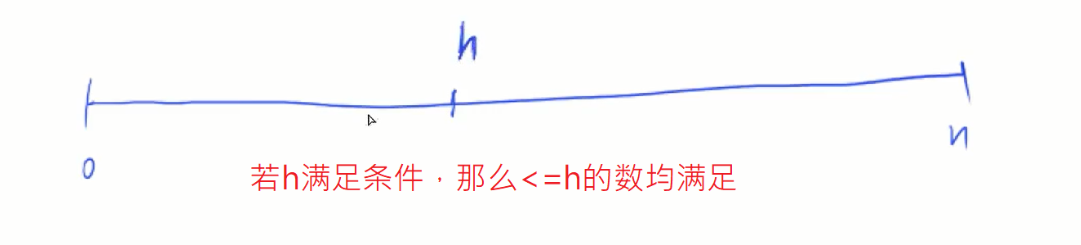
最小值最大；l最小为0，r最大为n = size个

h满足，h-1也一定满足，可以把区间分成两部分，前一部分红色一定满足，绿色不满足，所以就是找最小值最大

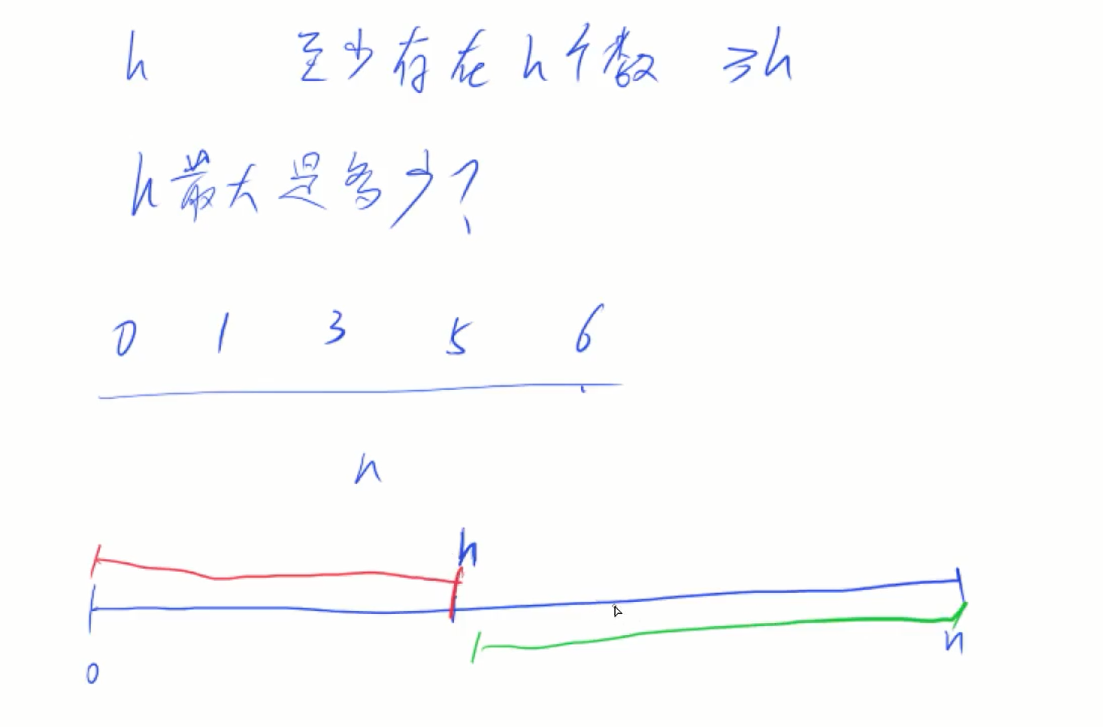
class Solution {
public:
    int hIndex(vector<int>& citations) {
        int n = citations.size() - 1;
        int l = 0, r = citations.size();
        while(l < r){
            int mid = (l + r + 1) >> 1;
            if(citations[n - mid + 1] >= mid) l = mid;
            else r = mid - 1;
        }
        return l;
    }
};