设计模式之GOF23享元模式

享元模式FlyWeight

场景：如果有很多个完全相同或者相似的对象，可以节省内存资源

核心：

享元模式以共享的方式高效地支持大量细粒对象的重用

享元对象做到共享的关键是区分了内部状态和外部状态：

内部状态：可以共享，不会随环境变化而变化（共有的部分）

外部状态：不可以共享，会随环境变化而改变（独特的部分）

享元模式的实现：

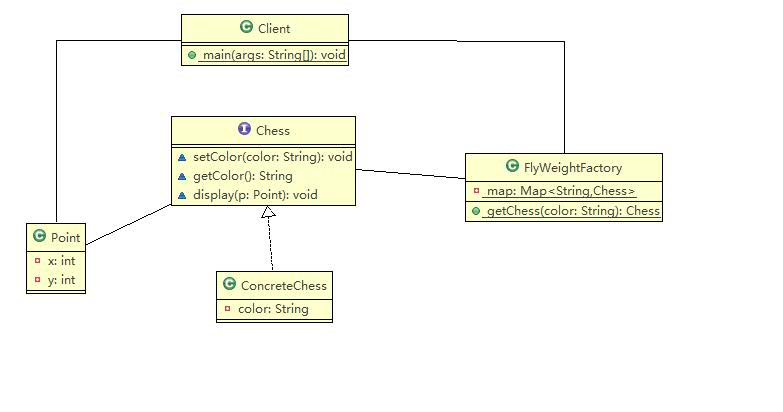
-FlyweightFactory享元工厂类：创建并管理享元对象，享元池一般设计成键值对

-FlyWeight抽象享元类 ：通常是一个接口或抽象类 声明公共方法，这些方法可以向外界提供对象的内部状态 设置外部状态

-ConcreteFlyWeight具体享元类：为内部状态提供成员变量进行储存

-UnsharedConcreteFlyWeught非共享享元类：不能被共享的子类可以设计成非共享享元类

在实际中的场景：线程池，数据库连接池，String类

优点：极大减少内存中对象的数量；相同或者相似的对象只存一份，节约资源；外部状态相对独立，不影响内部状态

缺点：模式复杂，程序逻辑复杂化；为了节省内存，共享了内部状态，分理出外部状态，读取外部状态使运行时间变长，时间换取空间

例如：围棋（内部状态：颜色形状大小  外部状态：位置）

/**
 * 外部状态类UnsharedConcreteFlyWeight
 * @author 小帆敲代码
 *
 */
public class Point {
 private int x;
 private int y;
 
public Point(int x, int y) {
 this.x = x;
 this.y = y;
}

public int getX() {
 return x;
}

public void setX(int x) {
 this.x = x;
}

public int getY() {
 return y;
}

public void setY(int y) {
 this.y = y;
}

}

/**
 * 享元类
 * @author 小帆敲代码
 *
 */
public interface Chess {
  void setColor(String color);
  String getColor();
  void display(Point p);
}
class ConcreteChess implements Chess{
  private String color;
  
 public ConcreteChess(String color) {
   this.color = color;
  }

 @Override
 public void setColor(String color) {
  this.color=color;
 }

 @Override
 public String getColor() {
  return this.color;
 }

 @Override
 public void display(Point p) {
  System.out.println(color+"棋"+"在("+p.getX()+","+p.getY()+")点显示");
 }
}

/**
 * 享元工厂
 * @author 小帆敲代码
 *
 */
public class FlyWeightFactory {
  //享元池
 private static  Map<String,Chess> map=new HashMap<String,Chess>();
 public static Chess getChess(String color) {
  if(!map.containsKey(color)) {
   map.put(color, new ConcreteChess(color));
  }
  return map.get(color);
 }
}

public class Client {
  public static void main(String[] args) {
     Chess c1=FlyWeightFactory.getChess("黑");
     Chess c2=FlyWeightFactory.getChess("黑");
     System.out.println(c1);
     System.out.println(c2);
     System.out.println("增加外部状态-----");
     c1.display(new Point(10,10));
     c2.display(new Point(15,15));
  }
}