Algorithms - Priority Queue - 优先队列

Priority queue - 优先队列

相关概念
    Priority queue优先队列是一种用来维护由一组元素构成的集合S的数据结构，
    其中的每一种元素都有一个相关的值,称为关键字（key）。
    一个最大有限队列支持一下操作:
        insert(S,x):把元素x插入到集合S中.
        maximum(S):返回集合S中具有最大关键字的元素.
        extract_max(S):去掉并返回S中具有最大关键字的元素
        increase_key(S,x,k):将集合S中的元素x的关键字值增加到k,这里假设k的值不小于x元素原来的关键字的值

    最大优先队列的应用有很多,其中一个就是在共享计算机系统的作业调度.最大优先队列记录将要执行的各个作业以及他们之间的相对优先级. 当一个作业完成或者被中断后,调度器调用extract_max(S)，从所有作业中,选优具有最高优先级的作业来执行. 在任何时候,调度器都可以调用insert把一个新的作业加入到队列中.

    相应地,最小优先队列支持的操作包括:insert,minimum,extract_min和decrease_key.最小优先队列可以被用于基于事件驱动的模拟器.队列中保存要模拟的事件,每个事件都有一个发生时间作为其关键字.

    事件必须按照发生的时间顺序进行模拟,因为某一事件的模拟结果可能会触发其他事件的模拟. 在每一步,模拟程序调用extract_min来获得下一个要模拟的事件.当一个新事件产生时,模拟器通过调用insert将其插入到最小优先级队列中.

    优先队列可以用堆来实现.对一个像作业调度或时间驱动模拟器这样的程序来说,优先队列的元素对应着应用程序中的对象.

Python programming

# 优先队列是基于最大堆实现的.
import heap_sorting    # heap_sorting 模块代码位于： https://www.cnblogs.com/zzyzz/p/12869256.html

def heap_maximum(A):
    return A[0]

def heap_extract_max(A, heap_size):    # heap_size 是堆的一个属性, 这里通过一个函数参数的形式实现.
    if heap_size < 1:
        print('error - heap underflow')
        return False
    max = A.pop(0)
    heap_size -= 1
    heap_sorting.max_heapify(A,1,heap_size)
    return max

if __name__ == '__main__':
    A = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
    print('Before', A)
    heap_extract_max(A, 10)
    print('After', A)

结果打印:
   Before [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
   After [14, 10, 8, 7, 9, 3, 2, 4, 1]

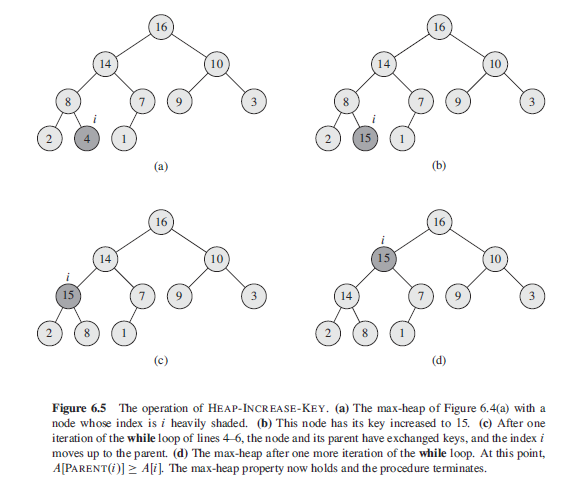
def heap_increase_key(A, i, key):
    if key < A[i-1]:
        print('error - new key is smaller than current key')
        return False
    # 最大堆 A 中的第 i 个元素 A[i-1] 首先被替换成待插入的元素 key
    A[i-1] = key

    # 新插入的元素会不断地与其父结点进行比较, 如果当前元素 key 比较大, 则与其父结点进行交换, 更新 i 的值后继续比较. 直到当前元素 key 小于其父结点的时候终止循环.
    while i > 1 and A[heap_sorting.parent(i)-1] < A[i-1]:
        print(A[heap_sorting.parent(i) - 1], A[i - 1])
        A[i-1], A[heap_sorting.parent(i)-1] = A[heap_sorting.parent(i)-1], A[i-1]
        i = heap_sorting.parent(i)
        print('i',i)
        print('A',A)

if __name__ == '__main__':
    A = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
    print('Before', A)
    heap_increase_key(A,9,15)   # 将 15 插入到最大堆 A 中. 然后加工新的数组为新的最大堆.
    print('After', A)

结果打印:
Before [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
8 15    # 第一次循环的 parent 和 key
i 4       # parent < key, 更新 i
A [16, 14, 10, 15, 7, 9, 3, 2, 8, 1]  # 第一次循环后得到的新数组

14 15  # 第二次循环的 parent 和 key
i 2       # parent < key, 更新 i
A [16, 15, 10, 14, 7, 9, 3, 2, 8, 1]  #  # 第二次循环后得到的新数组
After [16, 15, 10, 14, 7, 9, 3, 2, 8, 1]  # 循环退出后的得到新数组即为新的最大堆

def max_heap_insert(A, key, heap_size):
    heap_size += 1
    A.insert(heap_size-1, -float('inf'))
    print(A)
    heap_increase_key(A, heap_size, key)

if __name__ == '__main__':
    A = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
    print('Before', A)
    max_heap_insert(A,13,10)
    print('After', A)

结果打印:
Before [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
[16, 14, 10, 8, 7, 9, 3, 2, 4, 1, -inf]     # 先在对应的位置上设置一个 sentinel
7 13                                                  # parent < key
i 5                                                     # 交换 parent 和 key 后更新 i
A [16, 14, 10, 8, 13, 9, 3, 2, 4, 1, 7]    # 交换后新的数组
After [16, 14, 10, 8, 13, 9, 3, 2, 4, 1, 7]    # 循环退出后的结果

Reference,

　　1. Introduction to algorithms