hdu 1950 Bridging signals 求最长子序列 （ 二分模板 ）

Bridging signals

Time Limit: 5000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4452    Accepted Submission(s): 2769

Problem Description

'Oh
no, they've done it again', cries the chief designer at the Waferland
chip factory. Once more the routing designers have screwed up
completely, making the signals on the chip connecting the ports of two
functional blocks cross each other all over the place. At this late
stage of the process, it is too
expensive to redo the routing.
Instead, the engineers have to bridge the signals, using the third
dimension, so that no two signals cross. However, bridging is a
complicated operation, and thus it is desirable to bridge as few
signals as possible. The call for a computer program that finds the
maximum number of signals which may be connected on the silicon surface
without rossing each other, is imminent. Bearing in mind that there may
be housands of signal ports at the boundary of a functional block, the
problem asks quite a lot of the programmer. Are you up to the task?

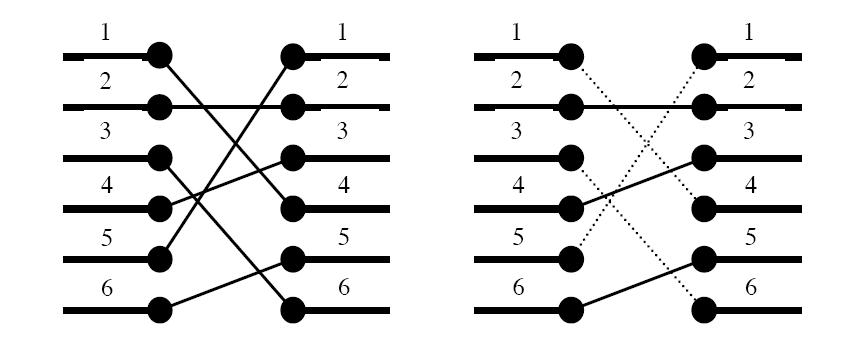
Figure
1. To the left: The two blocks' ports and their signal mapping
(4,2,6,3,1,5). To the right: At most three signals may be routed on the
silicon surface without crossing each other. The dashed signals must be
bridged.

A typical situation is schematically depicted in figure
1. The ports of the two functional blocks are numbered from 1 to p,
from top to bottom. The signal mapping is described by a permutation of
the numbers 1 to p in the form of a list of p unique numbers in the
range 1 to p, in which the i:th number pecifies which port on the right
side should be connected to the i:th port on the left side.
Two signals cross if and only if the straight lines connecting the two ports of each pair do.

 

Input

On
the first line of the input, there is a single positive integer n,
telling the number of test scenarios to follow. Each test scenario
begins with a line containing a single positive integer p<40000, the
number of ports on the two functional blocks. Then follow p lines,
describing the signal mapping: On the i:th line is the port number of
the block on the right side which should be connected to the i:th port
of the block on the left side.

 

Output

For
each test scenario, output one line containing the maximum number of
signals which may be routed on the silicon surface without crossing each
other.

 

Sample Input

4
6 
4 2 6 3 1 5
10
2 3 4 5 6 7 8 9 10 1
8
8 7 6 5 4 3 2 1
9
5 8 9 2 3 1 7 4 6

Sample Output

3
9
1
4

#include<iostream>
#include<algorithm>
using namespace std;
int a[],lis[];
int t,n;
int main()
{
  cin>>t;
  while(t--)
  {
    cin>>n;
    for(int i=;i<=n;i++)//因为upper_bound(),所以从1开始方便
    {
      cin>>a[i];
    }
    int len=;
    for(int i=;i<=n;i++)
    {
      if(a[i]>lis[len])//严格单调
      {
        lis[++len]=a[i];
        continue;
      }
      int t=upper_bound(lis,lis+len,a[i])-lis;//返回第一个比a[i]大的数
      lis[t]=a[i];
    }
    cout<<len<<endl;
  }

  return ;
}