数学--数论--Hdu 5793 A Boring Question （打表+逆元）

There are an equation.

∑0≤k1,k2,⋯km≤n∏1⩽j<m(kj+1kj)%1000000007=?

We define that (kj+1kj)=kj+1!kj!(kj+1−kj)! . And (kj+1kj)=0 while kj+1<kj.

You have to get the answer for each n and m that given to you.

For example,if n=1,m=3,

When k1=0,k2=0,k3=0,(k2k1)(k3k2)=1;

Whenk1=0,k2=1,k3=0,(k2k1)(k3k2)=0;

Whenk1=1,k2=0,k3=0,(k2k1)(k3k2)=0;

Whenk1=1,k2=1,k3=0,(k2k1)(k3k2)=0;

Whenk1=0,k2=0,k3=1,(k2k1)(k3k2)=1;

Whenk1=0,k2=1,k3=1,(k2k1)(k3k2)=1;

Whenk1=1,k2=0,k3=1,(k2k1)(k3k2)=0;

Whenk1=1,k2=1,k3=1,(k2k1)(k3k2)=1.

So the answer is 4.

Input

The first line of the input contains the only integer T,(1≤T≤10000)

Then T lines follow,the i-th line contains two integers n,m,(0≤n≤109,2≤m≤109)

Output

For each n and m,output the answer in a single line.

Sample Input

2

1 2

2 3

Sample Output

3

13

打表很容易看出规律是m0+m1+...+mnm^0+m^1+...+m^nm0+m1+...+mn(鬼扯，我看了好几个小时愣是没看出有什么规律，看完题解还是不知道怎么推出来的，我太难了，这公式推的我服气）

下面是题解，我服我服了，卧槽。

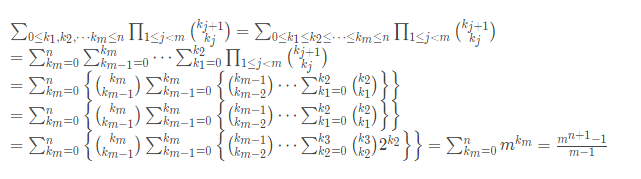
推导公式结束后，你看直接一个逆元完事了，这个题我哭了，比我看到莫比乌斯反演还绝望，卧槽。

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;

long long ksm(long long a, long long n)
{
    long long ans = 1;
    for (; n; n >>= 1)
    {
        if (n & 1)
            ans = ans * a % mod;
        a = a * a % mod;
    }
    return ans;
}
int main()
{
    int T;
    scanf("%d", &T);
    while (T--)
    {
        long long n, m;
        scanf("%lld%lld", &n, &m);
        printf("%lld\n", (ksm(m, n + 1) - 1) * ksm(m - 1, mod - 2) % mod);
    }
    return 0;
}