数据挖掘入门系列教程（十）之k-means算法

简介

这一次我们来讲一下比较轻松简单的数据挖掘的算法——K-Means算法。K-Means算法是一种无监督的聚类算法。什么叫无监督呢？就是对于训练集的数据，在训练的过程中，并没有告诉训练算法某一个数据属于哪一个类别。对于K-Means算法来说，他就是通过某一些骚操作，将一堆“相似”的数据聚集在一起然后当作同一个类别。例如下图：最后将数据聚集成了3个类别。

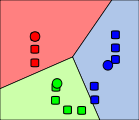
K-Means算法中的$K$就是代表类别的个数，它可以根据用户的需求进行确定，也可以使用某一些方法进行确定（比如说elbow method）。

算法

算法简介

对于给定的样本集$D=\left\{\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \ldots, \boldsymbol{x}_{m}\right\}$，k-means算法针对聚类所得到的簇为$\mathcal{C}=\left\{C_{1}, C_{2}, \ldots, C_{k}\right\}$，则划分的最小化平方误差为：

\[\begin{equation}
E=\sum_{i=1}^{k} \sum_{\boldsymbol{x} \in C_{i}}\left\|\boldsymbol{x}-\boldsymbol{\mu}_{i}\right\|_{2}^{2} \\
其中\boldsymbol{\mu}_{i}=\frac{1}{\left|C_{i}\right|} \sum_{\boldsymbol{x} \in C_{i}}x
\end{equation}
\]

$E$越小则表示数据集样本中相似度越高。我们想得到最小的$E$，但是直接求解并不容易，因此我们采用启发式算法进行求解。

算法流程

算法的流程很简单，如下所示：

选取初始化质心

首先假如我们有如下的数据集，我们随机选取$k$个点（称之为质心，这里$k =3$），也就是下图中红绿蓝三个点。

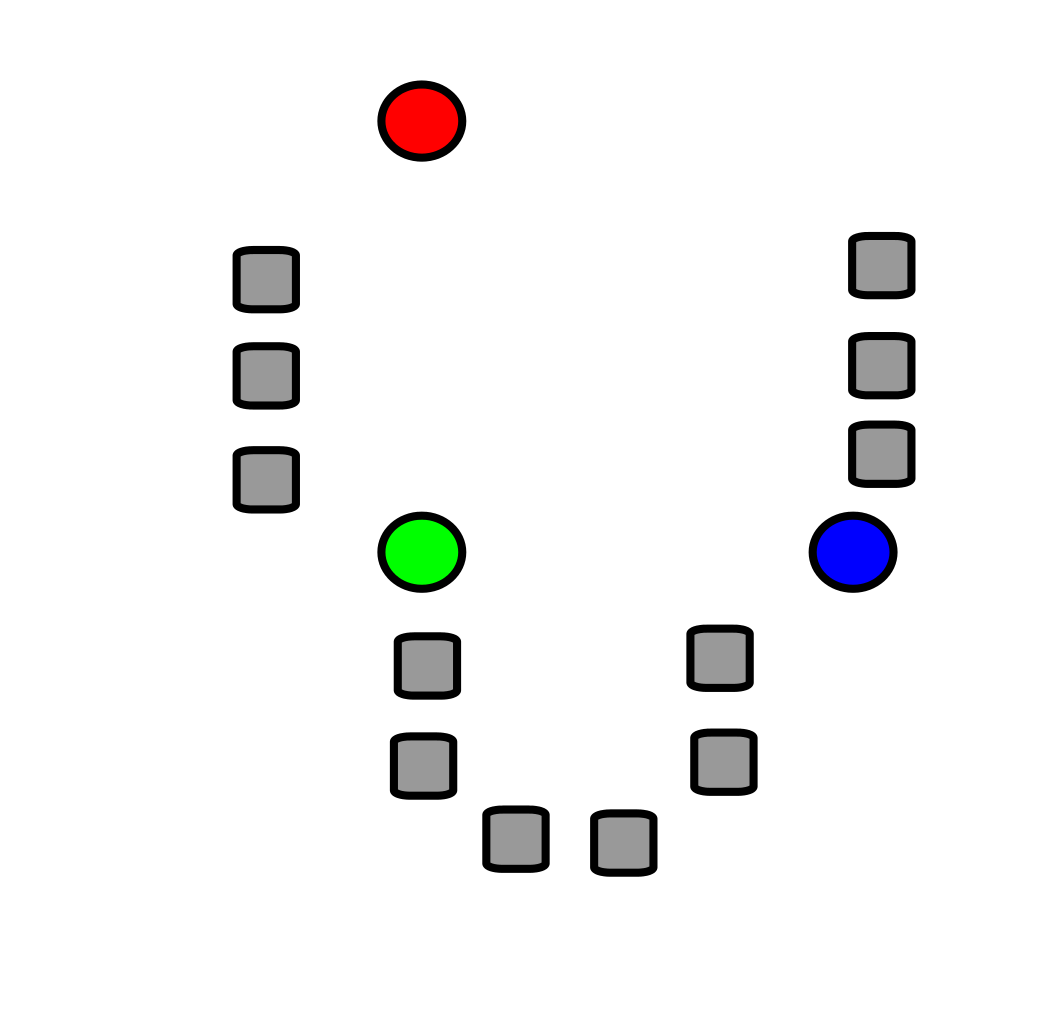
计算数据集样本中其它的点到质心的距离，然后选取最近质心的类别作为自己的类别。

我们可以将其理解为“近朱者赤近墨者黑”，对于样本点来说，哪个质心离我近，我就认谁做“爸爸”。同时对于“距离”，有很多种计算方式，比如说“欧氏距离”，“曼哈顿距离”等等。
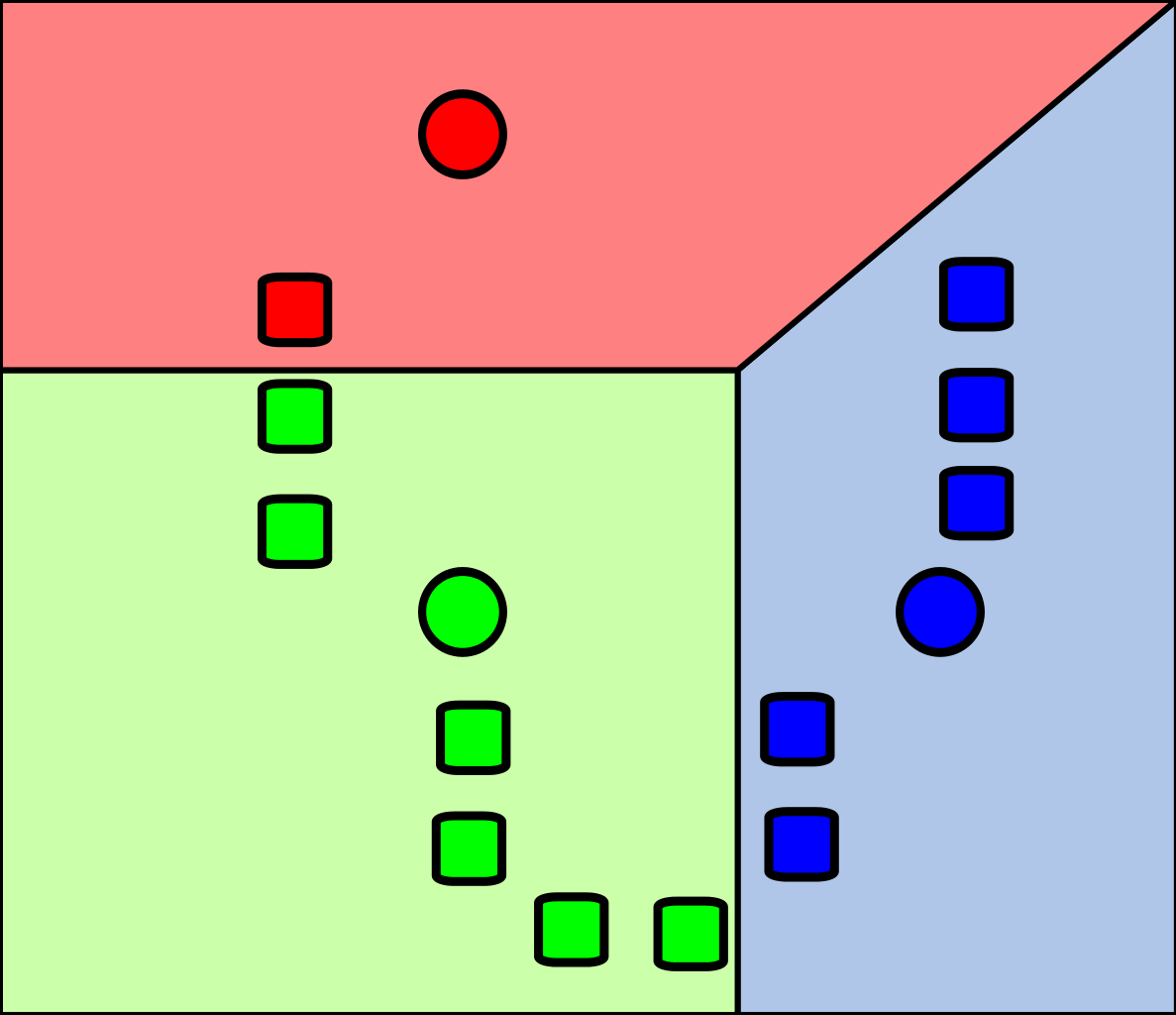
重新计算质心

通过上面的步骤我们就得到了3个簇，然后我们从这三个簇中重新选举质心，也就是我们选举出一个新的“爸爸”，这个"爸爸"可以为样本点（比如说红点），也可以不是样本中的点（比如说蓝点和绿色点）。选举方式很简单，就是计算每一个簇中样本点的平均值。
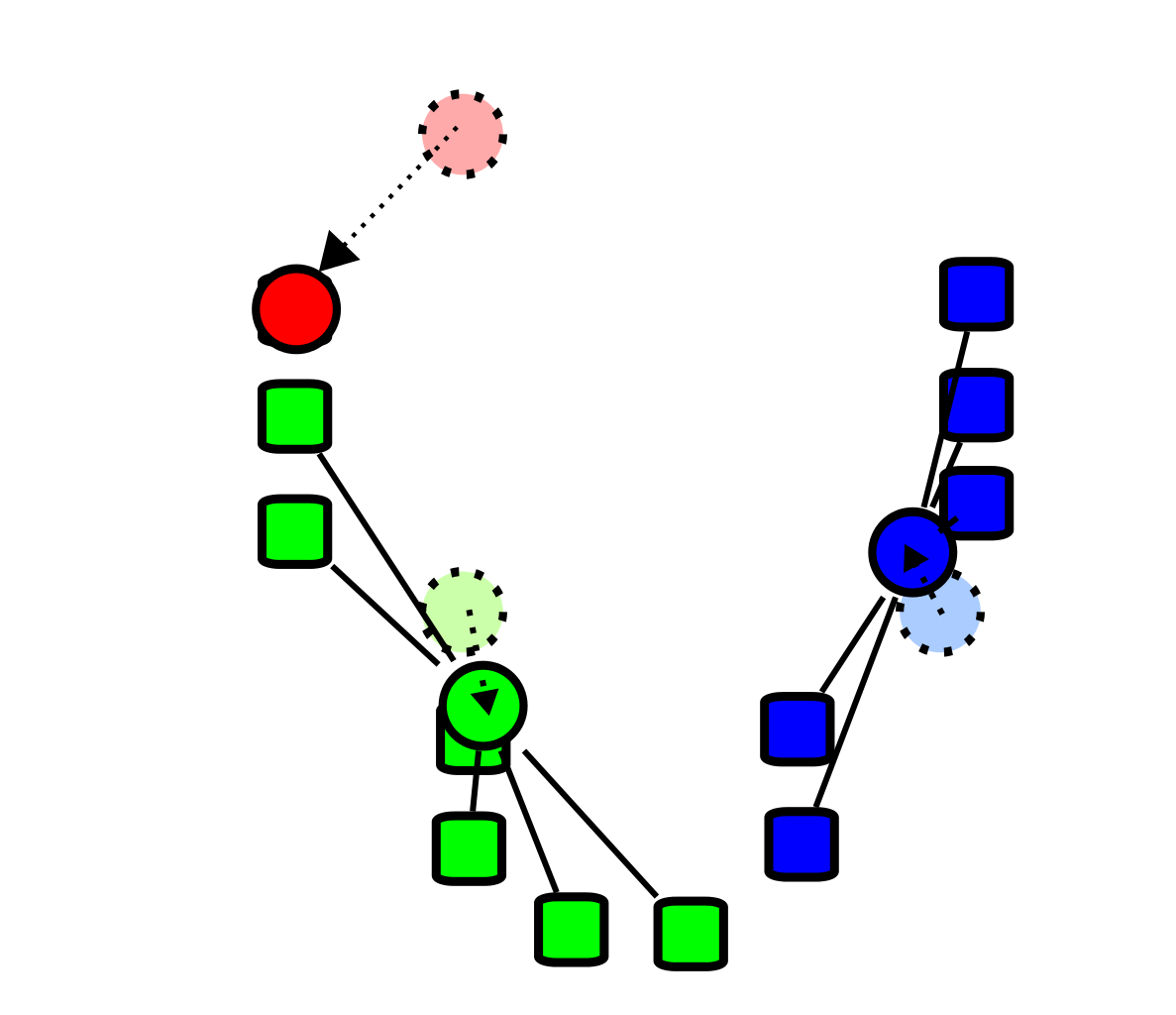
重新进行划分

按照第二步的计算方法重新对样本进行划分。
重复第3，4步骤，直到达到某一个阈值

这个阈值可以是迭代的轮数，也可以是当质心不发生改变的时候或者质心变化的幅度小于某一个值得时候停止迭代。

这里引用《西瓜书》中得算法步骤：

算法gif图如下所示：

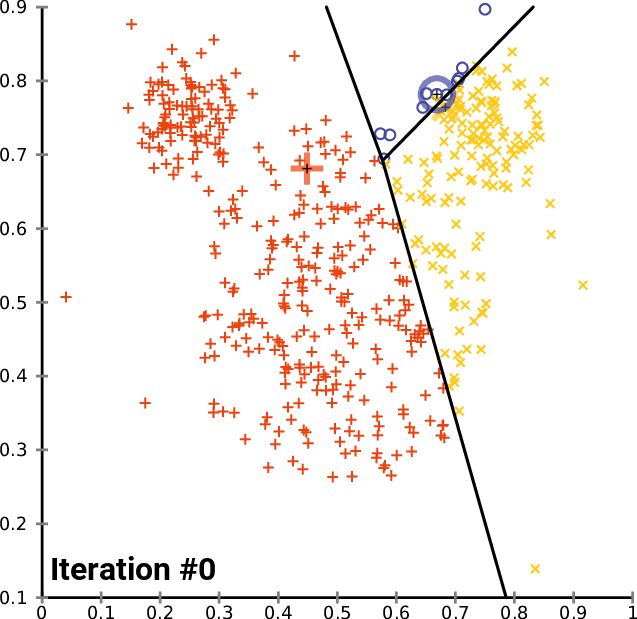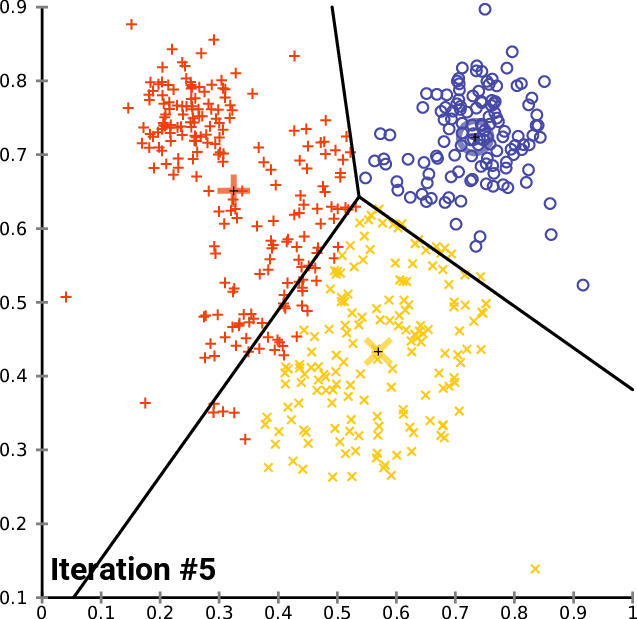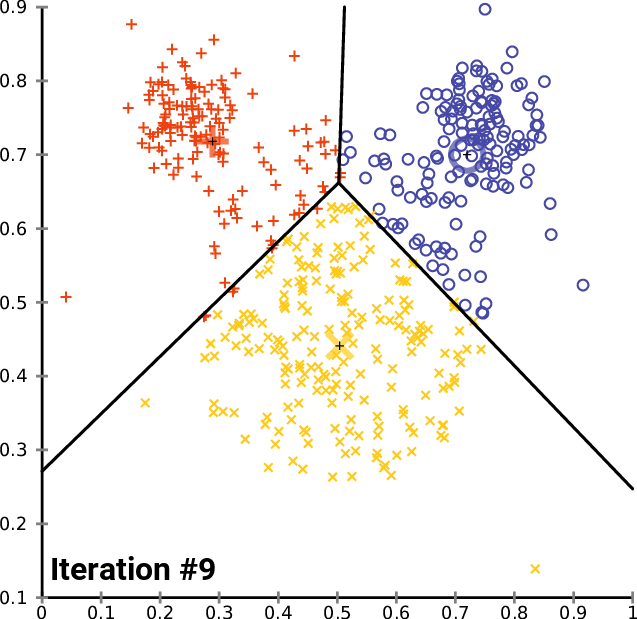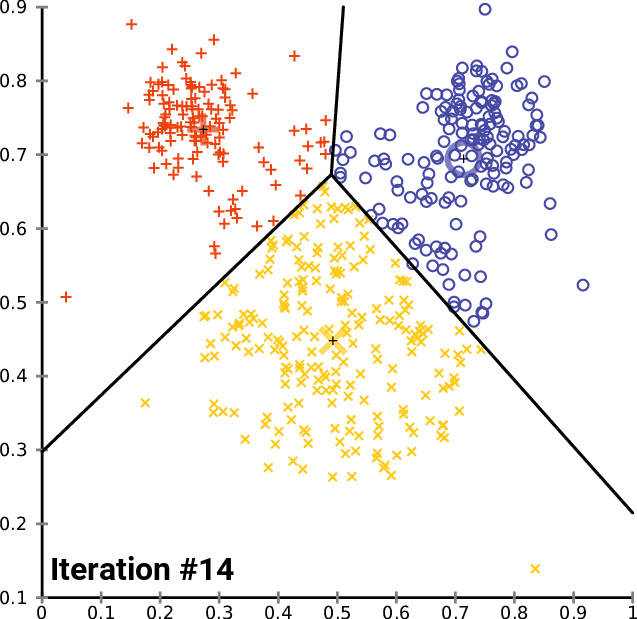
算法的优化

K-Means算法的步骤就如上所示，但是实际上里面还有一些细节可以进行优化。

K-Means++算法

在上面我们讨论了k-means算法的流程，当时我们可以仔细想一想，如果在第一步初始化质心的步骤中，如果质心选择的位置不是特别的好，比如说三个点挨在一起，那这样，我们必定会需要使用大量的迭代步骤。同时它还可能影响着最后簇的结果。为了解决这个误差，我们可以选择一组随机的初始化质心，然后选取最小的$E$值（也就是是最小化平方误差最小）。

当然，我们也有其他的方法。

K-Means++算法与上面传统的K-means算法不同的点就在于它使用了一定的方法使得算法中的第一步（初始化质心）变得比较合理，而不是随机的选择质心。算法的步骤如下：

从输入样本中随机选择一个样本作为质心$\mu_1$
对于数据集中的每一个样本$x_i$，计算它他与已选择的质心$\mu_r$的距离，设样本$x_i$到质心的距离为$D(x_i)$ 【这个距离肯定是离质心的最短距离】，因此$D(x_i) = arg\;min||x_i- \mu_r||_2^2\;\;r=1,2,...k_{selected}$。
选择一个新的数据样本作为新的质心，选择的原则为：$D(x_i)$越大，被选择的概率也就越大。
重复2，3步骤直到选取出$k$个质心。
运行传统k-means算法中的第2，3，4，5步。

K-Means++实际上就是改变了初始化质心的步骤，其他的步骤并没有发生改变。

K-Means算法中距离计算的优化

假设我们有$n+k$个样本（其中有$k$个质心），毋庸置疑，我们需要计算$n$个样本到$k$个质心的距离。这一步我们可以稍微的简化一下。运用三角形两边之和大于第三边我们可以知道：

\[a+b \gt c\\
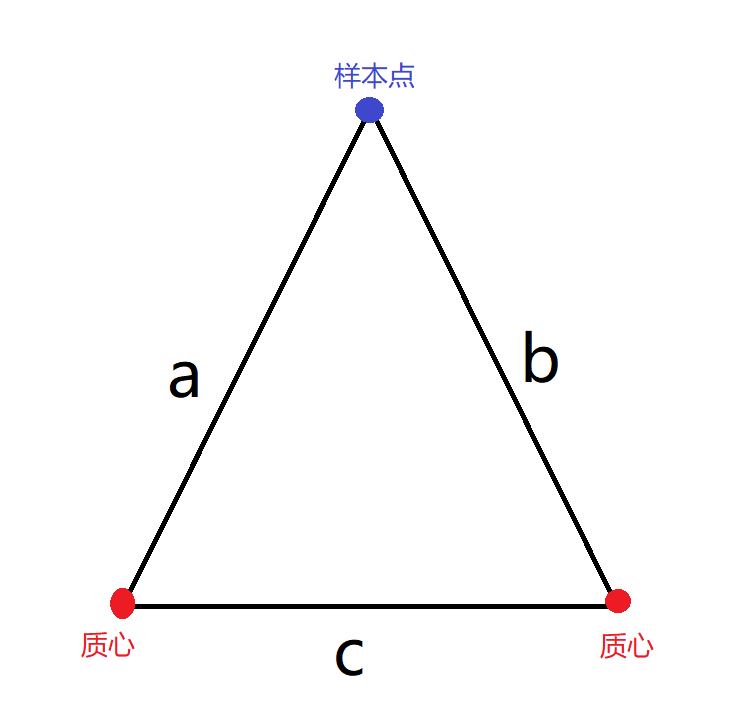
a - b \lt c \\
因此则有：\\
b \geq max\{0,a - c\} \\
若2a \le c,则有\\
a \le b \\
\]

利用上面的这两条规矩，我们就可以在一定程度上简化计算。

K值的确定

前面我们说过$K$值代表着簇数，我们可以按照需求来给定，也可以通过计算的方法给一个比较合理的$K$值。下面就来介绍一下“elbow method”来确定合理的$K$值，关于更多的方法，可以参考一下维基百科。

Elbow Method

Elbow Method原理很简单，我们给定$K$的一个范围，比如说是从0~10，然后我们分别计算每一个K值对应的SSE，也就是前面的最小化平方误差$E$，然后我们再将每一个$K$值对应的SSE画出来。可以很简单的知道，随着$K$值的增大，SSE会趋向于0（假如每一个样本点都是质心，那么对应的距离$E$就是0了）。我们往往希望得到一个较小的SSE，同时保证$K$值也比较小。

我们可以将$K$值对应的SSE图看成一个手臂，则我们选取的$K$的地方就是“肘（elbow）”这个地方，这里是拐弯最大的地方。

基于sklearn的K-Means算法使用

产生数据集

首先的首先，我们需要一个数据集，这里我们使用sklearn中的make_blobs来生成各向同性高斯团簇。然后再将数据进行画图：

import matplotlib.pyplot as plt

import sklearn.datasets as ds

import matplotlib.colors

# 数据集的个数

data_num = 1000

# k值，同时也是生成数据集的中心点

k_num  = 4

# 生成聚类数据，默认n_features为二，代表二维数据，centers表示生成数据集的中心点个数，random_state随机种子

data,y=ds.make_blobs(n_samples=data_num,centers=k_num,random_state=0)

data为二维坐标，y为数据标签，从0到3。画图代码如下：

# 不同的数据簇用不同的颜色表示

data_colors = matplotlib.colors.ListedColormap(['red','blue','yellow','Cyan'])

# data为二维数据

plt.scatter(data[:,0],data[:,1],c=y,cmap=data_colors)

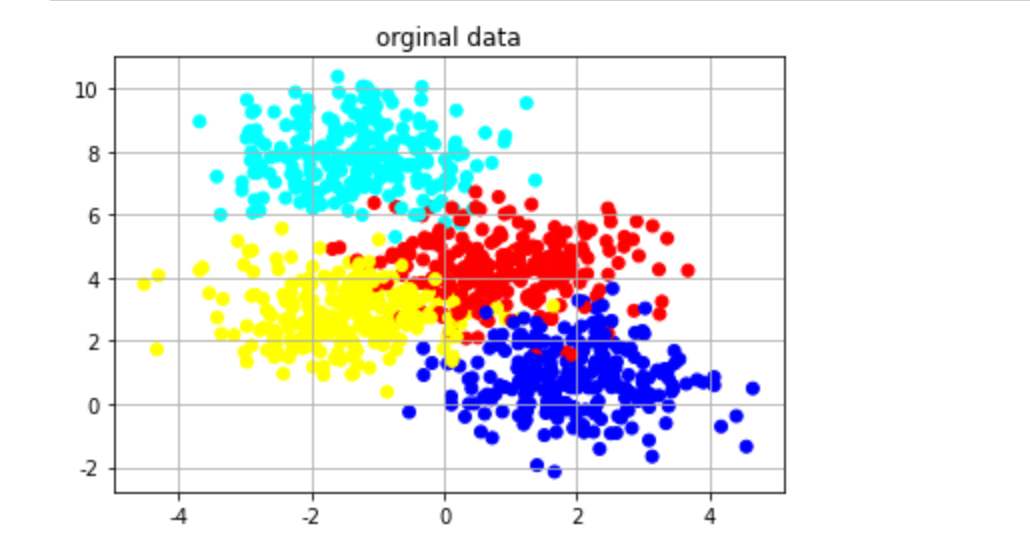
plt.title("orginal data")

plt.grid()

plt.show()

画图如下所示

使用k-means

我们可以使用cluster包下的KMeans来使用k-means算法，具体参数可以看官方文档。

'''

sklearn.cluster.KMeans(

	n_clusters=8,

	init='k-means++',

	n_init=10,

	max_iter=300,

	tol=0.0001,

	precompute_distances='auto',

	verbose=0,

	random_state=None,

	copy_x=True,

	n_jobs=1,

	algorithm='auto' )

参数说明：

(1)n_clusters:簇的个数，也就是k值

(2)init: 初始簇中心的方式，可以为k-means++,也可以为random

(3)n_init: k-means算法在不同随机质心情况下迭代的次数，最后的结果会输出最好的结果

(4)max_iter: k-means算法最大的迭代次数

(5)tol: 关于收敛的相对公差

(8)random_state: 初始化质心的随机种子

(10)n_jobs: 并行工作，-1代表使用所有的处理器

'''

from sklearn.cluster import KMeans

model=KMeans(n_clusters=k_num,init='k-means++')

# 训练

model.fit(data)

# 分类预测

y_pre= model.predict(data)

然后我们可以将预测分类结果画出来：

plt.scatter(data[:,0],data[:,1],c=y_pre,cmap=data_colors)

plt.title("k-means' result")

plt.grid()

plt.show()

总结

当然，k-means对于某一些分类任务还是比较困难，如下：

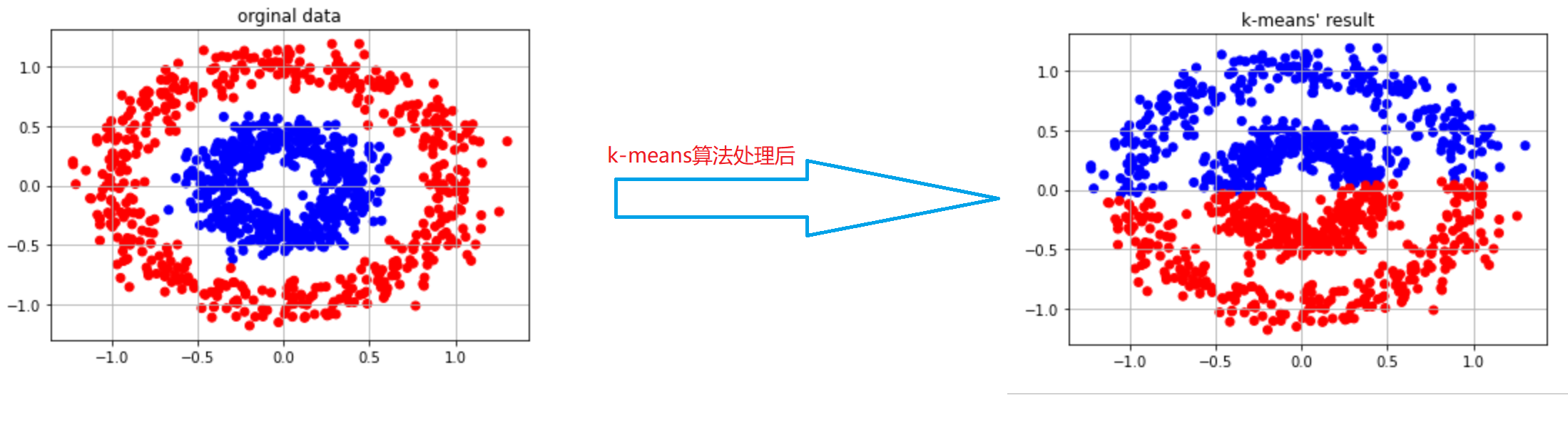
很明显，我们应该将数据分成内圈和外圈，但是呢，使用k-means算法后，将数据集分成了上下两个部分，这样肯定是不对的。

总的来说，k-means算法还是比较简单的，没有什么复杂的地方，也易于实现。

项目地址：Github

参考

k-means clustering
《西瓜书》
K-Means聚类算法原理
Determining the number of clusters in a data set
elbow method