tarjan算法强连通分量的正确性解释+错误更新方法的解释！！！+hdu1269

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1269

以下内容为原创，转载请声明。

强连通分量SCC（Strongly Connected Component）：一个图的子图，如果任何两个点都互相可达且满足最大性，该子图就是原图的SCC。

对于有向图的连通性，tarjan可以说是十分牛逼了，由于tarjan只需要一次dfs就能判断有向图中所有的SCC，所以他的复杂度是O(|V|+|E|)，也就是把每条边和每个点都会检索一遍，是在线性时间能处理出所有的SCC的！下面简单说明求强连通分量的tarjan算法的过程以及正确性。

基础知识：

①、经dfs处理过的点的low值相同的一定属于同一个SCC，这个SCC中第一个被dfs访问的点也就是dfn=low的点一定就是这个SCC中每个点的low值，显而易见。

②、在dfs过程中，dfs进行最深处一定会进入某一个SCC，（尽管在过程中可能会进入其他SCC），下面我会解释

③、标记SCC Number的过程可以用栈实现，因为dfs的过程就是递归，递归和栈非常相似

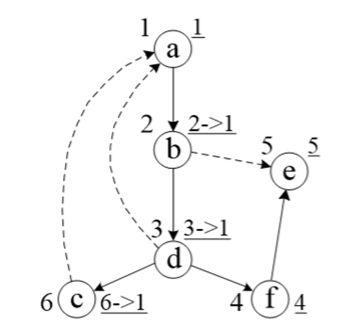
tarjan算法的流程：将每个访问的点入栈，更新low值，直到到达一个点，这个点low值等于dfn值，说明这个点一定是一个SCC的祖先，也就是第一个访问的点，此时这个点一定在栈的底部！！因为是通过dfs退出多次而不弹栈才得到这个low=dfn。我们只要不断弹出l这个SCC的点并标记就可以，直到弹到栈底。我们先看基础知识（2），上图中在访问3的时候进入了4、5结点，也就是其他SCC，到了5的时候，由于low[5]=dfn[5]所以此时弹栈，发现就只有一个5属于这个SCC，4也是同样的过程，直到到了3，进入另一个分支6，这就是我基础知识（2）中的一定会在最终进入一个SCC而且栈底元素就是这个SCC的祖结点。

关于强连通分量处理回退边的方式，我的解释是这样的：

当一个点已经标记过dfn之后，而且这个点在之前没有标记过SCC（因为在dfs过程中会进入并处理其他SCC，若此时有边相连就无需更新，因为回退边所到点的low值一定小于该点的low)就用

①、low[u]=min(low[v],dfn[v])　　②、low[u]=min(low[v],low[u])

来更新low值，其实对于双连通分量来说，这两种更新方式的结果是一样的，但是第一种方法在原理上是错误的！！！！！ 我来举一个例子，又是下面这张图，

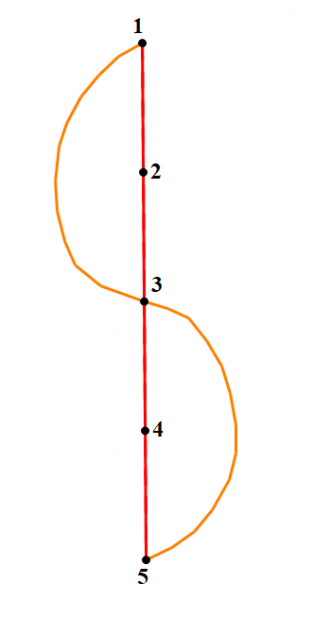
对于第一种我们得出的结果是下面第一张图，而对于第二张我们得到的结果是下面第二张图，我们可以发现，根据tarjan算法的思想，处于同一个强连通分量中的点low值应该是相同的，但是第一种做法中的点的low值是不同的，但是他们得到的结果都是一样的，都是图是强连通的，为什么呢？

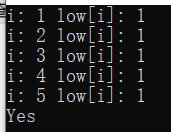
 下面我将证明第一种做法得出正确结果的原因：

由于对于4,5号节点来说，他们的low值为3的时候，都与他们的dfn值不相同（dfn[4]=4&dfn[5]=5），所以他们就会一直在栈中，而栈底也一定是1号结点。4,5号结点没有机会弹出，直到dfs return到1号结点，此时才会弹栈，一直到弹出1号结点为止，这就把栈中的结点4,5弹出了，但是事实上他们的low值是更新错误的。尽管是错误的，但是中途dfs在访问其他SCC的时候（如果有的话，可以参考最上面那张图）已经把其他SCC的点都标记了，此时栈中剩下的只有这一个SCC！！所以最终的结果是相同的，但是！！这种更新方法是错误的！！因为在之后不能通过他们的不同的low值数量去查看SCC的数量，只能从每一次弹栈中给出的SCCNUMBER中得到SCC的信息。而且，这种做法跟tarjan的算法中“每个SCC”的low值是相同的是矛盾的。

看完我的文章能不能支持一下呢

hdu1269代码如下：

 #include<bits/stdc++.h>
 using namespace std;
 typedef unsigned int ui;
 typedef long long ll;
 typedef unsigned long long ull;
 #define pf printf
 #define mem(a,b) memset(a,b,sizeof(a))
 #define prime1 1e9+7
 #define prime2 1e9+9
 #define pi 3.14159265
 #define lson l,mid,rt<<1
 #define rson mid+1,r,rt<<1|1
 #define scand(x) scanf("%llf",&x)
 #define f(i,a,b) for(int i=a;i<=b;i++)
 #define scan(a) scanf("%d",&a)
 #define mp(a,b) make_pair((a),(b))
 #define P pair<int,int>
 #define dbg(args) cout<<#args<<":"<<args<<endl;
 #define inf 0x3f3f3f3f
 inline int read(){
     int ans=,w=;
     char ch=getchar();
     while(!isdigit(ch)){if(ch=='-')w=-;ch=getchar();}
     while(isdigit(ch))ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
     return ans*w;
 }
 const int maxn=1e5+;
 int n,m,t;
 int head[maxn],nxt[maxn],low[maxn],sccno[maxn],dfn[maxn],id;
 struct node{
     int u,v;
 }p[maxn*];
 int e=;
 int cnt;
 stack<int> sk;
 void addedge(int u,int v)
 {
     p[e].u=u;
     p[e].v=v;
     nxt[e]=head[u];
     head[u]=e++;
 }
 void tarjan(int u)
 {
     low[u]=dfn[u]=++id;
     sk.push(u);//将结点编号压栈
     for(int i=head[u];~i;i=nxt[i])
     {
         int v=p[i].v;
         if(!dfn[v])
         {
             tarjan(v);
             low[u]=min(low[u],low[v]);
         }
         else if(!sccno[v])//回退边且边终点没有标记SCC
             low[u]=min(low[u],low[v]);
     }
     if(low[u]==dfn[u])
     {
         cnt++;//连通分量的数量增加,对每个点这个if语句只执行一次
         while()
         {
             int v=sk.top();
             sk.pop();
             sccno[v]=cnt;
             if(u==v)break;
         }
      }
 }
 int main()
 {
     freopen("input.txt","r",stdin);
     //freopen("output.txt","w",stdout);
     std::ios::sync_with_stdio(false);
     while(scanf("%d%d",&n,&m)==)
     {
         if(n==&&m==)break;
         e=;cnt=;
         mem(head,-);mem(nxt,-);
         while(!sk.empty())sk.pop();
         int x,y;
         f(i,,m)
         {
             x=read();
             y=read();
             addedge(x,y);
         }
         mem(dfn,);
         id=;
         mem(sccno,);
         mem(low,);
         f(i,,n)
         {
             if(!dfn[i])
                 tarjan(i);
         }
         f(i,,n)dbg(low[i]);
         if(cnt==)pf("Yes\n");
         else pf("No\n");
      }
 }