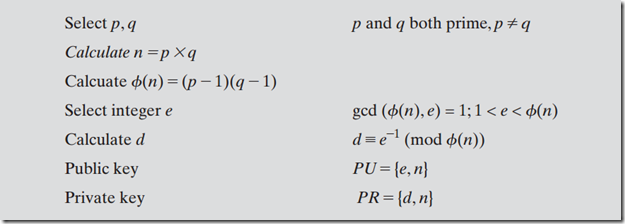RSA加密算法c++简单实现
RSA是一种非对称加密算法,在公开密钥和电子商业中RSA被广泛使用。它是基于一个很简单的数论事实,两个素数相乘很容易,对两素数乘积因式分解很困难。原理就不再阐述了,我谈谈算法的编程实现过程。
一、RSA加密和解密过程是基于以下形式,其中明文为M,密文为C,公匙PU={e, n},密匙PR={d, n}。
1、准备工作,选择两个大素数p和q,计算p和q的乘积n,计算p-1和q-1的乘积,选择一个与p-1和q-1乘积互质的数e,计算出d
2、加密过程
3、解密过程
程序没有生成大素数,只是列出1000以内的素数,随机取两个素数p和q,利用欧德里德扩展算法计算出e和d,用反复平方法求数的幂
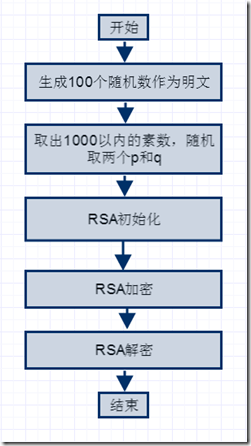
二、程序流程图
三、程序源码
#include <iostream>
#include <cmath>
#include <cstring>
#include <ctime>
#include <cstdlib>
using namespace std; int Plaintext[];//明文
long long Ciphertext[];//密文
int n, e = , d; //二进制转换
int BianaryTransform(int num, int bin_num[])
{ int i = , mod = ; //转换为二进制,逆向暂存temp[]数组中
while(num != )
{
mod = num%;
bin_num[i] = mod;
num = num/;
i++;
} //返回二进制数的位数
return i;
} //反复平方求幂
long long Modular_Exonentiation(long long a, int b, int n)
{
int c = , bin_num[];
long long d = ;
int k = BianaryTransform(b, bin_num)-; for(int i = k; i >= ; i--)
{
c = *c;
d = (d*d)%n;
if(bin_num[i] == )
{
c = c + ;
d = (d*a)%n;
}
}
return d;
} //生成1000以内素数
int ProducePrimeNumber(int prime[])
{
int c = , vis[];
memset(vis, , sizeof(vis));
for(int i = ; i <= ; i++)if(!vis[i])
{
prime[c++] = i;
for(int j = i*i; j <= ; j+=i)
vis[j] = ;
} return c;
} //欧几里得扩展算法
int Exgcd(int m,int n,int &x)
{
int x1,y1,x0,y0, y;
x0=; y0=;
x1=; y1=;
x=; y=;
int r=m%n;
int q=(m-r)/n;
while(r)
{
x=x0-q*x1; y=y0-q*y1;
x0=x1; y0=y1;
x1=x; y1=y;
m=n; n=r; r=m%n;
q=(m-r)/n;
}
return n;
} //RSA初始化
void RSA_Initialize()
{
//取出1000内素数保存在prime[]数组中
int prime[];
int count_Prime = ProducePrimeNumber(prime); //随机取两个素数p,q
srand((unsigned)time(NULL));
int ranNum1 = rand()%count_Prime;
int ranNum2 = rand()%count_Prime;
int p = prime[ranNum1], q = prime[ranNum2]; n = p*q; int On = (p-)*(q-); //用欧几里德扩展算法求e,d
for(int j = ; j < On; j+=)
{
int gcd = Exgcd(j, On, d);
if( gcd == && d > )
{
e = j;
break;
} } } //RSA加密
void RSA_Encrypt()
{
cout<<"Public Key (e, n) : e = "<<e<<" n = "<<n<<'\n';
cout<<"Private Key (d, n) : d = "<<d<<" n = "<<n<<'\n'<<'\n'; int i = ;
for(i = ; i < ; i++)
Ciphertext[i] = Modular_Exonentiation(Plaintext[i], e, n); cout<<"Use the public key (e, n) to encrypt:"<<'\n';
for(i = ; i < ; i++)
cout<<Ciphertext[i]<<" ";
cout<<'\n'<<'\n';
} //RSA解密
void RSA_Decrypt()
{
int i = ;
for(i = ; i < ; i++)
Ciphertext[i] = Modular_Exonentiation(Ciphertext[i], d, n); cout<<"Use private key (d, n) to decrypt:"<<'\n';
for(i = ; i < ; i++)
cout<<Ciphertext[i]<<" ";
cout<<'\n'<<'\n';
} //算法初始化
void Initialize()
{
int i;
srand((unsigned)time(NULL));
for(i = ; i < ; i++)
Plaintext[i] = rand()%; cout<<"Generate 100 random numbers:"<<'\n';
for(i = ; i < ; i++)
cout<<Plaintext[i]<<" ";
cout<<'\n'<<'\n';
} int main()
{
Initialize(); while(!e)
RSA_Initialize(); RSA_Encrypt(); RSA_Decrypt(); return ;
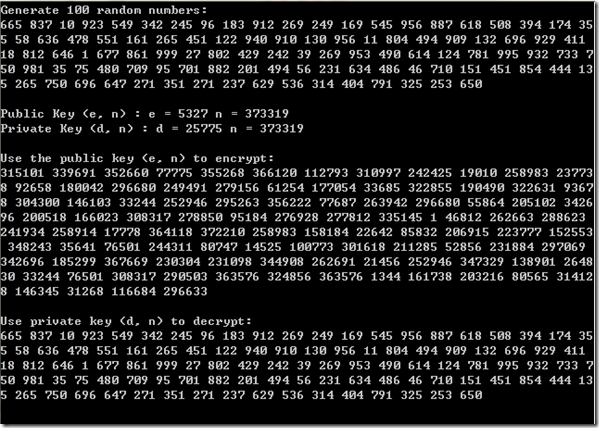
}四、运行结果
RSA加密算法c++简单实现的更多相关文章
- RSA加密算法的简单案例
RSA加密算法是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的绝大多数密码攻击. 那关于RSA加密算法有哪些应用呢?以下举一个数据库身份验证的案例. 在使用数据集进行身份认证时,密码存在数据 ...
- 加密算法——RSA算法(c++简单实现)
RSA算法原理转自:https://www.cnblogs.com/idreamo/p/9411265.html C++代码实现部分为本文新加 RSA算法简介 RSA是最流行的非对称加密算法之一.也被 ...
- 用实例讲解RSA加密算法(精)
RSA是第一个比较完善的公开密钥算法,它既能用于加密,也能用于数字签名.RSA以它的三个发明者Ron Rivest, Adi Shamir, Leonard Adleman的名字首字母命名,这个算法经 ...
- RSA加密算法的加密与解密
转发原文链接:RSA加密算法加密与解密过程解析 1.加密算法概述 加密算法根据内容是否可以还原分为可逆加密和非可逆加密. 可逆加密根据其加密解密是否使用的同一个密钥而可以分为对称加密和非对称加密. 所 ...
- 轻松学习RSA加密算法原理
转自:http://blog.csdn.net/sunmenggmail/article/details/11994013 http://blog.csdn.net/q376420785/articl ...
- RSA加密算法原理及RES签名算法简介
第一部分:RSA算法原理与加密解密 一.RSA加密过程简述 A和B进行加密通信时,B首先要生成一对密钥.一个是公钥,给A,B自己持有私钥.A使用B的公钥加密要加密发送的内容,然后B在通过自己的私钥解密 ...
- 浅谈RSA加密算法
一.什么是非对称加密 1.加密的密钥与加密的密钥不相同,这样的加密算法称之为非对称加密 2.密钥分为:公钥,私钥 公钥:可以对外给任何人的加密和解密的密码,是公开的 私钥:通过私钥可以生成公钥,但从 ...
- 轻松学习RSA加密算法原理 (转)
轻松学习RSA加密算法原理 (转) http://blog.csdn.net/q376420785/article/details/8557266 http://www.ruanyifeng.com/ ...
- [转] 用实例给新手讲解RSA加密算法
http://www.cfca.com.cn/zhishi/wz-012.htm PS: 通常公钥对数据加密,私钥对数据解密:私钥对数据签名,公钥对数据签名进行认证 RSA加密算法是最常用的非对称加密 ...
随机推荐
- 【opencv源码解析】 三、resize
resize.cpp void cv::resize( InputArray _src, OutputArray _dst, Size dsize, double inv_scale_x, doubl ...
- vue-cli之加载ico文件
vue-cli之加载ico文件 vue-cli加载ico文件需要在vue.config.js设置ico加载,代码如下: module.exports = { publicPath: process.e ...
- jQuery 手写菜单(ing)
菜单支持多级 直接上代码 <!DOCTYPE html> <html lang="en"> <head> <meta charset=&q ...
- 前端通过url下载文件方法
前端通过url下载文件方法 产生背景 浏览器通过url下载文件,当浏览器识别出资深能播放的资源文件,就不会走下载流程,会直接打开 解决方法 1.让后台转成请求的方式,输出文件流(如果想实现批量下载-因 ...
- ESP8266开发环境、编译、烧录
官方地址 中:http://www.espressif.com/zh-hans/support/download/overview?keys=&field_type_tid[]=14 英:ht ...
- JPA中的复杂查询
JPQL全称Java Persistence Query Language 基于首次在EJB2.0中引入的EJB查询语言(EJB QL),Java持久化查询语言(JPQL)是一种可移植的查询语言,旨在 ...
- 将windows当做linux/Mac来用 scoop强大的包管理工具
在Linux中有apt-get.yum这些包安装管理 安装相当方便:如ubuntu安装一个mysql5.7,只需要一个简单的命令: apt-get 而在windows中需要在MySQL官网下载对应版本 ...
- 谷歌浏览器安装xpath使用
一.Xpath-helper插件说明 谷歌浏览的插件,目的是可以定位到具体的元素中,实时验证xpath是不是正确 谷歌插件下载位置:https://chrome.google.com/webstore ...
- 实时跟踪之TRACA
背景: 目前,在实时跟踪领域存在着越来越多的先进方法,同时也极大地促进了该领域的发展.主要有两种不同的基于深度学习的跟踪方法:1.由在线跟踪器组成,这些跟踪器依赖网络连续的微调来学习目标的变化外观,精 ...
- AJAX配置csrf
// 从COokie取CSRF TOKEN的值 function getCookie(name) { var cookieValue = null; if (document.cookie & ...