剑指offer35：数组中的逆序对

1 题目描述

　　在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

2 思路和方法

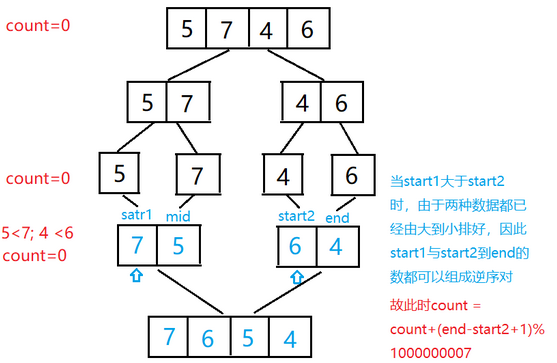
　　利用归并排序的思想，先把数组分隔成子数组，先统计出子数组内部的逆序对的数目，然后再统计出两个相邻子数组之间的逆序对的数目。注意在合并两个已排序的子数组后，要更新数组。O(n*log(n))。

3 C++核心代码

 class Solution {
 public:
     int InversePairs(vector<int> data) {
         if(data.size() <= )
             return ;
         int count = ;
         vector<int> copy(data); // 初始化
         InversePairsCore(data, copy, , data.size()-,count);
         return count;
     }

     // 归并
     void InversePairsCore(vector<int> &data, vector<int> &copy, int start, int end, int &count){
         if(start>=end){
             return;
         }
         int mid = (start + end) /;
         InversePairsCore(data,copy,start,mid,count);
         InversePairsCore(data,copy,mid+,end,count);

         int copyIndex = end; // 将较大数字从后往前复制到辅助数组
         int i = mid;    // 前半段最后一个元素下标
         int j = end;    // 后半段最后一个元素下标
         while (i>=start && j>=mid+) {
             if (data[j] < data[i]){     // 逆序
                 count += j - mid;
                 count %= ;    // 取模防止逆序对溢出
                 copy[copyIndex--] = data[i--];
             } else{
                 copy[copyIndex--] = data[j--];
             }
         }

         while (i>=start)
             copy[copyIndex--] = data[i--];

         while (j>=mid+)
             copy[copyIndex--] = data[j--];

         for (int k = start; k <= end; ++k)
             data[k] = copy[k];

     }
 };

4 C++完整代码

 #include<iostream>
 using namespace std;
 //数组中的逆序对
 long long GetMergePairsBetween(int* arr,int* copy,int start,int mid,int end)
 {
     //合并两个子数组，并计算逆序对个数
     int final1 = mid;//第一个数组的最后一位
     int final2 = end;//第二个数组的最后一位
     int index = end;//辅助数组的最后一位
     long long count = ;
     while(final1 >= start && final2 >= mid+)//两个数组都没有处理完
     {
        if(arr[final1] > arr[final2])
        {
            //如果第一个数组的元素大于第二个数组的任何元素，
            //则第一个数组的元素一定大于第个数组中final2之前的所有元素
            count += (final2 - mid);
            //将final1处的元素拷贝至copy数组
            //index和final1都向前移动
            copy[index--] = arr[final1--];
        }
        else
        {
            //第一个数组的元素小于第二个数组的元素
            //第二个数组的元素拷贝至copy数组
            //并将index和final2前移
            copy[index--] = arr[final2--];
        }
     }
     while(final1 >= start)//第一个数组的元素没有处理完
     {
        copy[index--] = arr[final1--];
     }
     while(final2 >= mid + )//第一个数组的元素没有处理完
     {
        copy[index--] = arr[final2--];
     }
     for(int i = end; i > index;i--)
         arr[i] = copy[i];
     return count;
 }
 long long GetMergePairs(int* arr,int* copy,int start,int end)
 {
     long long ret = ;
     if(start < end)
     {
        int mid = start + ((end - start)>>);
        ret += GetMergePairs(arr,copy,start,mid);
        ret += GetMergePairs(arr,copy,mid+,end);
        ret += GetMergePairsBetween(arr,copy,start,mid,end);
     }
     return ret;
 }
 long long GetTotalPairs(int arr[],int n)
 {
     if(arr == NULL || n < )
        return ;
     int* copy = new int[n];
     long long sum = GetMergePairs(arr,copy,,n-);
     delete[] copy;
     return sum;
 }
 int main()
 {
     int arr[] = {,,,};
     int ret = GetTotalPairs(arr,sizeof(arr)/sizeof(arr[]));
     cout<<ret<<endl;
     system("pause");
     return ;
 }

参考资料

https://blog.csdn.net/zjwreal/article/details/88769617

https://blog.csdn.net/DERRANTCM/article/details/46761051（图）

https://blog.csdn.net/peiyao456/article/details/54645952（完整代码）