算法详解之Tarjan

“tarjan陪伴强联通分量
生成树完成后思路才闪光
欧拉跑过的七桥古塘
让你 心驰神往”----《膜你抄》

一、tarjan求强连通分量

什么是强连通分量？

引用来自度娘的一句话：

“有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。

如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。”

一脸懵逼......不过倒也不难理解。

反正就是在图中找到一个最大的图，使这个图中每个两点都能够互相到达。这个最大的图称为强连通分量，同时一个点也属于强连通分量。

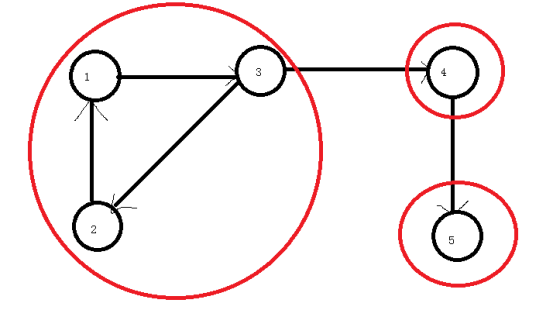
如图中强连通分量有三个：1-2-3,4,5

强连通分量怎么找？

噫......当然，通过肉眼可以很直观地看出1-2-3是一组强连通分量，但很遗憾，机器并没有眼睛，所以该怎么判断强连通分量呢？

如果仍是上面那张图，我们对它进行dfs遍历。

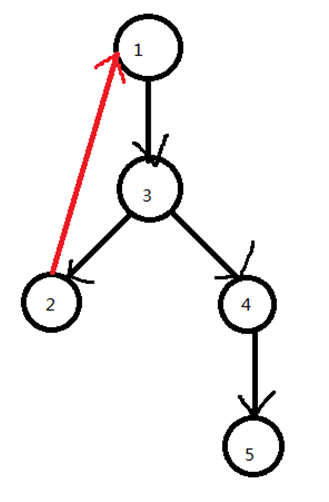
可以注意到红边非常特别，因为如果按照遍历时间来分类的话，其他边都指向在自己之后被遍历到的点，而红边指向的则是比自己先被遍历到的点。

如果存在这么一条边，那么我们可以yy一下，emmmm.......

从一个点出发，一直向下遍历，然后忽得找到一个点，那个点竟然有条指回这一个点的边！

那么想必这个点能够从自身出发再回到自身

想必这个点和其他向下遍历的该路径上的所有点构成了一个环，

想必这个环上的所有点都是强联通的。

但只是强联通啊，我们需要求的可是强连通分量啊......

那怎么办呢？

我们还是yy出那棵dfs树

不妨想一下，什么时候一个点和他的所有子孙节点中的一部分构成强连通分量？

他的子孙再也没有指向他的祖先的边，却有指向他自己的边

因为只要他的子孙节点有指向祖先的边，显然可以构成一个更大的强联通图。

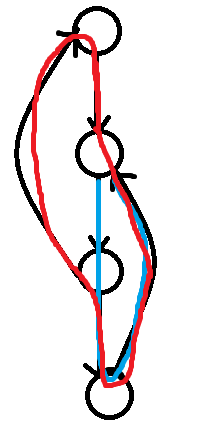
比如说图中红色为强连通分量，而蓝色只是强联通图

那么我们只需要知道这个点u下面的所有子节点有没有连着这个点的祖先就行了。

但似乎还有一个问题啊......

我们怎么知道这个点u它下面的所有子节点一定是都与他强联通的呢？

这似乎是不对的，这个点u之下的所有点不一定都强联通

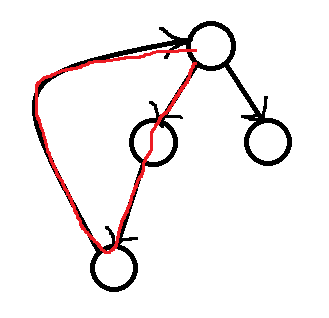
那么怎么在退回到这个点的时候，知道所有和这个点u构成强连通分量的点呢？

开个栈记录就行了

什么？！这么简单？

没错_{就是这么简单}

如果在这个点之后被遍历到的点已经能与其下面的一部分点（也可能就只有他一个点）已经构成强连通分量，即它已经是最大的。

那么把它们一起从栈里弹出来就行了。

所以最后处理到点u时如果u的子孙没有指向其祖先的边，那么它之后的点肯定都已经处理好了，一个常见的思想，可以理解一下。

所以就可以保证栈里留下来u后的点都是能与它构成强连通分量的。

似乎做法已经明了了，用程序应该怎么实现呢？

所以为了实现上面的操作，我们需要一些辅助数组

(1)、dfn[ ]，表示这个点在dfs时是第几个被搜到的。
(2)、low[ ]，表示这个点以及其子孙节点连的所有点中dfn最小的值
(3)、stack[ ]，表示当前所有可能能构成是强连通分量的点。
(4)、vis[ ]，表示一个点是否在stack[ ]数组中。

那么按照之上的思路，我们来考虑这几个数组的用处以及tarjan的过程。

假设现在开始遍历点u：

(1)、首先初始化dfn[u]=low[u]=第几个被dfs到

dfn可以理解，但为什么low也要这么做呢？

因为low的定义如上，也就是说如果没有子孙与u的祖先相连的话，dfn[u]一定是它和它的所有子孙中dfn最小的（因为它的所有子孙一定比他后搜到）。

(2)、将u存入stack[ ]中，并将vis[u]设为true

stack[ ]有什么用？

如果u在stack中，u之后的所有点在u被回溯到时u和栈中所有在它之后的点都构成强连通分量。

(3)、遍历u的每一个能到的点，如果这个点dfn[ ]为0，即仍未访问过，那么就对点v进行dfs，然后low[u]=min{low[u],low[v]}

low[ ]有什么用？

应该能看出来吧，就是记录一个点它最大能连通到哪个祖先节点（当然包括自己）

如果遍历到的这个点已经被遍历到了，那么看它当前有没有在stack[ ]里,如果有那么low[u]=min{low[u],low[v]}

如果已经被弹掉了，说明无论如何这个点也不能与u构成强连通分量，因为它不能到达u

如果还在栈里，说明这个点肯定能到达u，同样u能到达他，他俩强联通。

(4)、假设我们已经dfs完了u的所有的子树那么之后无论我们再怎么dfs，u点的low值已经不会再变了。

那么如果dfn[u]=low[u]这说明了什么呢？

再结合一下dfn和low的定义来看看吧

dfn表示u点被dfs到的时间，low表示u和u所有的子树所能到达的点中dfn最小的。

这说明了u点及u点之下的所有子节点没有边是指向u的祖先的了，即我们之前说的u点与它的子孙节点构成了一个最大的强连通图即强连通分量

此时我们得到了一个强连通分量，把所有的u点以后压入栈中的点和u点一并弹出，将它们的vis置为false，如有需要也可以给它们打上相同标记（同一个数字）

对了，tarjan一遍不能搜完所有的点，因为存在孤立点或者其他

所以我们要对一趟跑下来还没有被访问到的点继续跑tarjan

怎么知道这个点有没有被访问呢？

看看它的dfn是否为0！

这看起来似乎是o(\(n^2\))的复杂度，但其实均摊下来每个点只会被遍历一遍

所以tarjan的复杂度为o(\(n\))。

tarjan到此结束

参考博文:https://www.cnblogs.com/stxy-ferryman/p/7779347.html