ccf 201803-4 棋局评估(Python实现)

一、原题

问题描述

试题编号：	201803-4
试题名称：	棋局评估
时间限制：	1.0s
内存限制：	256.0MB
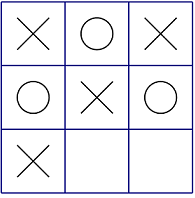
问题描述：	问题描述 　　Alice和Bob正在玩井字棋游戏。 　　井字棋游戏的规则很简单：两人轮流往3*3的棋盘中放棋子，Alice放的是“X”，Bob放的是“O”，Alice执先。当同一种棋子占据一行、一列或一条对角线的三个格子时，游戏结束，该种棋子的持有者获胜。当棋盘被填满的时候，游戏结束，双方平手。 　　Alice设计了一种对棋局评分的方法： 　　- 对于Alice已经获胜的局面，评估得分为(棋盘上的空格子数+1)； 　　- 对于Bob已经获胜的局面，评估得分为 -(棋盘上的空格子数+1)； 　　- 对于平局的局面，评估得分为0； 　　例如上图中的局面，Alice已经获胜，同时棋盘上有2个空格，所以局面得分为2+1=3。 　　由于Alice并不喜欢计算，所以他请教擅长编程的你，如果两人都以最优策略行棋，那么当前局面的最终得分会是多少？ 输入格式 　　输入的第一行包含一个正整数T，表示数据的组数。 　　每组数据输入有3行，每行有3个整数，用空格分隔，分别表示棋盘每个格子的状态。0表示格子为空，1表示格子中为“X”，2表示格子中为“O”。保证不会出现其他状态。 　　保证输入的局面合法。(即保证输入的局面可以通过行棋到达，且保证没有双方同时获胜的情况) 　　保证输入的局面轮到Alice行棋。 输出格式 　　对于每组数据，输出一行一个整数，表示当前局面的得分。 样例输入 3 1 2 1 2 1 2 0 0 0 2 1 1 0 2 1 0 0 2 0 0 0 0 0 0 0 0 0 样例输出 3 -4 0 样例说明 　　第一组数据： 　　Alice将棋子放在左下角(或右下角)后，可以到达问题描述中的局面，得分为3。 　　3为Alice行棋后能到达的局面中得分的最大值。 　　第二组数据： 　　Bob已经获胜(如图)，此局面得分为-(3+1)=-4。 　　第三组数据： 　　井字棋中若双方都采用最优策略，游戏平局，最终得分为0。 数据规模和约定 　　对于所有评测用例，1 ≤ T ≤ 5。

二、题解

三、代码

• 以下提交15分：

num = int(input())
content = []
for i in range(num * 3):
    content.append(list(map(int, input().split())))

def get_li(li):
    i = 0
    narray = []
    for i in range(num):
        narray.append([])
        j = i * 3
        for j in range(j, j + 3):
            narray[i].append(li[j])
    return narray

def judge(li, u=1):
    for i in range(3):
        if li[i][0] == li[i][1] == li[i][2] == u:
            return True
    for i in range(3):
        if li[0][i] == li[1][i] == li[2][i] == u:
            return True
    if li[0][0] == li[1][1] == li[2][2] == u:
        return True
    if li[2][0] == li[1][1] == li[0][1] == u:
        return True
    return False

def space(li, u=0):
    count = 0
    for i in range(3):
        for j in range(3):
            if li[i][j] == u:
                count += 1
    return count

def dfs(li, u):
    max1, min1 = -10, 10
    if (space(li)) >= 7: return 0
    if u == 1 and judge(li, 2):
        return -space(li) - 1
    if u == 2 and judge(li, 1):
        return space(li) + 1
    if (space(li) == 0): return 0

    for i in range(3):
        for j in range(3):
            if li[i][j] == 0:
                li[i][j] = u
                if u == 1:
                    max1 = max(max1, dfs(li, 2))
                else:
                    min1 = min(min1, dfs(li, 1))
                li[i][j] = 0
    if u == 1:
        return max1
    else:
        return min1

for i in get_li(content):
    print(dfs(i, 1))

以下提交：