AGC006

AtCoder Grand Contest 006

<br >

心血来潮，开了一套AGC.....

然后发现各种不会做.........感觉智商被AGC摁在地上摩擦......

<br >

代码戳这里

<br >

A - Prefix and Suffix

这道题目还是送温暖的...

直接枚举长度从\(n\)到\(n+n\)

最后的\(n\)为用第二个字符串填充，剩余空缺从前到后一次用第一个字符串填充

最后验证前\(n\)位是否满足第一个字符串即可

由于是从小到大枚举，枚举到可行直接输出答案即可

---

B - Median Pyramid Easy

这道题目就比较有意思了

首先考虑不可行的情况，显然当\(x=1\)或\(2*n-1\)的时候是不可行的

因为每一次取的都是三个格子中的中位数，显然到第二行的时候，\(1\)或\(2*n-1\)就消失不见了，更高的行中不可能出现

然后考虑其余情况的构造方法

一种比较通用的构造方法是，最高行为\(x\)，我们使得下一行出现至少两个\(x\)即可，如下图所示

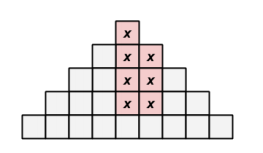
我们只要保证图中所有的红色格子都是\(x\)的话，最后一行一定是\(x\)

那么，现在，我们只需要构造最后一行的四个格子，使得从第二行开始就在指定位置出现连续的两个\(x\)了

这样就比较思博了，\((x-1),(x),(x+1),(x-2)\)即可

但是我们发现，当\(x=2\)的时候，会有点问题，那么我们对\(x=2\)特判一下，构造\((x+1),(x),(x-1),(x+2)\)

当然，构造的方法不唯一

最后注意特判\(n=2\)的情况，不过我这样构造的话，不会出现问题

---

C - Rabbit Exercise

这道期望题目一颗赛艇啊

首先考虑对称位置的处理，显然\(x_i\)关于\(x_{i-1}\)和\(x_{i+1}\)的对称位置分别是\(2*x_{i-1}-x_{i}\)和\(2*x_{i+1}-x_{i}\)

考虑兔子\(i\)的期望

\[E(x_i')=\frac{1}{2}E(2x_{i-1}-x_i)+\frac{1}{2}E(2x_{i+1}-x_i)\]

\[=E(x_{i-1})+E(x_{i+1})-E(x_i)\]

这样，我们似乎已经得到了\(O(MK)\)的算法

我们从几何角度来考虑一下这个操作

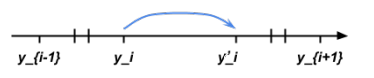
其实就是\(y_i\)相对于\(y_{i-1}\)和\(y_{i-2}\)的相对位置发生了变化，\(y_i\)在外面的情况也是如此

再一般的来说，就是\(E(x_i)-E(x_{x-1})\)和\(E(x_i)-E(x_{x+1})\)的值进行了交换

那么，我们考虑差分，这样，每一次的操作就是对两个数进行交换了

而交换操作是分组进行的，我们可以根据类似快速幂的方式，在\(O(logk)\)的时间内完成交换

那么总的复杂度就是\(O(nlogk)\)

---

D - Median Pyramid Hard

这道题目似乎是B题的SPJ啊.....

考虑二分答案，假设当前需要验证的答案为\(x\)，表示答案\(≥x\)是否成立

那么，根据最下面一行和\(≥x\)的关系，我们可以得到底层的\(0/1\)数列，\(1\)表示\(≥x\)

我们现在得到了底层的\(0/1\)数列，而题目所给的条件，上一层的一格为\(1\)，当且仅当下一层与之对应的三个中至少有两个\(1\)

现在，符合情况的话，那么就是顶层为\(1\)

我们可以画画图来分析一下底层的情况，如何向上传导

我们可以发现，当出现连续的两个\(1\)的时候，他们所对应的的上面，全部为\(1\)

那么，这样的情况如何向外拓展呢？

我们发现，当连续的两个\(1\)旁边出现隔着一个位置的\(1\)的是否，这个全是\(1\)的竖行，可以向着隔着一个位置的\(1\)的方向拓展一列

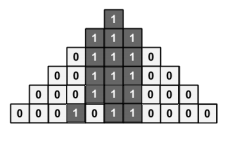
那么我们只需要正着反着，各扫一遍

这样一来，我们就可以在\(O(2n)\)的时间内验证答案了

还有一种比较特殊的情况是，底层不需要出现连续的两个\(1\)

特判一下

总的时间复杂度是\(O(3n*logn)\)

---

E - Rotate 3x3

这道题目很繁琐啊QAQ......

画了满满一页草稿纸......

首先，我们透过现象看本质，3*3Rotate 实际上就是把左右两列交换，然后在把三列全部倒置

那么，其实可以发现，每一列中的三个数是不会改变的，而且三个数要么正向，要么逆向

再其次，因为交换的是间隔的两列，所以矩阵中的奇数列和偶数列其实是相对独立的

我们把操作分成两个来思考

对间隔的两列旋转(这个旋转操作自带一个倒置和一个左右交换)、对某一列倒置

对于第一个问题的数量，我们可以转为这个问题：给出\(n\)个数的一个全排列，每次可以交换相邻的两个数，求每个数被交换的次数

贪心的做，我们先把在最后的数换下去，然后在换倒数第二个.......

暴力的做是\(O(n^2)\)，考虑用树状数组维护一波，\(O(nlogn)\)

第二个问题，只要判断第一个问题的奇偶性，就可以直接得到答案了

那么回到原问题，可行性怎么判断

首先判断前面提到的一些条件...balabala

然后，就是对后面两个子问题的判断了

对于奇数列的第一个问题，左右交换的前提是其中间的偶数列进行倒置

那么，也就是说，奇数列的第一个问题的奇偶性应当与偶数列的第二个问题相同；偶数列的判断亦是如此

这样一来，问题就解决了，时间复杂度\(O(nlogn)\)，不过题解里给出的复杂度是\(O(n)\)，不是很明白他是怎么实现的，可能他的\(d\)数组可以线性求吧Orz

---

F - Blackout

又一次深刻体会到了出题人的强大Orz...

首先，我们可以把这个矩阵问题转变为图论问题

我们把格子\((x,y)\)转变为一条有向边\(x\rightarrow y\)，那么，当\(x\rightarrow y\)和\(y\rightarrow z\)存在时，有边\(z\rightarrow x\)

我们可以先来尝试探索一些规律

对于图中的\(n\)个点，每个点\(x\)都有边连向\(x+1\)，我们尝试更新一波边，发现只有在\(x\)和\(y\)满足\(x+1\equiv y (mod\; 3)\)的时候，\(x\)有指向\(y\)的边

以此，我们发现这张图和\(3\)有关系（出题人是这么说的.......）

于是，我们用三色来对图进行染色，使得相邻的节点不同色

接下来，我们分别讨论三种情况

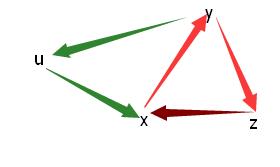
【1】 染色成功，且图中出现了不同的三种颜色\(x\)、\(y\)、\(z\)

那么，我们对于三种不同颜色的边，可以把所有\(x\rightarrow y\)、\(y\rightarrow z\)、\(z\rightarrow x\)都连上

证明:如下图，如果上述情况成立的话，那么，一定至少存在\(x\rightarrow y\)、\(y\rightarrow z\)，我们当然可以把\(z\rightarrow x\)连上，当有新的边\(u\rightarrow x\)时，我们发现，\(y\rightarrow u\)也同样可以连上，那么，联通的所有点都是可以两先关的

【2】染色成功，图中出现的颜色不足三种

那么显然，不存在\(x\rightarrow y\)、\(y\rightarrow z\)这样的边对，那么，答案就是边数

【3】染色失败

那么，画画图很容易看出，一定存在着环（且环的大小一定不是\(3\)的倍数）

那么，很显然得，所有联通的点之间，两两之间的所有边均可以连上

这样一来，我们对于每一个联通块一次这样讨论即可，时间复杂度\(O(m)\)

---

新成就get，打穿了一道AGC