Leetcode 558.四叉树交集

四叉树交集

四叉树是一种树数据，其中每个结点恰好有四个子结点：topLeft、topRight、bottomLeft 和 bottomRight。四叉树通常被用来划分一个二维空间，递归地将其细分为四个象限或区域。

我们希望在四叉树中存储 True/False 信息。四叉树用来表示 N * N 的布尔网格。对于每个结点, 它将被等分成四个孩子结点直到这个区域内的值都是相同的。每个节点都有另外两个布尔属性：isLeaf 和 isLeaf。当这个节点是一个叶子结点时 isLeaf 为真。val 变量储存叶子结点所代表的区域的值。

例如，下面是两个四叉树 A 和 B：

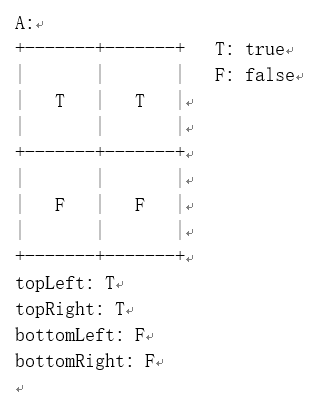
你的任务是实现一个函数，该函数根据两个四叉树返回表示这两个四叉树的逻辑或(或并)的四叉树。

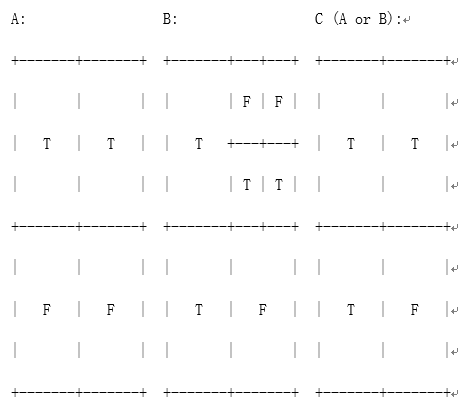
提示：

1. A 和 B 都表示大小为 N * N 的网格。
2. N 将确保是 2 的整次幂。
3. 如果你想了解更多关于四叉树的知识，你可以参考这个 wiki 页面。
4. 逻辑或的定义如下：如果 A 为 True ，或者 B 为 True ，或者 A 和 B 都为 True，则 "A 或 B" 为 True。

 /*
 // Definition for a QuadTree node.
 class Node {
     public boolean val;
     public boolean isLeaf;
     public Node topLeft;
     public Node topRight;
     public Node bottomLeft;
     public Node bottomRight;

     public Node() {}

     public Node(boolean _val,boolean _isLeaf,Node _topLeft,Node _topRight,Node _bottomLeft,Node _bottomRight) {
         val = _val;
         isLeaf = _isLeaf;
         topLeft = _topLeft;
         topRight = _topRight;
         bottomLeft = _bottomLeft;
         bottomRight = _bottomRight;
     }
 };
 */
 class Solution {
     public Node intersect(Node quadTree1, Node quadTree2) {
         if(quadTree1 == null || quadTree2 == null) {
             return null;
         }
         if(quadTree1.isLeaf && quadTree2.isLeaf) {
             return new Node(quadTree1.val || quadTree2.val, true, null, null, null, null);
         }
         else if(quadTree1.isLeaf) {
             return quadTree1.val ? new Node(quadTree1.val, true, null, null, null, null)
                     : new Node(quadTree2.val, quadTree2.isLeaf, quadTree2.topLeft, quadTree2.topRight, quadTree2.bottomLeft, quadTree2.bottomRight);
         }
         else if(quadTree2.isLeaf) {
             return quadTree2.val ? new Node(quadTree2.val, true, null, null, null, null)
                     : new Node(quadTree1.val, quadTree1.isLeaf, quadTree1.topLeft, quadTree1.topRight, quadTree1.bottomLeft, quadTree1.bottomRight);
         }

         Node topLeft = intersect(quadTree1.topLeft, quadTree2.topLeft);
         Node topRight = intersect(quadTree1.topRight, quadTree2.topRight);
         Node bottomLeft = intersect(quadTree1.bottomLeft, quadTree2.bottomLeft);
         Node bottomRight = intersect(quadTree1.bottomRight, quadTree2.bottomRight);

         Node root = new Node();
         if(topLeft.isLeaf && topRight.isLeaf && bottomLeft.isLeaf && bottomRight.isLeaf &&
                 topLeft.val == topRight.val && topRight.val == bottomLeft.val && bottomLeft.val == bottomRight.val) {
             root.val = topLeft.val;
             root.isLeaf = true;
         }
         else {
             root.isLeaf = false;
             root.topLeft = topLeft;
             root.topRight = topRight;
             root.bottomLeft = bottomLeft;
             root.bottomRight = bottomRight;
         }
         return root;
     }
 }