关于利用STL栈求解四则中缀表达式以及中缀表达式转逆波兰表达式和逆波兰表达式的求解

今天总结一下栈的一个重要应用---四则数学表达式的求解

数学表达式的求解是栈的一个重要的应用，在计算机的应用中

如果求解一个四则运算表达式，我们可能会直接写一个程序例如什么printf("%d",a+b)这些类似的简单代码实现加减乘除运算

但如果给你一个这样的表达式：9+(3-1)*3+10/2，这样的表达式对于计算机的困难点是乘除号出现在了加减号的后面，并且加上括号就更加麻烦了，

而只识别01的计算机可能会只按照式子从左往右挨个计算，这就忽略了四则运算表达式的按顺序计算，因此，我们需要设计一种算法来实现对于这类四则运算表达式的求解

我们都知道，对于有左括号的式子一定会有右括号但是有右括号的式子却不一档有左括号，因此我们需要一种储存的数据结构来实现逆序存储和匹配，因此就用了栈这种数据结构；

遇到左括号就进站，出现右括号左括号出战并且让数字参与运算；

但是很遗憾的是，括号也是四则运算式的一部分，有没有一种方法可以让括号不出现在运算式中呢？

答案是有的：

有一种表达式被称为是逆波兰表达式的表达式可以避免括号的出现，这种表达式不需要括号出现，并且是一种后缀表达式

后缀之地方在于运算符是出现在运算数之后的

例如这样的表达式

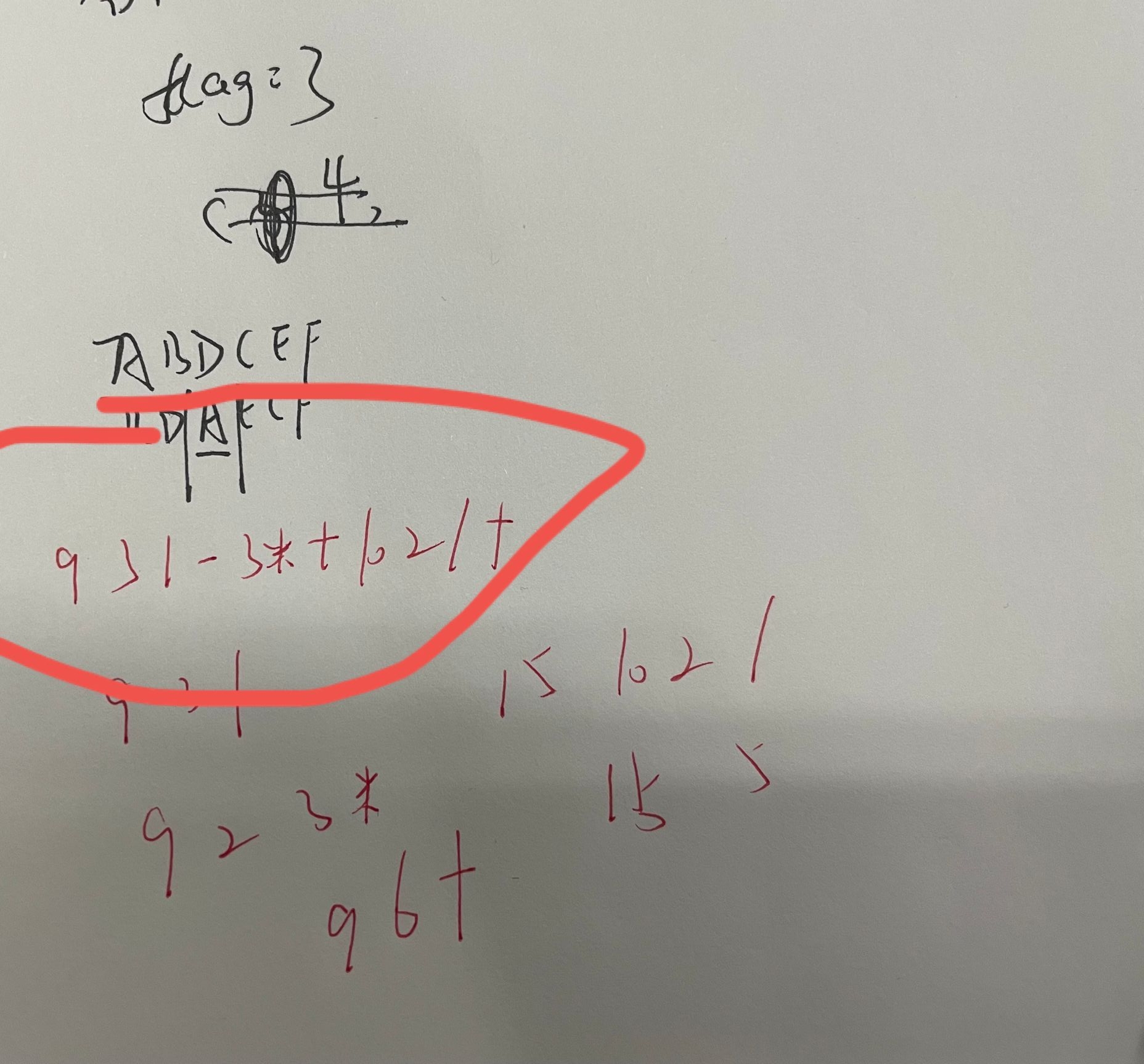
像这样，就避免了括号的出现，使运算更加简单；

那怎么将中缀表达式转成逆波兰表达式呢？

转换的标准是酱紫的：

碰到数字就输出，如果是运算符先判断与栈顶符号的优先级，是右括号或者优先级小于等于栈顶符号的，将栈顶元素一次输出并且弹栈，并且把当前符号进栈，直到输出后缀表达式；

当然这样说显得很笼统，我总结了一下记忆的方式：

按照这样的法则就可以将中缀表达式转成逆波兰表达式啦；

来举个栗子：9+(3-1)*3+10/2

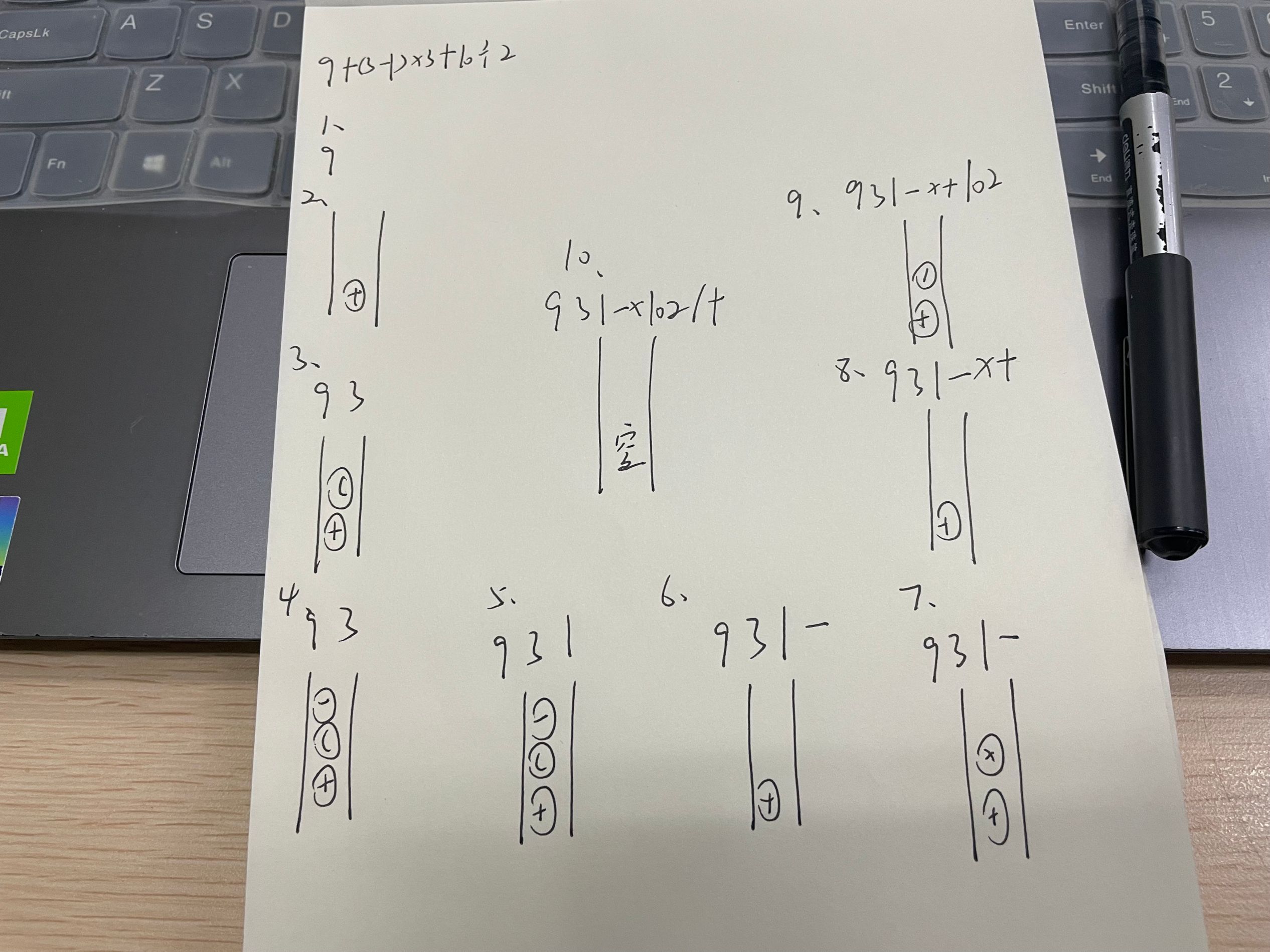
转化方式和步骤是酱紫的，

我们接下来用代码实现一下：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 stack<char>q;
 4 string s;
 5 int main()
 6 {
 7     std::ios::sync_with_stdio(false);
 8     cin.tie(0);
 9     cout.tie(0);
10     getline(cin,s);
11     for(register int i=0;i<s.size();i++)
12     {
13         if(s[i]>='a'&&s[i]<='z')//碰到数字直接输出
14         cout<<s[i];
15         else if(s[i]==')')//如果碰到右括号，就找到左括号与它相匹配
16         {
17             while(true)
18             {
19                 if(q.top()=='(')//碰到了就弹栈并且停止
20                 {
21                     q.pop();
22                     break;
23                 }
24                 cout<<q.top();
25                 q.pop();//没找到之前一直弹栈并输出
26             }
27         }
28         else//运算符
29         {
30             if(!q.empty()&&(s[i]=='+'||s[i]=='-')&&(q.top()=='*'||q.top()=='/'))//碰到加号或者减号
31             {
32                 while(!q.empty())
33                 {
34                     if(q.top()=='(')//碰到括号就停止
35                     break;
36                     cout<<q.top();//一直弹栈并输出
37                     q.pop();
38                 }
39                 q.push(s[i]);//当前的元素入栈
40             }
41             else
42             q.push(s[i]);//其余的入栈
43         }
44     }
45         while(!q.empty())
46         {
47             cout<<q.top();
48             q.pop();
49         }
50     return 0;
51 }

逆波兰表达式转化成功了，怎么求逆波兰表达式的值呢：

很简单，从头开始扫描，如果碰到数字就进站，

如果碰到运算符，将栈顶的两个数字出站进行运算，在将结果入栈，一直得到最终的结果；

图解演示一下吧：

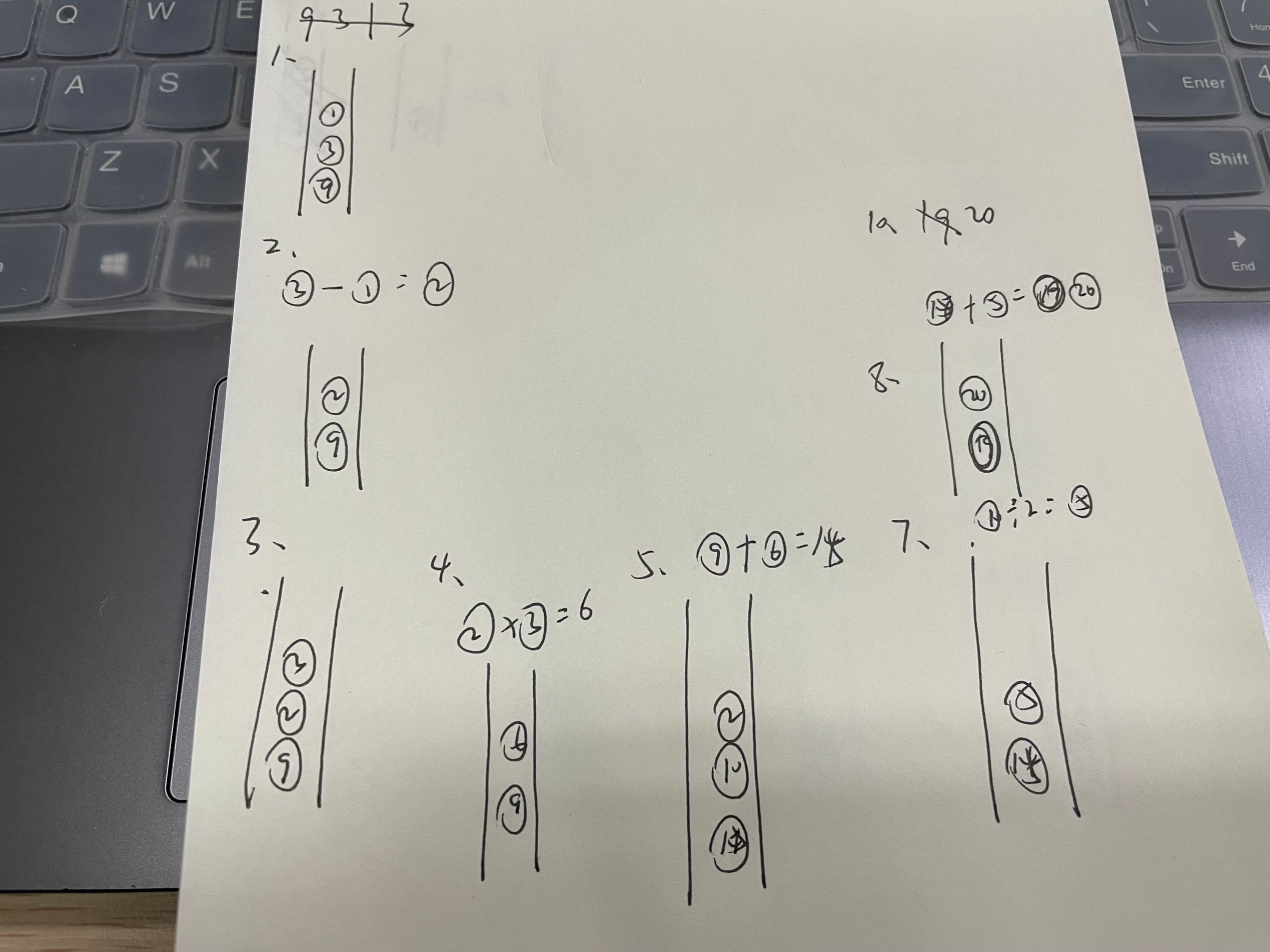
相应的用代码实现是灰常简单的:

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int num=1e4+10;
 4 char ch[num];
 5 int n;
 6 stack<int>q;
 7 bool operatorpoland(char op)//判段是不是运算符
 8 {
 9     if(op=='+'||op=='-'||op=='*'||op=='/')
10     return true;
11     else
12     return false;
13 }
14 int reversepoland()
15 {
16     int a,b;
17     for(register int i=0;i<n;i++)
18     {
19         if(!operatorpoland(ch[i]))//如果不是运算符
20         {
21             q.push((ch[i]-'0'));//入栈
22         }
23         else
24         {
25             int a=q.top();//取栈顶两个元素进行运算
26             q.pop();
27             int b=q.top();
28             q.pop();
29             if(ch[i]=='+')//如果运算符是加号
30             q.push(a+b);
31             else if(ch[i]=='-')//如果运算符号是减号
32             q.push(a-b);
33             else if(ch[i]=='*')//乘号
34             q.push(a*b);
35             else if(ch[i]=='/')//除号
36             q.push(a/b);
37         }
38     }
39     return q.top();//最后得到栈顶的元素即是结果
40 }
41 int main()
42 {
43     std::ios::sync_with_stdio(false);
44     cin>>ch;
45     n=strlen(ch);
46     printf("%d",reversepoland());
47     return 0;
48 }

可以拿两道题目练练手：

https://acm.sdut.edu.cn/onlinejudge3/contests/3980/problems/F

http://acm.hdu.edu.cn/showproblem.php?pid=1237（水却处理起来有些麻烦）

一会会看情况把没学完的kmp算法给补上；

那就先到这里啦~~~~