AlphaTensor论文阅读分析

目前只是大概了解了AlphaTensor的思路和效果，完善ing

deepmind博客在 https://www.deepmind.com/blog/discovering-novel-algorithms-with-alphatensor

论文是 https://www.nature.com/articles/s41586-022-05172-4

解决"如何快速计算矩阵乘法"的问题

问题建模

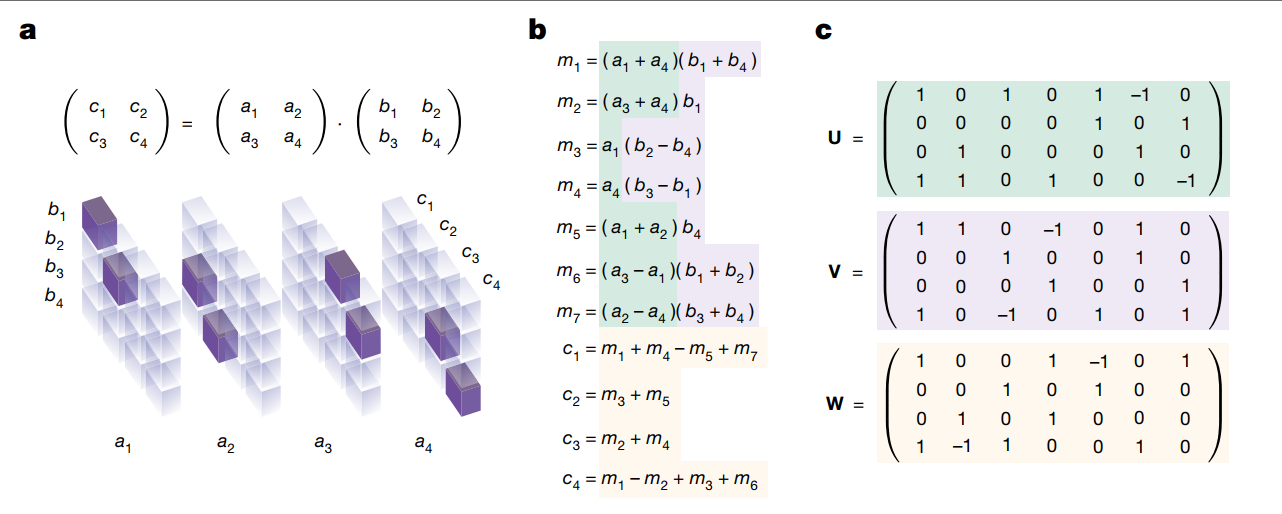
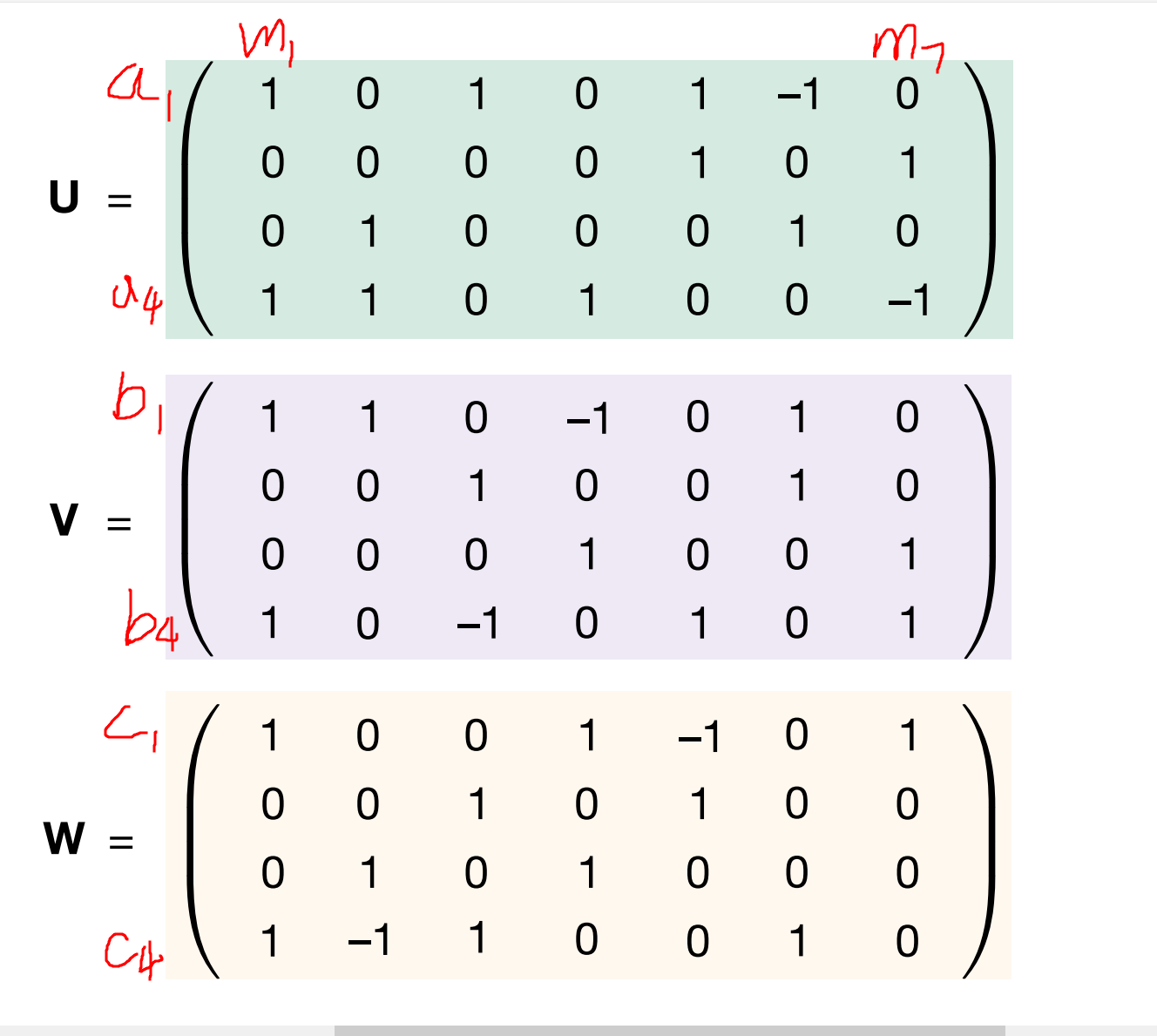
变成single-player game

\[\tau_n= \sum_{r=1}^R \textbf{u}^{(r)} \otimes \textbf{v}^{(r)} \otimes \textbf{w}^{(r)}
\]

In $2*2*2$ case of Strassen, R is 7. (see the fig.c). The goal of DRL algorithm is to minimize R (i.e. total step)

the size of $\textbf{u}^{(r)} $ is $(n^2, R)$.

$ \textbf{u}^{(1)}$ is the first column of u: $(1,0,0,1)^T$

$ \textbf{v}^{(1)}$ is the first column of v: $(1,0,0,1)^T$

$\textbf{u}^{(1)} \otimes \textbf{v}^{(1)} = $

\[\begin{bmatrix} 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\1 & 0 & 0 & 1 \end{bmatrix}\quad
\]

上面矩阵的第一行代表a1，第四行代表a4，第一列代表b1... (1,1)位置出现一个1，表示当前矩阵代表的式子里面有个$a_1b_1$ ，上面这个矩阵对应的是m1=(a1+a4)(b1+b4)

$\textbf{u}^{(1)} \otimes \textbf{v}^{(1)} \otimes \textbf{w}^{(1)} $ 就是再结合上ci，哪些ci中包括m1这一项。最终三者外积得到的是$n*n*n$的张量，ci对应的$n*n$矩阵内记录的就是ci需要哪些ab的乘积项来组合出来。当然，最终需要R个这样的三维张量才能达到正确的矩阵乘法。

(第一步是选择mi如何由ai bi组成，这对应上面那个$n*n$的矩阵。第二步是选择ci如何由mi组成，这对应着$\textbf{w}$那个$(n^2, R)$的矩阵。两步合在一起得到R个$n*n*n$的三维张量，R个三维张量加起来得到$\tau_n$，$\tau_n$中挑出ci那一维，对应的矩阵就是ci如何由ai bi组成)。

按照朴素矩阵乘法，$c_1=a_1*b_1+a_2*b_3$ ，因此，无论采用什么路径，合计出来的三维张量$\tau_n$，在c1这个维度上都必须是

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}\quad
\]

因此，可以用朴素矩阵乘法算出最终的目标，即$\tau_n$ 。

step

在step 0, $S_0=\tau_n$. (target)

在游戏的step t, player选择一个三元组 $(u^{(t)}, v^{(t)}, w^{(t)})$ : $S_t \leftarrow S_{t-1} - \textbf{u}^{(t)} \otimes \textbf{v}^{(t)} \otimes \textbf{w}^{(t)} $

目标是用最少的步数达到zero tensor $S_t=\vec 0$

所以 action space 是 $\{0,1\}^{n^2} \times \{0,1\}^{n^2} \times \{0,1\}^{n^2}$

为了避免游戏被拉得太长: $R \le R_{limit}$ ( $R_{limit}$ 步之后终止)

reward:

每一个step: -1 reward （为了找到最短路）

如果在non-zero tensor终止: $-\gamma(S_{R_{limit}})$ reward

($\gamma(S_{R_{limit}})$ 是terminal tensor的rank的上界)

constrain $\{u^{(t)}, v^{(t)}, w^{(t)}\}$ in a user-specified discrete set of coeffients F

AlphaTensor

有些类似于 AlphaZero

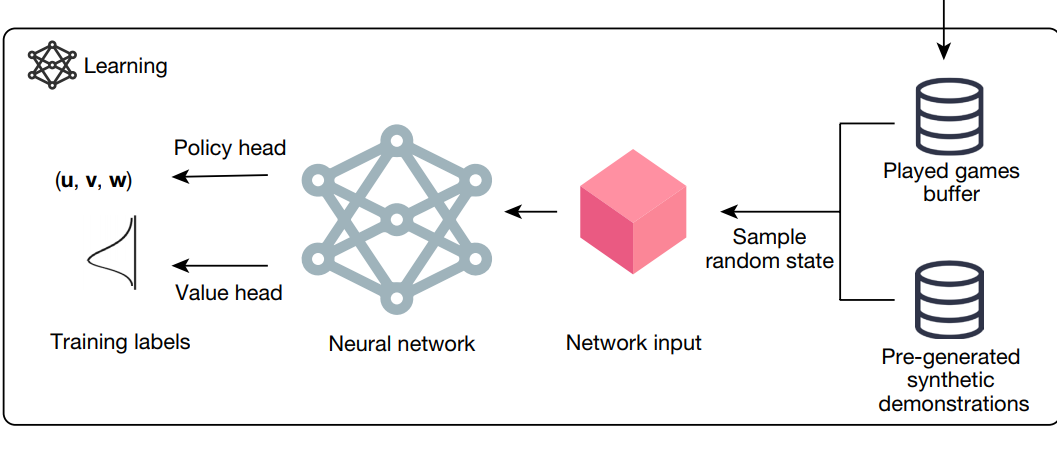
一个deep nn 去指导 MCTS.
state作为输入, policy (action上的一个概率分布) 和 value作为输出

算出最优策略下每一步的action: $\{(u^{(r)}, v^{(r)}, w^{(r)})\}^R_{r=1}$ 之后，就可以拿uvw用于矩阵乘法了

效果

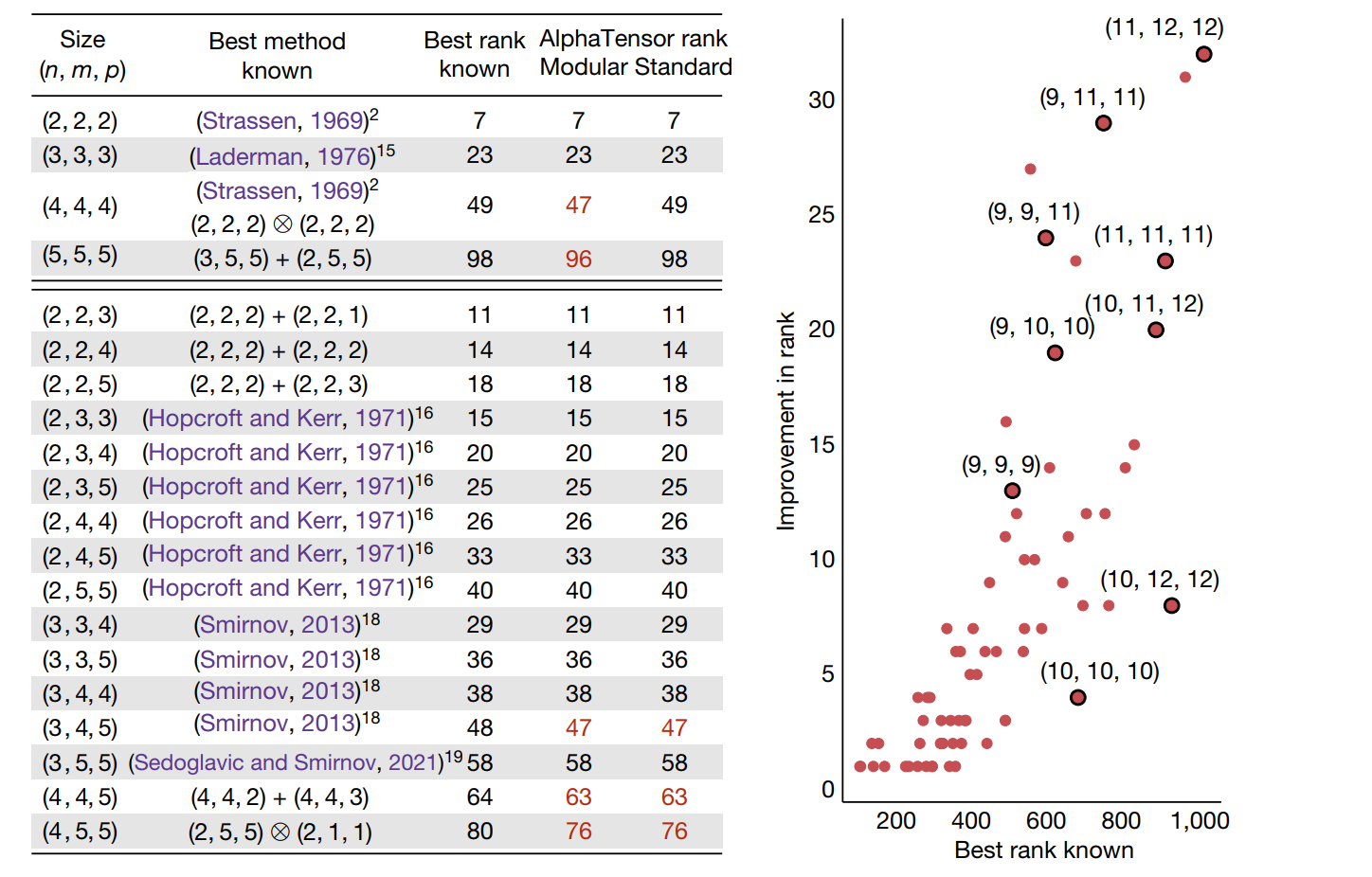
可以看到，AlphaTensor搜索出来的计算方法，在部分矩阵规模上达到了更优的结果，即乘法次数更少。

在第四行，(5,5,5)情形下的矩阵乘法，AlphaTensor计算出来的方法可以在博客里面看到，非常复杂，为了减少两次乘法，却耗费了数几十次加法。因此AlphaTensor只能做到渐进时间复杂度更优，在大矩阵情形下达到更快的速度。

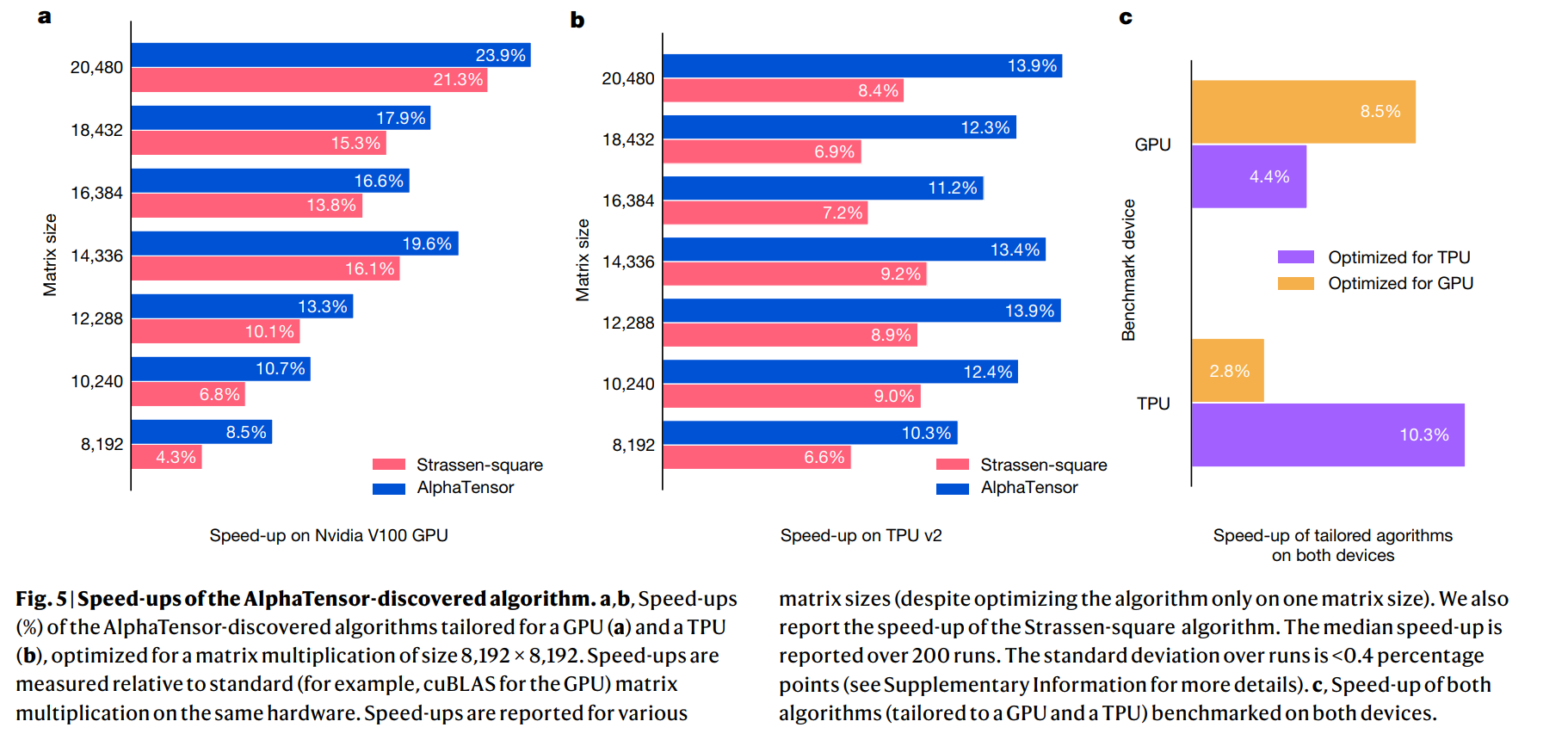
值得关注的是，他们在$8192*8192$的方阵乘法上进行了测试，采用$4*4$分块的方式（这样每个子矩阵的大小就是$2048*2048$规模的了），AlphaTensor方法比Strassen的方法减少了两次矩阵乘法，因此加速比从1.043提升至1.085。这说明这一方法相比coppersmith-winograd方法($O(n^{2.37})$)那种银河算法更加实用，常数更低，在8192规模的矩阵就能生效了。而且，计算矩阵乘法的Algorithm 1也方便在GPU和TPU上并行。