P1030

题面

给出一棵二叉树的中序排列与后序排列。求出它的先序排列。（约定树结点用不同的大写字母表示，长度≤8）。

输入格式

2行，均为大写字母组成的字符串，表示一棵二叉树的中序排列与后序排列。

输出格式

1行，表示一棵二叉树的先序排列。

样例

输入

BADC

BDCA

输出

ABCD

前置知识

先序遍历

若二叉树为空，则空操作，否则：

访问根结点、先序遍历左子树、先序遍历右子树

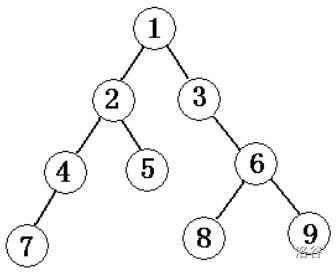
先序遍历此图结果为：124753689

中序遍历

若二叉树为空，则空操作，否则：

中序遍历左子树、访问根结点、中序遍历右子树

中序遍历上图结果为：742513869

后序遍历

若二叉树为空，则空操作，否则：

后序遍历左子树、后序遍历右子树、访问根结点

后序遍历上图结果为：745289631

思路分析

我们可以发现，一棵树后序排列的最后一位就是这棵树树的根节点。以样例为例，后序排列BDCA中最后一位为A，因此这棵树的根节点为A。

我们又可以发现，在一棵树的中序排列中，这棵树的根节点将它的中序排列分为两部分，即此根节点的左子树和它的右子树。同样以样例为例，中序排列BADC被根节点分为两部分，即B和DC两棵子树。

那么，我们只需要继续以同样的方法，递归寻找两棵子树的左子树和右子树就可以了。

代码实现中的难点

如何快速确定根节点在中序排列中的位置？

关于这一点我们当然可以一个一个地找过去，但为了让程序跑得更快，我们可以模仿映射的思想，建立一个数组，记录后序排列中的每一位在中序排列中的位置（具体实现看代码）

#include<iostream>
#include<cstring>
#include<cstdio>
#define ll long long
using namespace std;
char mid[10],post[10];
//mid数组记录中序排列，post数组记录后序排列
//除了打暴力最好不要用string
int z[10],m[10],p[10];
//z数组做中转使用，m数组记录mid数组的内容，p数组记录post数组的每一位在mid数组中的位置
void find(int start,int end,int kai,int jie){
//start和end记录我们正在找的mid数组的范围
//kai（开头）和jie（结尾）记录我们正在找的post数组的范围
    if(start>end||kai>jie)return;
    //如果开头大于结尾，就返回
    if(start==end||kai==jie){
        printf("%c",mid[p[jie]]);
        return;
    }
    //如果开头等于结尾，那此节点一定没有儿子，输出当前节点并返回
    printf("%c",mid[p[jie]]);
    //前面说过后序排列的最后一位就是当前树的根节点，所以p[jie]就是根节点在mid数组中的位置
    //开头小于结尾，那就输出当前节点然后再去寻找此节点的左儿子和右儿子
    find(start,p[jie]-1,kai,kai+p[jie]-start-1);
    //求左子树的范围，然后递归寻找左儿子
    find(p[jie]+1,end,kai+p[jie]-start,jie-1);
    //求右子树的范围，然后递归寻找右儿子
}
int main(){
    scanf("%s%s",mid+1,post+1);
    //输入时下标从1开始（主要是因为我比较毛病）
    int len=strlen(mid+1);
    //输入时下标从1开始那么计算字符串长度时也要加1
    for(int i=1;i<=len;i++){
        m[i]=mid[i]-'A'+1;
        //将每一位转成数字以方便处理（是的，我很毛病）
        z[m[i]]=i;
        //z数组记录m数组每一位的位置（这一步是为了方便后面记录post数字）
    }
    for(int i=1;i<=len;i++){
        p[i]=z[post[i]-'A'+1];
        //记录post数组的每一位在mid数组中的位置
        //z：我滴任务完成啦！
    }
    find(1,len,1,len);
    //开始递归
    return 0;
}

如此就完成啦~