【Linear Support Vector Machine】林轩田机器学习技法

首先从介绍了Large_margin Separating Hyperplane的概念。

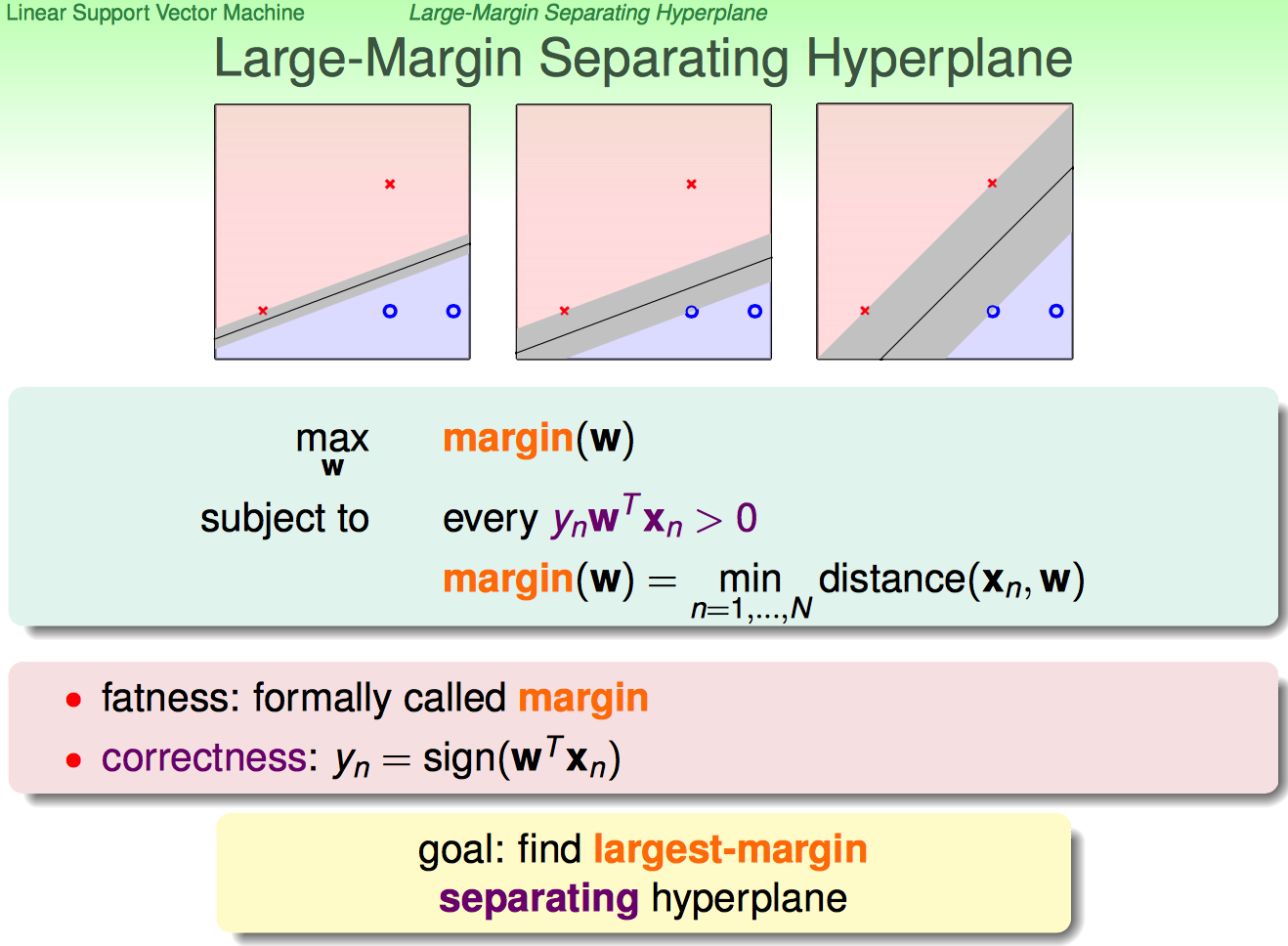
（在linear separable的前提下）找到largest-margin的分界面，即最胖的那条分界线。下面开始一步步说怎么找到largest-margin separating hyperplane。

接下来，林特意强调了变量表示符号的变化，原来的W0换成了b（这样的表示利于推导；觉得这种强调非常负责任，利于学生听懂，要不然符号换来换去的，谁知道你说的是啥）

既然目标是找larger-margin separable hyperplane，那就得先弄明白一个点到平面的距离是啥。

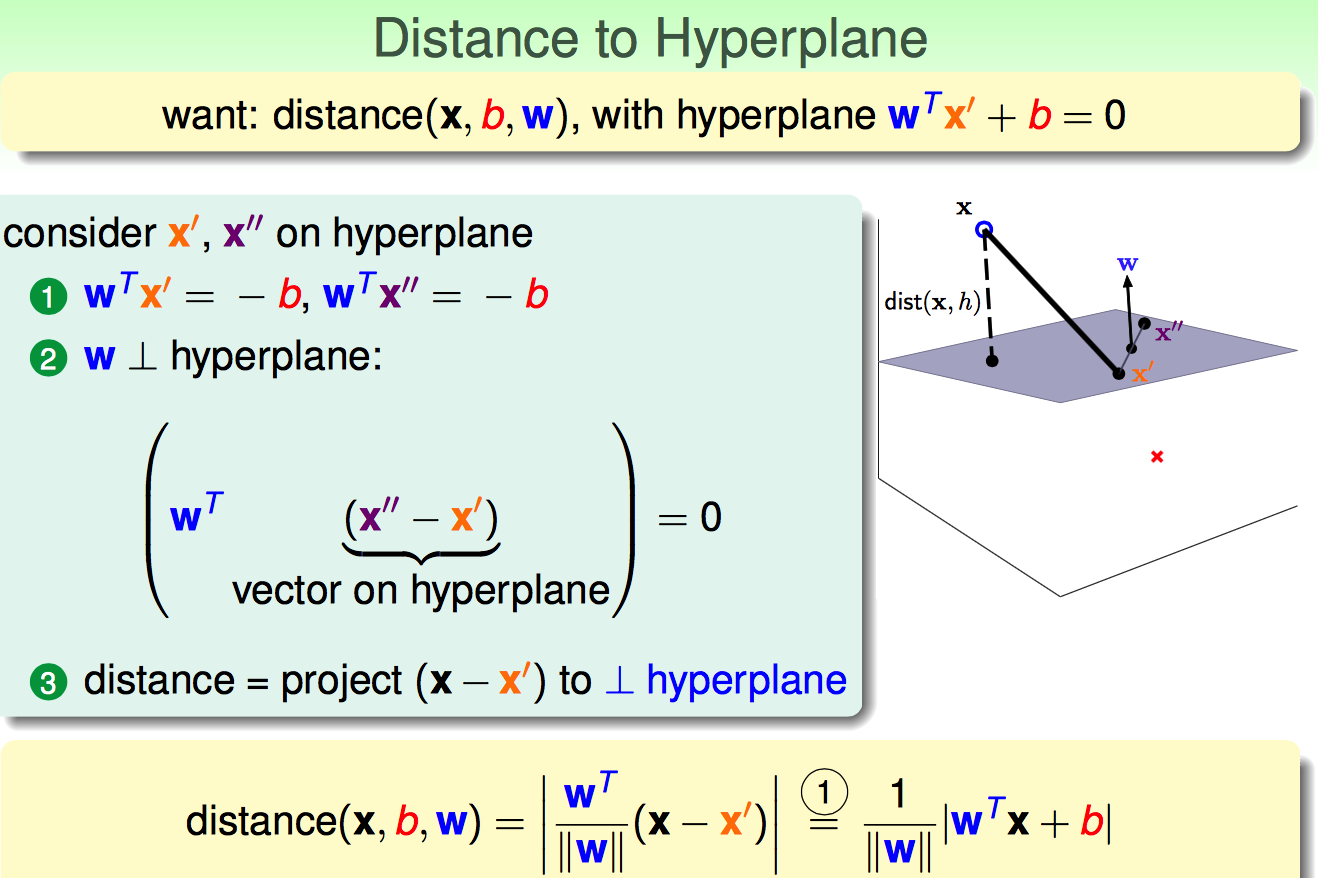
假设x'是平面上的点，x是平面外的点；那么x到平面的距离可以用x-x'再投影到平面法向量w上。

有了点到hyperplane的表达式，就可以把我们需要的larger-margin条件的分类面的求解条件表示出来。

由于假设是数据是linear separable的，所以有yn(W'xn+b)>0。

这时候看subject to部分：

（1）every那条保证了求出的超平面一定是可以分开的

（2）margin那条包含两个意思：

　　a. 啥叫margin啊？就是离hyperplane最近的点到hyperplane的距离；每个给定的满足条件的hyperplane，都对应一个margin(b,W)

　　b. 也就是说：一个（b, W）就对应一个hyperplane → 如果hyperplane满足yn(W'xn+b)>0（n=1,...,N）→ 则对应一个margin(b,W)

这样连起来看就捋清晰了：对于某一个separable hyperplane，求margin(b,W)是一个求min的过程；对于所有separable hyperplane产生的margins，求所有margins里面最大的那个margin是一个求max的过程。

截至到上面，larger-margin separable hyperplane的问题就列清楚了。下面开始，就是如何不断简化上约束条件和求解目标。

这里直接从margin的表达式入手，强行指定min yn(W'xn+b)=1 (n=1,...,N)；这样margin的表达式就变成了1/||W||这个形式。

我看过的一些资料，对这个的解释就是：对（b,W）放缩大小，使得margin上的点yn(W'xn+b)=1。

上面的说法比较直观，从几何角度规定了这样一个简化方法；但是这种一笔带过的解释并不能使我完全信服，下面从公式的角度解释一下为什么可以做上面的替换。

　　对于某个hyperplane(b,W)来说，margin是min (1/||W||) * (yn(W'xn+b))，如果直接让yn(W'xn+b)=1，凭什么说1/||W||还是margin呢？

可以这样想：

　　（1）假设对于某个hyperplane(b,W)来说，margin的值是v（确定的值）→

　　（2）min (1/||W||) * (yn(W'xn+b)) = v (n=1,...,N) →

　　（3）min 1/ (||W||/s) * (yn(W'xn/s+b/s)) = v (n=1,...,N) →

　　（4）令yn(W'xn/s+b/s) = 1 ，再令Wnew = W/s , bnew = b/s →

　　（5）则有 min (1/||Wnew||) * (yn(Wnew'xn+bnew)) = v (n=1,...,N) →

　　（6）1/||Wnew|| = v

==================================================

2015-09-09

至于为什么可以放缩w'xn+b，可以从几何角度来理解。以两维输入特征为例：

超平面的方程是：

（1）x1+x2+1：w=[1, 1]' , b=1

（2）10x1+10x2+10：w=[10,10]', b=10

看这两个方程，虽然w和b都不同，但是其实是同一条线。

（1）法向量方向相同，大小不同

（2）直线到（0，0）点的距离都是1/sqrt(2)

==================================================

通过以上6个步骤，令min yn(W’xn+b)=1的背后道理明确了。再进一步简化约束条件，如下：

上面用了一个反证法说明这种替代是可行的。

另外，还有一点需要强点：这里之所以敢把最优化目标函数设定为1/2W'W正是因为，只有当yn(W‘xn+b)=1的时候才能取到最优化的结果。

接下来，用一个例子引出了Support Vector的概念。

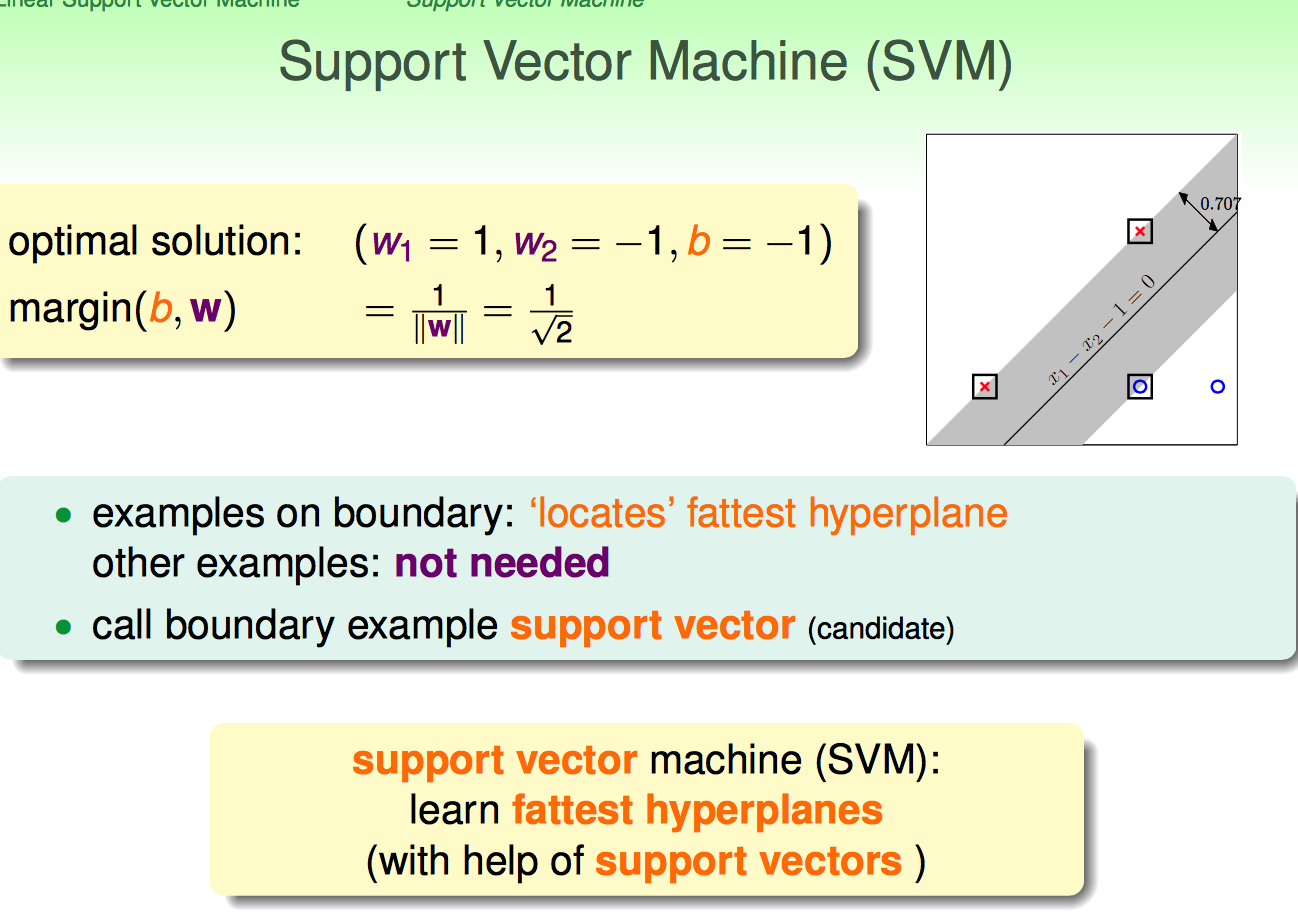
用于hyperplane的这些vector称为support vector。

下面的内容，让我耳目一新。

到上面，突然没有乱七八糟的事情了；林直接说，这是一个典型的quadratic programming（QP）问题；

典型的特点：最优化的表达式是二次的；即这种问题是有常规套路去解的。

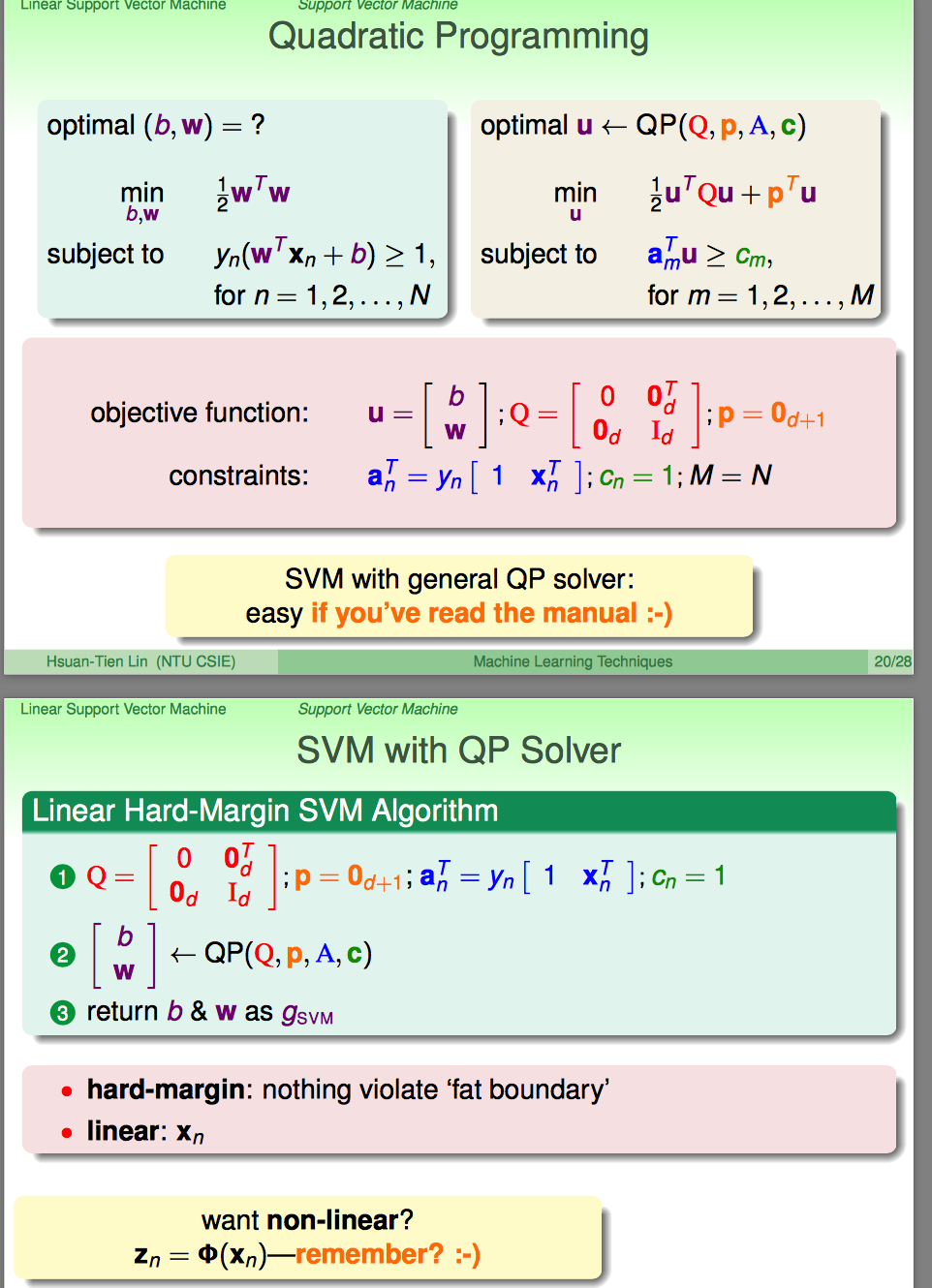
怎么按照QP的常规套路去搞呢？整理出来几个参数就OK了。看到这里，似乎有些傻掉了：说好的KKT那些玩意呢？都不讲了么？

到这里想想也没有啥必要了，都QP直接解出来了，还啥KKT啊。

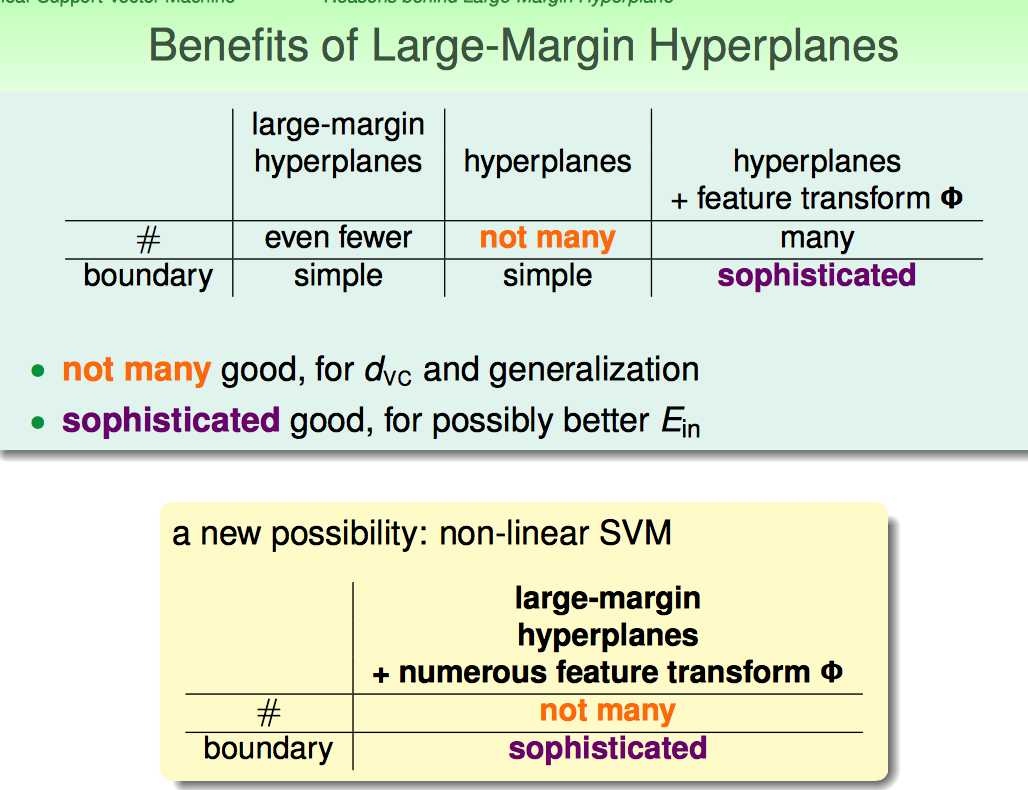
接下来解释了Large-Margin Hyperplane的背后道理。

Large-Margin控制模型复杂度，控制VC维。

简而言之，Large-Margin的好处就是在带入non-linear transform的情况下，可以控制模型的复杂度。