Leetcode 70. Climbing Stairs 爬楼梯 (递归,记忆化，动态规划)

题目描述

要爬N阶楼梯，每次你可以走一阶或者两阶，问到N阶有多少种走法

测试样例

Input: 2
Output:  2

Explanation: 到第二阶有2种走法
1. 1 步 + 1 步
2. 2 步

Input: 3
Output:  3
Explanation:  到第三阶有3种走法
1. 1 步 + 1 步 + 1 步
2. 1 步 + 2 步
3. 2 步 + 1 步

详细分析

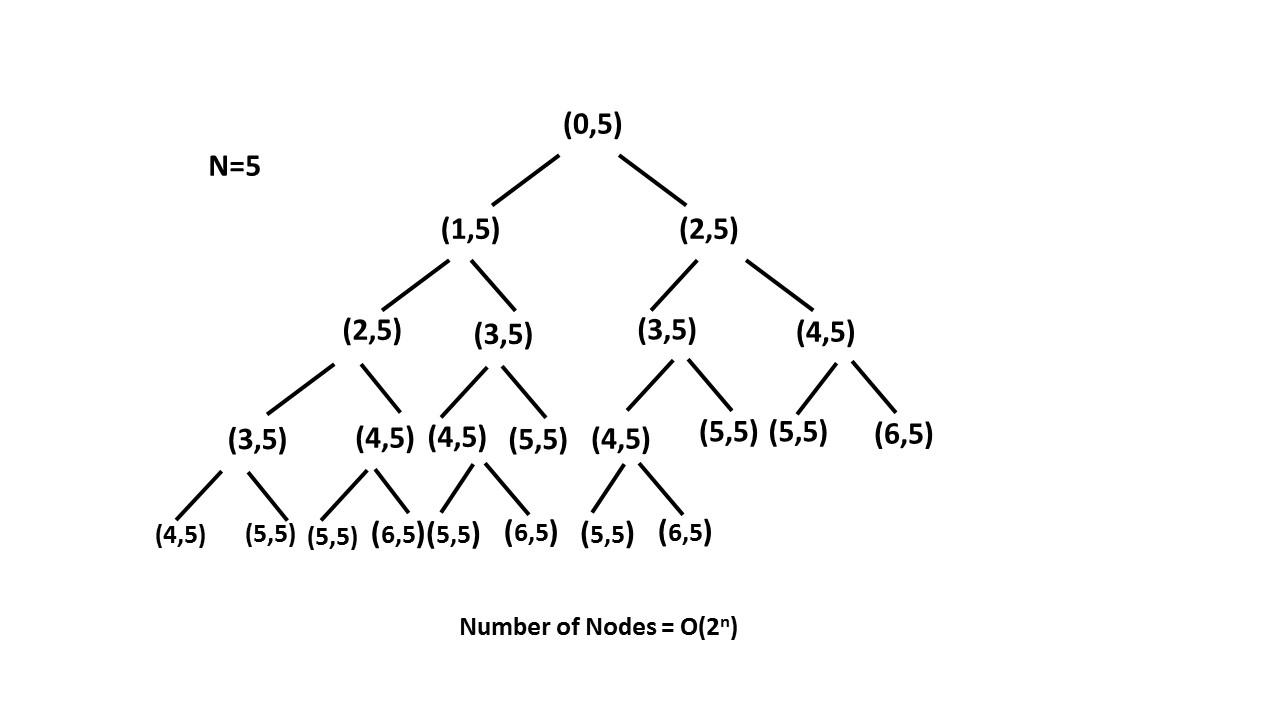
在第0阶，可以选择走到第1阶或者第2阶，第1阶可以走第2阶或者第3阶，第二阶可以走第3阶或者第4阶...。如此继续就生成了上图递归解答树。注意如果直接递归会超时，当前实现使用了记忆化储存子解。

算法实现

记忆化递归(√)

class Solution {
public:
    int climbStairs(int n) {
        this->n = n;

        memo = new int[n+];
        for(int i=;i<n+;i++){
            memo[i] = -;
        }

        return recursiveClimbing();
    }

    int recursiveClimbing(int currentStep){
        if(memo[currentStep]!=-){
            return memo[currentStep];
        }

        if(currentStep==n){
            return ;
        }
        if(currentStep>n){
            return ;
        }
        memo[currentStep] = recursiveClimbing(currentStep+) + recursiveClimbing(currentStep+);
        return memo[currentStep];
    }
private:
    int n;
    int total = ;
    int *memo;
};