《机器学习实战》学习笔记第十四章 —— 利用SVD简化数据

相关博客：

吴恩达机器学习笔记（八） —— 降维与主成分分析法(PCA)

《机器学习实战》学习笔记第十三章 —— 利用PCA来简化数据

奇异值分解(SVD)原理与在降维中的应用

机器学习(29)之奇异值分解SVD原理与应用详解

主要内容：

一.SVD简介

二.U、∑、V^T三个矩阵的求解

三.U、∑、V^T三个矩阵的含义

四.SVD用于PCA降维

五.利用SVD优化推荐系统

六.利用SVD进行数据压缩

一.SVD简介

1.SVD分解能够将任意矩阵着矩阵（m*n）分解成三个矩阵U（m*m）、Σ（m*n）、V^T（n*n），如下：

Data_mxn = U_mxm∑_mxnV^T_nxn

2.Σ是一个对角矩阵，其对角元素是从大到小排列的，它们对应了Data矩阵的奇异值。这些奇异值的含义类似于PCA中特征值的含义。

3.V是一个列矩阵（因而V^T是一个行矩阵）、是一个标准正交基，可用于将数据集Data矩阵进行列降维（即减少列数），其作用类似于PCA中的正交矩阵P。

4.U是一个列矩阵、是一个标准正交基，可用于将数据集Data矩阵进行行降维（即减少行数）。

二.U、∑、V三个矩阵的求解及其含义

可知：D = U∑V^T

则：D^TD = V∑^TU^TU∑V^T = V∑^T∑V^T  = V∑²V^T，因为U为正交矩阵，所以U^TU = I， 因为∑为对角矩阵，所以∑^T∑可表示为∑²。

即：D^TD = V∑²V^T

可知D^TD是一个方阵，方阵即可求出他的特征值和特征向量

(D^TD)X = λX

其中∑²就是特征值λ构成的对角矩阵，V就是特征向量X构成的正交矩阵。

因此，可以用求解特征值和特征向量的方法求解矩阵∑、V。同理，通过求解DD^T的特征值和特征向量可以求解出矩阵U。

三.U、∑、V^T三个矩阵的含义

1.矩阵V的含义：根据上一节，可知矩阵V就是D^TD的特征向量组成的正交矩阵，也就是正交基。而在PCA中，正交基P也是D^TD的特征向量组成的正交矩阵。即，求解矩阵V实际上是在PAC中求解P。而正交基P正是用于对矩阵D进行列降维(减少列数，即减少属性个数)，因此得出结论：矩阵V用于对矩阵D进行列降维。

2.矩阵U的含义：与矩阵V相对，矩阵U用于对矩阵D进行行降维(减少行数，即减少数据点个数)。

3.根据上一节，矩阵∑²就的对角元素就是D^TD的特征值，那么矩阵∑的对角元素D^TD的特征值的开根。∑的对角元素又称为奇异值。注意：求解U和求解V时∑²是不一样的，一个是m*m，一个是n*n，但它们的对角元素是一样的(min(m,n)个奇异值，缺少的用0表示)。

四.SVD用于PCA降维

1.SVD即奇异值分解，可以用来降维。利用PCA降维不挺好的，什么还要用SVD呢？

因为在使用PCA进行降维时，需要计算协方差矩阵X^TX，而如果样本数、特征数都特别多时，计算X^TX将非常耗时。但利用SVD，可以不用求出协方差矩阵X^TX也能得到用于降维的矩阵。实际上，sklearn的PCA就是用SVD求解的。

2.类似于PCA，如果前k个奇异值所对应包含的信息超过了90%，那么可以只利用前k维进行数据压缩，如下：

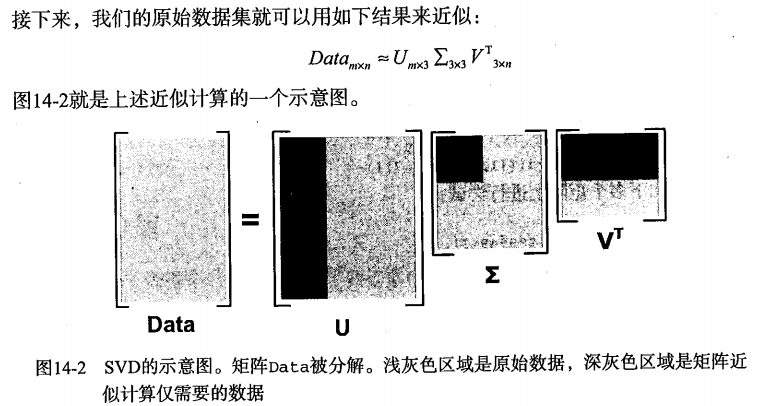
在传输数据时，我们可以只传U（m*k）、Σ（k*k）、V^T（k*n）这三个小矩阵。当接受完数据时，就可以将这三个小矩阵进行矩阵乘法，从而得到原始数据集矩阵Data的近似矩阵。这种方式大大压缩了存储（或传输）的数据量，但又保证了高相似度。

2.SVD可用于降维，将求得的U（m*m）矩阵保留前k列，然后将数据集Data映射的U（m*k）上，实现降维。同理矩阵V（m*m）。

五.利用SVD优化推荐系统

 def ecludSim(inA, inB):     # 计算两数组的相似度
     return 1.0 / (1.0 + la.norm(inA - inB))

 def pearsSim(inA, inB):  # 同上
     if len(inA) < 3: return 1.0
     return 0.5 + 0.5 * corrcoef(inA, inB, rowvar=0)[0][1]

 def cosSim(inA, inB):   # 同上
     num = float(inA.T * inB)
     denom = la.norm(inA) * la.norm(inB)
     return 0.5 + 0.5 * (num / denom)

 '''对单个物品进行预测评分'''
 def standEst(dataMat, user, simMeas, item):
     n = shape(dataMat)[1]       # 物品数
     simTotal = 0.0; ratSimTotal = 0.0     # 总相似度、总评分， 预测频分 = 总评分/总相似度
     for j in range(n):      # 枚举所有物品
         userRating = dataMat[user, j]   # 获取该用户对此物品的评分
         if userRating == 0: continue        # 如果未进行评分，则下一个物品
         overLap = nonzero(logical_and(dataMat[:, item].A > 0, dataMat[:, j].A > 0))[0]  #寻找对两个物品都评了分的用户
         if len(overLap) == 0:   #  计算相似度
             similarity = 0
         else:
             similarity = simMeas(dataMat[overLap, item], dataMat[overLap, j])
         print 'the %d and %d similarity is: %f' % (item, j, similarity)
         simTotal += similarity
         ratSimTotal += similarity * userRating
     if simTotal == 0:
         return 0
     else:
         return ratSimTotal / simTotal

 '''对单个物品进行预测评分，利用SVD对用户进行降维'''
 def svdEst(dataMat, user, simMeas, item):
     n = shape(dataMat)[1]
     simTotal = 0.0; ratSimTotal = 0.0
     U, Sigma, VT = la.svd(dataMat)  # 奇异值分解
     Sig4 = mat(eye(4) * Sigma[:4])  # 取前四个奇异值进行降维
     xformedItems = dataMat.T * U[:, :4] * Sig4.I  # 降维（用户那一栏减少了）
     for j in range(n):
         userRating = dataMat[user, j]
         if userRating == 0 or j == item: continue
         similarity = simMeas(xformedItems[item, :].T, xformedItems[j, :].T)
         print 'the %d and %d similarity is: %f' % (item, j, similarity)
         simTotal += similarity
         ratSimTotal += similarity * userRating
     if simTotal == 0:
         return 0
     else:
         return ratSimTotal / simTotal

 '''推荐算法'''
 def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
     unratedItems = nonzero(dataMat[user, :].A == 0)[1]  # 寻找该用户未评分的物品
     if len(unratedItems) == 0: return 'you rated everything'
     itemScores = []     # 预测评分列表
     for item in unratedItems:   #枚举每一个未评分的物品，进行预测评分
         estimatedScore = estMethod(dataMat, user, simMeas, item)
         itemScores.append((item, estimatedScore))
     return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]   # 对物品按预测评分进行降序排序

六.利用SVD进行数据压缩

 def printMat(inMat, thresh=0.8):      # 输出图案
     for i in range(32):
         for k in range(32):
             if float(inMat[i, k]) > thresh:
                 print 1,
             else:
                 print 0,
         print ''

 '''图片压缩， numSV为压缩后的维度'''
 def imgCompress(numSV=3, thresh=0.8):
     myl = []
     for line in open('0_5.txt').readlines():    # 读取图案
         newRow = []
         for i in range(32):
             newRow.append(int(line[i]))
         myl.append(newRow)
     myMat = mat(myl)
     print "****original matrix******"
     printMat(myMat, thresh)
     U, Sigma, VT = la.svd(myMat)    # 奇异值分解
     SigRecon = mat(zeros((numSV, numSV)))
     for k in range(numSV):  # 选取前numSV个奇异值进行压缩
         SigRecon[k, k] = Sigma[k]
     reconMat = U[:, :numSV] * SigRecon * VT[:numSV, :]      # 压缩后的图案
     print "****reconstructed matrix using %d singular values******" % numSV
     printMat(reconMat, thresh)