量子隐形传态1 Quantum Teleportation

量子隐形传态是量子纠缠的又一个应用。

隐形传态，所谓隐形的意思就是没有物质介质就传递了信息，在经典世界，传递信息要有介质，光、电磁波或者其他的什么，但是在量子的世界里，我可以把信息传递给你，并且不传递任何一个量子比特。

量子不能克隆原理

不能克隆就是说，没有任何一个U操作，可以输入\(|\psi\rangle\) 和 \(|0\rangle\) 然后得到输出 \(|\psi\rangle\) 和 \(|\psi\rangle\) 。

why?

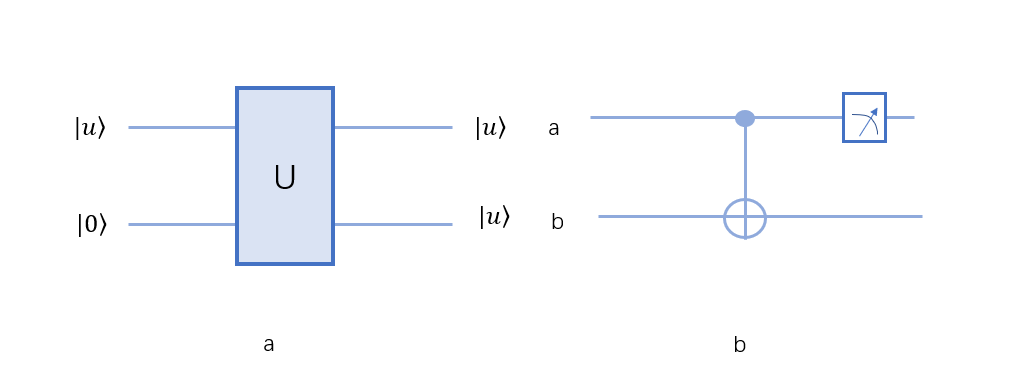
若是真的有这么一个操作算符，如图a，可以复制任意的量子比特 \(|u\rangle\) 我们希望的结果如下：

输入：\((\alpha_0 | 0\rangle +\alpha_1 | 1\rangle)|0\rangle\)

输出：\((\alpha_0 | 0\rangle +\alpha_1 | 1\rangle)(\alpha_0 | 0\rangle +\alpha_1 | 1\rangle)\)

另一方面

我们希望输入是\(|00\rangle\)输出也是\(|00\rangle\)，当输入变成\(|10\rangle\)后，输出也就变成\(|11\rangle\)

而要以上两种情况相等，只有一种可能，即\(|u\rangle\)是\(|0\rangle\)或者\(|1\rangle\)的时候，但是这样，也就没有叠加态的，这样复制的，也就是一个普通的bit。

Teleportation CNOT

那么，如果要把一个自己不知道是什么状态的 \(|u\rangle=\alpha_0 | 0\rangle +\alpha_1 | 1\rangle\) 传递，要怎么办呢？

图b是前面介绍过的CNOT门，有CNOT门，我们很容易就可以把 \(\alpha_0 | 00\rangle +\alpha_1 | 10\rangle\)变成 \(\alpha_0 | 00\rangle +\alpha_1 | 11\rangle\) 。

此时并没有被复制，因为第一个比特和第二个比特之间还是纠缠的，也就是说你测量第一个比特，第二个就会坍缩，你测量第二个，第一个也同理，信息并没有copy两份，所以量子不可复制原理没有被打破。

接下来我们要来处理第一个比特。

如果直接测量第一个比特，很明显，第二个比特就坍缩了。

但是测量还是要测的，不过不是在 \(| 0\rangle\) 、 \(| 1\rangle\) 基，而是在 \(| +\rangle\) 、 \(| -\rangle\) 基。

\[\begin{align}|\psi\rangle&=\alpha_0|00\rangle + \alpha_1|11\rangle\\&=\alpha_0(\frac{1}{\sqrt2}|+\rangle + \frac{1}{\sqrt2}|-\rangle)|0\rangle+\alpha_1(\frac{1}{\sqrt2}|+\rangle - \frac{1}{\sqrt2}|-\rangle)|1\rangle\\&=\frac{1}{\sqrt2}|+\rangle(\alpha_0|0\rangle + \alpha_1|1\rangle)+\frac{1}{\sqrt2}|-\rangle(\alpha_0|0\rangle - \alpha_1|1\rangle) \end{align}\]

在 \(| +\rangle\) 、 \(| -\rangle\) 基对第一个比特测量：
如果测量的结果是 \(|+\rangle\) ，那么第二比特的状态就是 \(\alpha_0 | 0\rangle +\alpha_1 | 1\rangle\) ，正好是我们最初想要传递的态。

如果测量的结果是 \(|-\rangle\) ，那么第二比特的状态就是 \(\alpha_0 | 0\rangle -\alpha_1 | 1\rangle\) ，再经过Z门的翻转就是我们最初想要传递的态了。

参考资料
Quantume Mechanics & Quantume Computation Lecture 5