POJ 1222 EXTENDED LIGHTS OUT（高斯消元解异或方程组）

EXTENDED LIGHTS OUT

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 10835		Accepted: 6929

Description

In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right. 

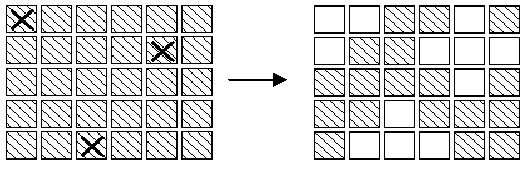
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged. 

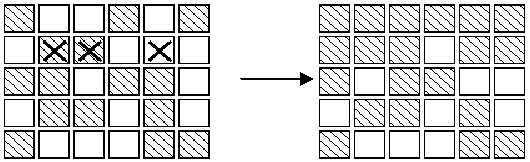
Note: 
1. It does not matter what order the buttons are pressed. 
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once. 
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first 
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off. 
Write a program to solve the puzzle.

Input

The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.

Output

For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.

Sample Input

2
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
0 0 1 0 1 0
1 0 1 0 1 1
0 0 1 0 1 1
1 0 1 1 0 0
0 1 0 1 0 0

Sample Output

PUZZLE #1
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
PUZZLE #2
1 0 0 1 1 1
1 1 0 0 0 0
0 0 0 1 0 0
1 1 0 1 0 1
1 0 1 1 0 1

题目链接：POJ 1222

对于异或方程组的高斯消元感觉用上三角的回代法做比较好，感觉化成行标准型比较麻烦，一共30的方程，首先可以假设第i个方程解第i个未知数，由于开关对自己和周围四个按钮均有影响，那么第$i$个方程的第$i$个变量代表自己，肯定系数为1，设与第$i$个位置相关的其余4个开关标号为$a_i,b_i,c_i,d_i$，那么第$i$个方程显然也与$a_i、b_i、c_i、d_i$有关，即第$i$个方程的第$a_i、b_i、c_i、d_i$位置的系数为1，其余为0（这个很重要，不相关在矩阵里用0代替，而不是不存在），然后化成上三角后用回代法从下至上得到答案。然后由于是模2意义下的加减乘除，可以发现加减法其实就是异或（对于0、1两个数的运算把加减号替换成异或符号不仅结果相同，而且还省去了取模2的麻烦），然后乘法就是做逻辑与即&&运算，除法可以用乘法的逆运算得到，由于当前处理行的要留下的系数肯定为1，然后要消元的行对应的列系数消元之前肯定也是1，因此$系数_1\oplus（*）1 \oplus（-）系数_2\oplus（*）1=系数_1\oplus系数_2$

代码：

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <sstream>
#include <numeric>
#include <cstring>
#include <bitset>
#include <string>
#include <deque>
#include <stack>
#include <cmath>
#include <queue>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
#define fin(name) freopen(name,"ceq",stdin)
#define fout(name) freopen(name,"w",stdout)
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
typedef pair<int, int> pii;
typedef long long LL;
const double PI = acos(-1.0);
const int N = 32;
int Mat[N][N], ans[N];
int id[6][7];

void Gauasian(int neq, int nvar)
{
	int ceq, cvar, i, j;
	for (ceq = 1, cvar = 1; ceq <= neq && cvar <= nvar; ++ceq, ++cvar)
	{
		int teq = ceq;
		for (i = ceq + 1; i <= neq; ++i)
			if (abs(Mat[i][cvar]) > abs(Mat[teq][cvar]))
				teq = i;
		if (teq != ceq)
		{
			for (j = 1; j <= nvar + 1; ++j)
				swap(Mat[ceq][j], Mat[teq][j]);
		}
		for (i = ceq + 1; i <= neq; ++i)
		{
			if (Mat[i][cvar] == 0)
				continue;
			for (j = cvar; j <= nvar + 1; ++j)
				Mat[i][j] ^= Mat[ceq][j];
		}
	}
	for (i = neq; i >= 1; --i)
	{
		ans[i] = Mat[i][nvar + 1];
		for (j = i + 1; j <= nvar; ++j)
			ans[i] ^= (Mat[i][j] && ans[j]);
	}
}
int main(void)
{
	int tcase, i, j;
	scanf("%d", &tcase);
	for (i = 1; i <= 5; ++i)
		for (j = 1; j <= 6; ++j)
			id[i][j] = (i - 1) * 6 + j;
	for (int q = 1; q <= tcase; ++q)
	{
		CLR(Mat, 0);
		CLR(ans, 0);
		for (i = 1; i <= 5; ++i)
			for (j = 1; j <= 6; ++j)
				scanf("%d", &Mat[id[i][j]][31]);
		for (i = 1; i <= 5; ++i)
		{
			for (j = 1; j <= 6; ++j)
			{
				int ID = id[i][j];
				Mat[ID][ID] = 1;
				if (i > 1)
					Mat[ID][id[i - 1][j]] = 1;
				if (i < 5)
					Mat[ID][id[i + 1][j]] = 1;
				if (j > 1)
					Mat[ID][id[i][j - 1]] = 1;
				if (j < 6)
					Mat[ID][id[i][j + 1]] = 1;
			}
		}
		Gauasian(30, 30);
		printf("PUZZLE #%d\n", q);
		for (i = 1; i <= 30; ++i)
			printf("%d%c", ans[i], " \n"[i % 6 == 0]);
	}
	return 0;
}