Qt update刷新之源码分析(二)

大家好，我是IT文艺男，来自一线大厂的一线程序员

上次视频给大家从源码层面剖析了Qt update刷新机制的异步事件投递过程，这次视频主要从源码层面剖析Qt刷新事件(QEvent::UpdateRequest)的处理过程

我们追踪QEvent::UpdateRequest事件处理，进入消息通知流程，即QApplication::notify(QObject *receiver, QEvent *e)函数（没有对QEvent::UpdateRequest事件进行处理），进一步由QApplicationPrivate::notify_helper(QObject *receiver, QEvent * e)函数处理；如下图所示：：

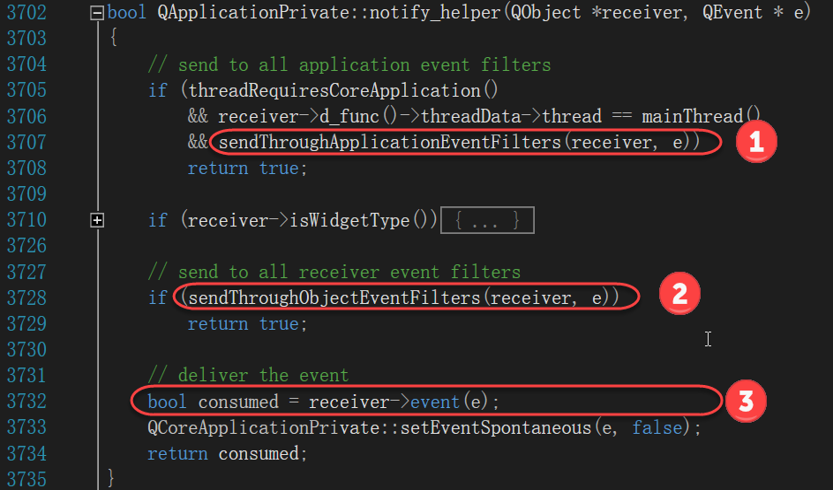
函数主体内容如下：：

1、application的事件过滤器处理，即全局的事件过滤处理

2、receiver的事件过滤器处理，即当前窗口的事件过滤处理

3、调用receiver的event函数处理，即当前窗口的事件处理

receiver的event函数不做处理，如下图所示：：

其调用父类的event函数，即bool QWidget::event(QEvent *event)函数，该函数中针对事件类型进行处理(switch case)，如下图所示：：

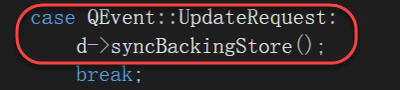
对于QEvent::UpdateRequest事件，则调用syncBackingStore函数，如下图所示：：

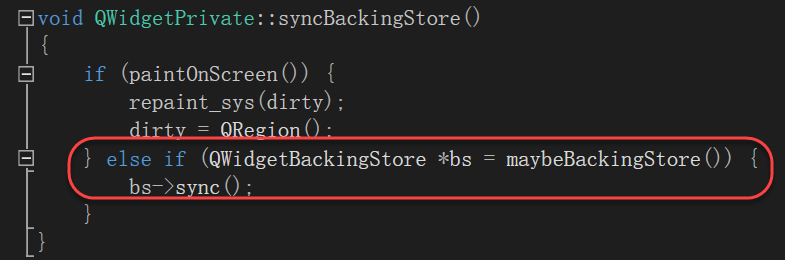
函数主体内容如下：：

1、获取tlw的QWidgetBackingStore

2、调用sync函数

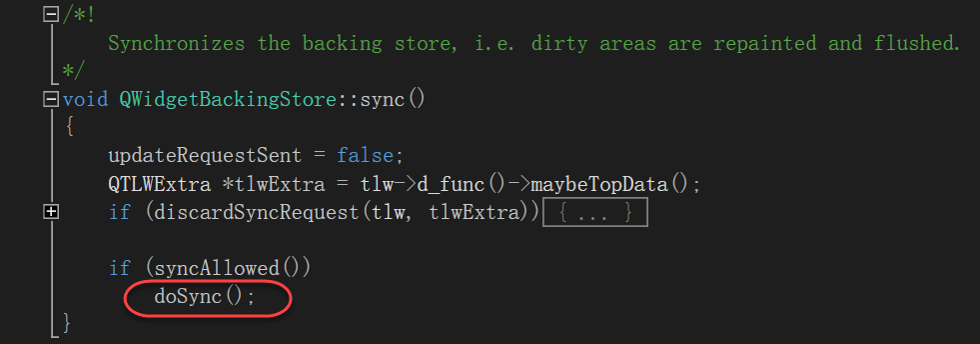
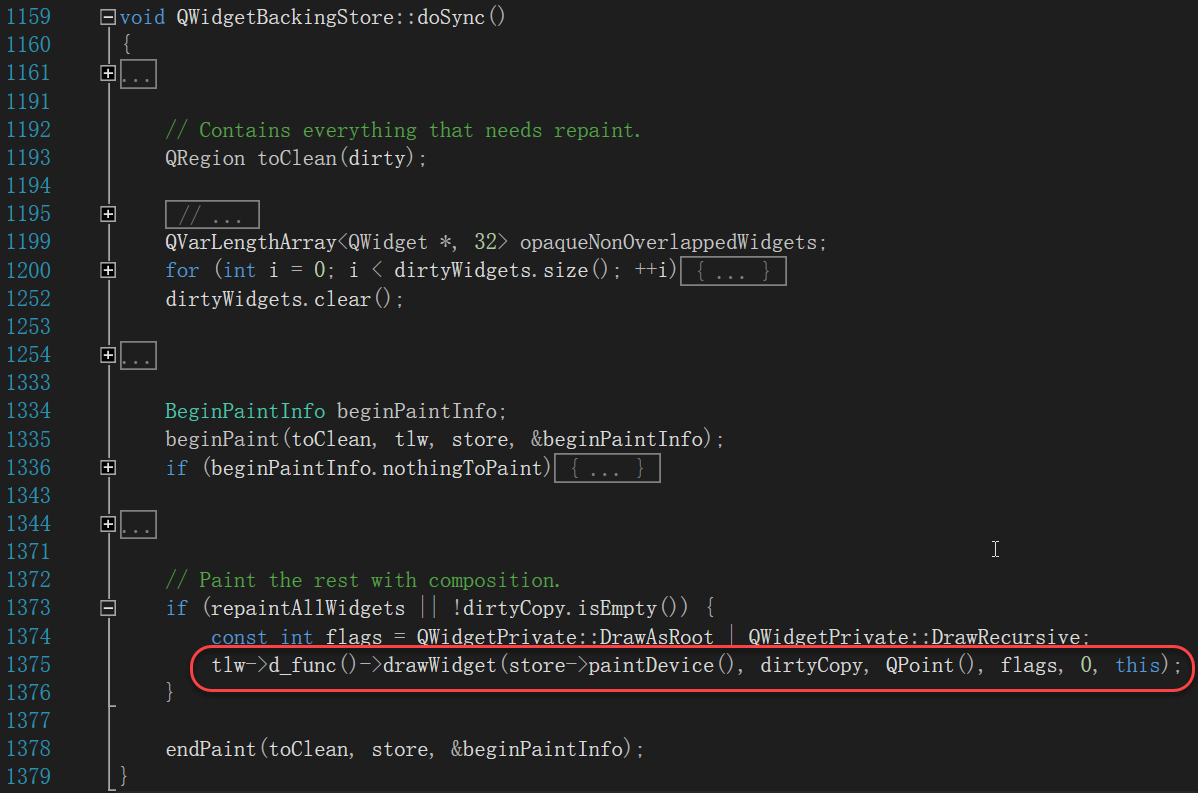
QWidgetBackingStore::doSync函数中调用tlw->d_func()->drawWidget(store->paintDevice(), dirtyCopy, QPoint(), flags, 0, this);函数进行绘制，函数的第一个参数是获取绘制设备，各个平台返回自己的绘制设备，例如对于Windows平台

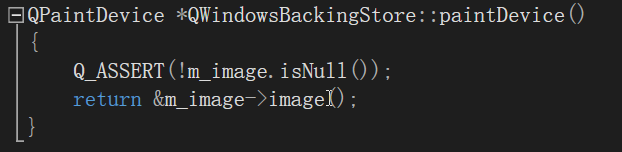
qwindowsbackingstore.cpp文件位于qtbase\src\plugins\platforms\windows目录；

今天就讲解到这里，总结下整体思路即是从事件处理到绘制的过程分析，很清晰;

下次视频进行源码剖析Qt update刷新机制的绘制过程；谢谢