一文读懂GaussDB(for Mongo)的计算存储分离架构

摘要：IDC认为，目前阶段来看，企业亟待解决的是数字化能力提升，包括：与业务的深入结合能力；数据处理和挖掘能力；以及IT技术运营和管理能力。特别是数据处理和挖掘能力，因为数字化转型推进企业从以流程为核心向以数据为核心转型，对海量、异构、多类型的数据处理和挖掘能力是释放数据价值的前提，对数据全生命周期的管控治理是释放数据价值的保障。可以看出，数据库作为数据的承载，企业的要求不再只是简单的存储功能了。

GaussDB(for Mongo)是华为云自主研发兼容MongoDB4.0接口的文档数据库。基于共享存储的存算分离架构，对于传统MongoDB社区版有如下优势：

秒级添加Secondary节点(相比社区版Mongo小时级添加Secondary节点)
基于WAL复制, Secondary节点无写IO,从根本上解决社区版Seconary节点Oplog脱节问题
Primary/Seconary无任何IO交互,Secondary节点个数理论无上限, 支持百万OPS的读事务能力
LSMTree Compaction 计算/IO卸载到Compaction统一调度池,集中管理,不浪费用户读写IO
基于共享存储，Chunk分裂/迁移动作不引起真实IO，只更新路由元数据，秒级分裂/均衡

1.GaussDB(for Mongo)技术架构

1）容忍更多Shard宕机

与社区版MongoDB的`Share-Nothing`模式不同的是，GaussDB(for Mongo)采用`Share-Storage`架构，计算存储分离。集群模式下，N个Shard节点，可以容忍N-1个Shard宕机。

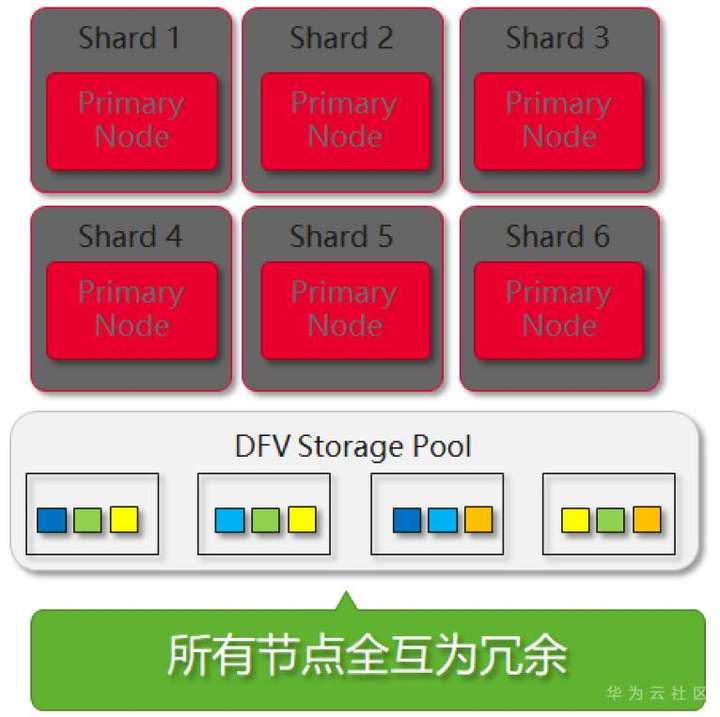
某个Shard节点宕机后，其负责的数据由于存在于共享的存储池中，因此不需要物理拷贝数据，只需要修改元数据路由信息，即可被其他分片节点接管。

2）更快的分裂与均衡能力

此外，由于Chunk数据在存储池中，Chunk的分裂与均衡不涉及到数据拷贝，可以做到分钟级分裂与扩容，分裂与扩容对用户的影响也远比社区版MongoDB小。

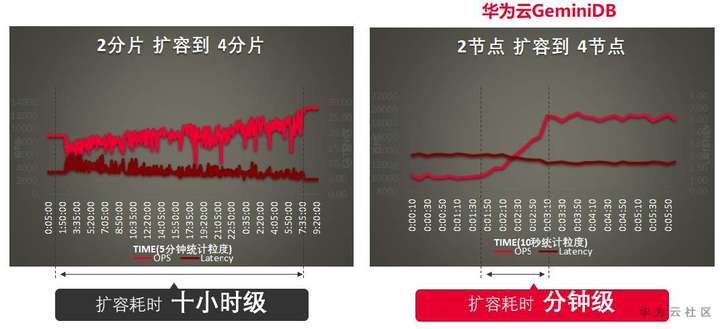
3）百万级读OPS能力

GaussDB(for Mongo)副本集模式下，Primary/Secondary节点之间共享同一份数据库文件。Secondary节点只复制Primary节点的WriteAheadLog以及LSMTree的结构变更信息，并应用到内存中。Secondary节点没有LSMTree的Compaction和Flush任务，因此对用户的读业务影响很小。

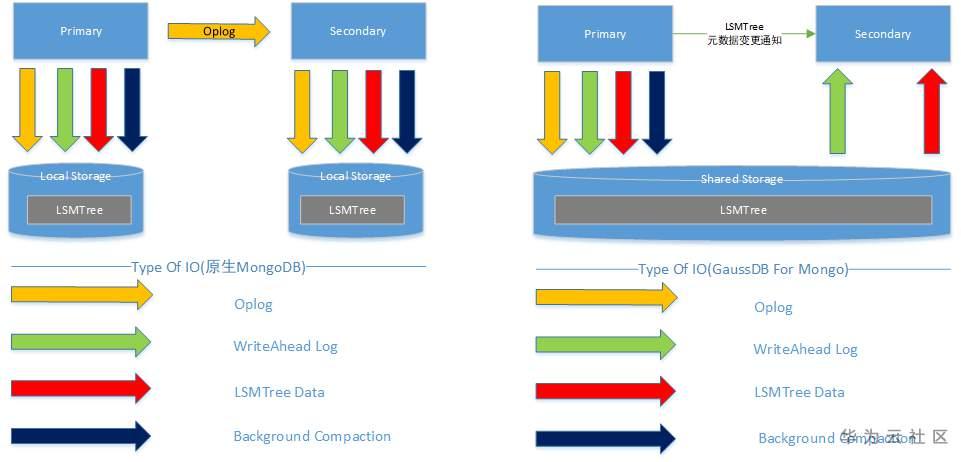
此外，由于`Share-Storage`的架构优势，添加Secondary节点并不需要拷贝数据，添加Secondary节点的动作可以秒级完成。而Primary/Secondary之间只传递元数据变更，不传递WriteAheadLog，因此Secondary节点的个数即使变多，也不影响Primary节点的写性能。Secondary节点可以水平扩展，支撑百万级的读OPS。

4）主节点IO卸载

LSMTree的写压力来源于三部分：

用户的业务写入导致的Memtable Flush
后台SST文件Compaction
WAL的持续写入

根据线上业务的实际测算，三者的IO资源消耗占比为： 1:10:1。后台的SST文件Compaction占了绝大部分IO带宽，通过将Compaction任务集中化管理，从计算池卸载到存储池，进一步减少了用户计算节点的CPU和IO资源消耗。

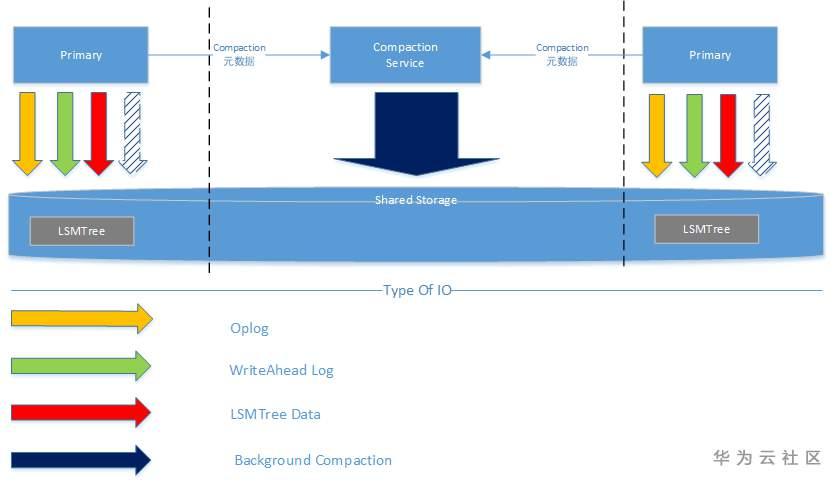
5）GaussDB(for Mongo) 只读节点设计

传统社区版MongoDB副本集基于Oplog做数据复制，只读节点需要镜像主节点的所有写IO操作。GaussDB(for Mongo) 的只读节点和主节点共享同一份底层数据库文件(LSMTree的SST文件)，只读节点并不自己生成SST文件。
随着业务数据的写入，Compaction的不断执行，LSMTree的当前版本(包含哪些SST文件)不断更新，LSMTree的元数据更新(增删SST文件的记录)被同步到只读节点执行。
RocksDB中，数据的变更被持久化到WAL里，元数据的变更(增删文件的操作, 叫做VersionEdit)被持久化到Mainifest里。RocksDB的数据和元数据是分开的，WAL流和VersionEdit流是并行的，没有严格的先后顺序。为了保证只读节点和主节点完全一致的事件回放顺序，WAL和VersionEdit流必须要合并成一个流，在双流合并后，通过LSN就可以为每个事件(WAL的写操作/VersionEdit)定序。

基于WAL+VersionEdit复制，而不基于Oplog复制
共享文件(sst/wal)的生命周期管理由主节点负责sst文件和wal的文件的生命周期由主节点负责。RocksDB中，SST文件通过层级的引用计数来维持不被删除。如下图，RocksDB的每个游标会维持SuperVersion，如下图中的S0，S1，S2。每个SuperVersion会引用一个Version，一个Version代表LSMTree在不断变形(通过增删SST文件变形)的过程中，某个时间点的形状，最新的Version就代表LSMTree当前的形状。

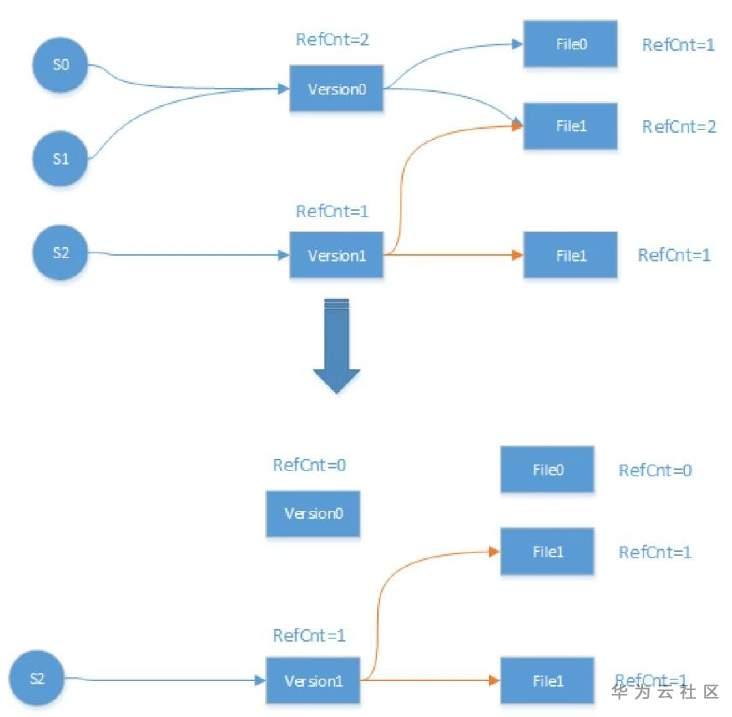
在GaussDB(for Mongo)中，主节点会记录所有只读节点在使用的Version，并为这些Version增加引用计数从而维持SST文件的生命周期。对于WAL，主节点会记录所有只读节点中最老的LSN(`oldestLsn`)，最老的LSN来自于复制最慢的只读节点。并删除比oldestLsn还旧的WAL文件。
元数据变更通知，无论是oldestLsn还是只读节点的当前在用的活跃的Version，都需要及时推进，这些元数据的变更是通过主从节点的定期心跳上报到主节点上的。主节点利用心跳数据对垃圾版本与WAL做清理。如下图所示，在经历一次心跳后，主节点发现Secondary0的Version0和Secondary1的Version0不再使用。删除这两个Version后，SST0的引用计数为0，表示SST0可以被删除。OldestLsn也从100推进到了250，可以清理掉250之前的WAL。

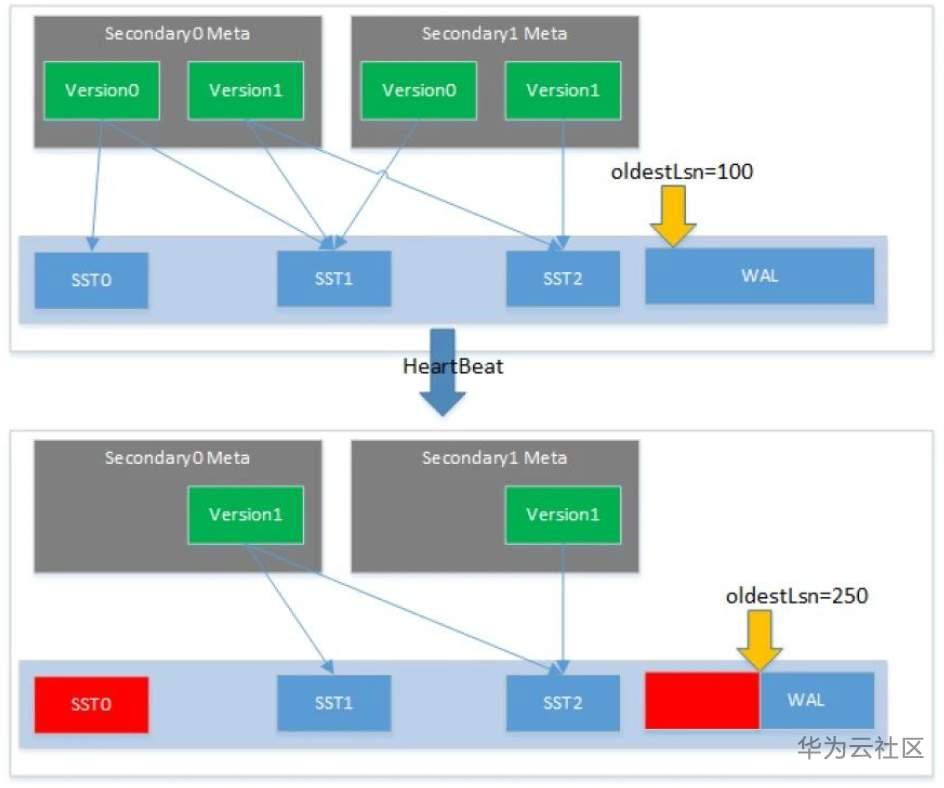
只读节点的memtable的释放：主节点的Memtable不会实时Flush为SST文件。如果只读节点不处理主节点的Memtable的话，只读节点的数据就不是实时的，且存在数据一致性问题。只读节点通过回放WAL到内存的Memtable中，来覆盖SST文件与主节点的Memtable的Gap。上文介绍了只读节点是不往共享存储写入数据的，所以只读节点上的 Memtable 最后的结局一定是被丢弃掉。但什么时候丢弃这个 Memtable 就是一个问题。过早的丢弃，会造成SST文件与Memtable之间的数据不连续，存在Gap，过晚的丢弃会造成内存的浪费。只有当只读节点识别到SST的数据已经完全能够Cover某个Memtable时，这个Memtable才可以被丢弃。
GaussDB(for Mongo)的只读节点在每次应用VersionEdit后，检查所有SST中的最大的LSN与Memtable的最小的LSN的关系，来决定是否要丢弃某个Memtable。
内存元数据的反向更新：传统的复制，数据流从Oplog来，走一遍完整的数据库Server层CRUD接口，再落到引擎层。这种逻辑和主节点上业务的写入逻辑是一致的，因此Server层的一些内存元数据结构，在这个过程中就自然而然的得到更新了。但是当采用基于WAL的复制后，整个WritePath并不经过只读节点的Server层。因此Server层的内存元数据更新，就是一个很大的挑战。在这里，只读节点对每一条WAL做分析，如果WAL的内容会影响Mongo内存元数据，就会reload对应的元数据模块。

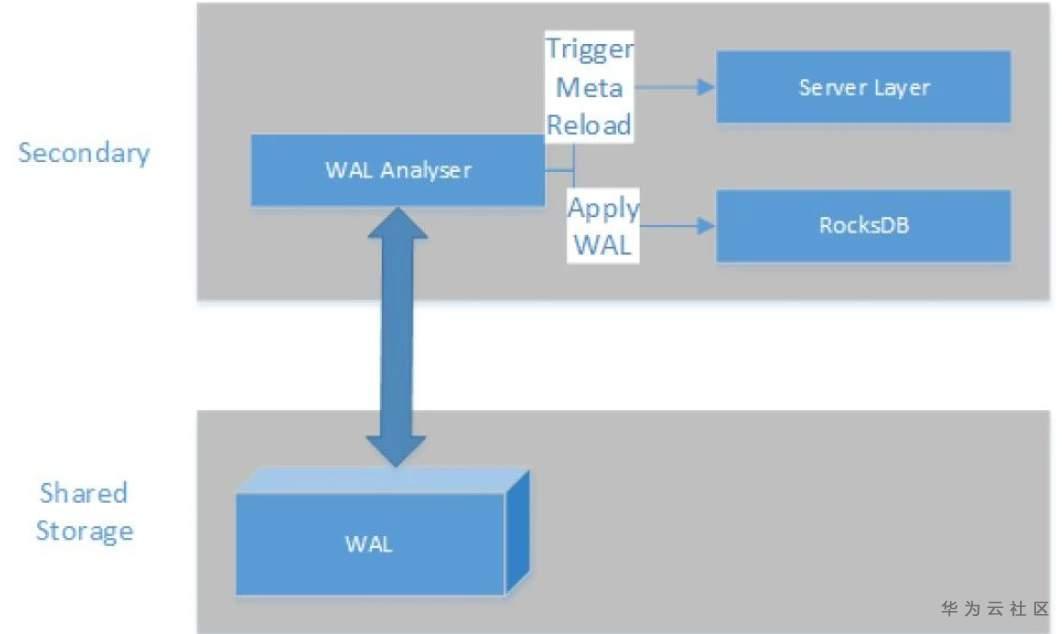
GaussDB(for Mongo) 基于Share-Storage架构，实现秒级Chunk分裂与均衡，对业务影响更小，水平扩展速度更快，能容忍更多节点宕机。只读节点功能，实现了一份数据多计算节点共用的功能。极大的提升了存储的利用效率，提高了计算节点的读取数据能力。为了让副本节点具有持续的读扩展能力，整个只读方案采用元数据的同步模式，在不降低主节点负载的情况下，极大的提升了整个系统的读数据的处理能力。为3节点，5节点，乃至于15节点以上的副本集的工作提供了可能。

数据显示，全球数据量将从2018年32.5ZB快速增长到2025年的180ZB。异构、智能和融合的数据库将成为金融、政府、电信等各行业数据基础设施的关键支柱。华为GaussDB(for Mongo)，能消除企业各业务系统数据孤岛，构建面向行业场景的数据建模、分析和价值挖掘能力，最终帮助企业实现数据价值挖掘和共享。

点击关注，第一时间了解华为云新鲜技术~