[论文阅读笔记] GEMSEC，Graph Embedding with Self Clustering

[论文阅读笔记] GEMSEC: Graph Embedding with Self Clustering

---

本文结构

1. 解决问题
2. 主要贡献
3. 算法原理
4. 参考文献

---

(1) 解决问题

已经有一些工作在使用学习到的节点表示来做社区发现，但是仅仅局限在得到节点表示之后使用聚类算法来得到社区划分，简单说就是节点表示和目标任务分离了，学习到的节点表示并不能很有效地应用于聚类算法（因为可能节点表示向量所在的低维空间中并不存在容易容易划分的簇，从而使用聚类算法也不能得到很好的社区划分结果）。

---

(2) 主要贡献

Contribution 1： 提出GEMSEC，一个基于序列的图表征模型，学习节点表征的同时进行节点的聚类。

Contribution 2： 引入平滑正则项来迫使具有高度重叠邻域的节点对有相似的节点表示。

---

(3) 算法原理

GEMSEC算法主要的框架还是遵循DeepWalk的算法框架，即随机游走生成语料库，再利用简单神经网络来训练节点表示向量。

• 对于随机游走部分，GEMSEC简单采用DeepWalk的一阶随机游走。
• 对于所使用的简单神经网络，原本DeepWalk采用的是以最大化窗口内节点共现概率为目标的Skip-Gram模型，而GEMSEC仅仅在Skip-Gram目标函数（窗口内节点的共现概率）的基础上加上了和聚类有关的目标函数，从而将表示向量学习目标和聚类目标联合在一起优化，得到更加适合聚类（簇的内聚程度高，簇间分明）的表示向量，在学习表示向量的同时也生成了节点的社区划分。

总的目标函数=Skip-Gram目标函数+聚类目标函数，如下所示：

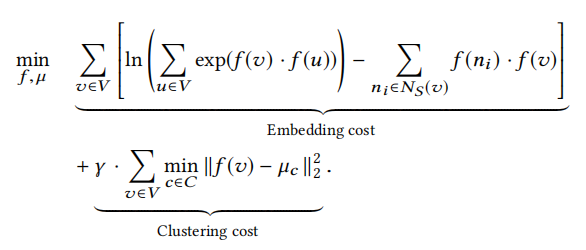
上述目标函数中用到的符号解释如下：

f-the\ mapping\ function\ (from\ node\ to\ embedding\ vector)

f(v)-the\ embedding\ vector\ of node\ v

N_{S}(v)-the\ collection\ of\ windows\ containing\ v

C-the\ set\ of\ communities

u_{c}-the\ vector\ of\ cluster\ center

\gamma-the\ weight\ coefficient\ of\ the\ clustering\ cost

上述目标函数中，第一项（公式中的Embedding cost）为使用了Softmax的节点共现概率函数化简后的形式，主要作用是使得采样的序列中同一个窗口内的节点的表示向量具有相似的表示。第二项（公式中的Clustering cost）为聚类的目标函数（类似Kmeans），旨在最小化节点与最近的聚类中心的距离，即增加簇的内聚度，训练更适合聚类的表示向量。

此外论文中还引入了平滑正则化项（未在上述目标函数公式中给出），该项形式如下：

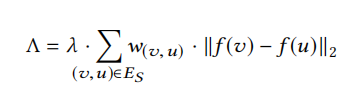
上述函数中用到的符号解释如下：

E_{S}-the\ edges\ within\ the\ windows

w(v,u)-the\ regularization\ weight\ of\ each\ pair\ (v,u)

\lambda-the\ regularization\ coefficient

窗口内存在边的节点对的正则化权重w(v,u)可由如下计算（采用网络中的相似度计算方式确定，如Jaccard系数，即两个节点共同邻居的比例越大，两个节点越相似）：

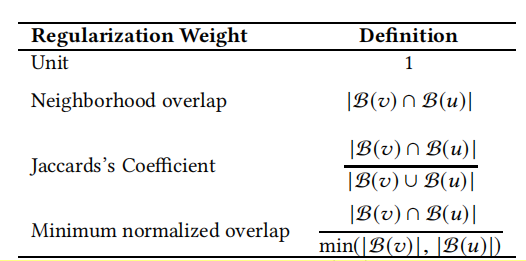
引入该平滑正则化项的目的是使得具有高度重叠邻域的节点对有着更加相似的向量表示。 （该平滑正则化项也可以用于DeepWalk、Node2Vec等目标函数的设计）

因此最终Smooth GEMSEC算法的总的目标函数=共现概率目标+聚类目标+平滑正则化项。

---

(4) 参考文献

Rozemberczki B, Davies R, Sarkar R, et al. Gemsec: Graph embedding with self clustering[C]//Proceedings of the 2019 IEEE/ACM international conference on advances in social networks analysis and mining. 2019: 65-72.

---