clion2020最新安装破解版教程 内含激活码、破解补丁、无限重置时间插件

clion是一款开发C、C++等相关程序的利器，到目前为止已经更新到2020.3版本啦！还没有升级的小伙伴们赶紧升级啦，本文教大家如何安装clion2020.3版本并且破解，此方法亲测100%可以永久激活clion2020.3(其实低版本也可以，包括：2020.2/2020.1/2019等)，教程支持Windows MacOs Linux操作系统！

不用再尝试别人的文章，现在网上大多数文章都是通过破解补丁 + 激活码的方式来进行破解，可以破解到2089年，这种方法看起来是到2089年，但是实际上并不是，Jetbrains官方会不定时封锁激活码，导致通常不过一个月又得更换安装参数，搞得很心烦，不能把时间专注于开发。

本文提供一种全新的方法：即通过重置时间的插件来对clion进行无限时间重置，这样每次启动软件都会有30天的试用期，对用户来说完全是自动的，不用再去操心激活码、安装参数无效的问题，试用也是跟正式是一样的功能，不会有使用上的限制，大家放心！所以仅看本文一篇即可！

免责声明：本教程及相关附件仅限于学术交流，不能用于商业以及违法用途，请于下载后24小时内删除！如产生法律纠纷，一切与本人无关，呼吁各位小伙伴支持下正版软件。本文如有侵权，请联系小编删除之。

插件支持所有操作系统，下面以windows操作系统为例进行演示操作，mac linux操作系统操作类似！

下载安装clion2020.3

1. 先下载安装包，根据自己的系统进行选择下载，官网软件下载地址：【点击跳转】

2. 运行安装包，设置好安装路径，点击 next

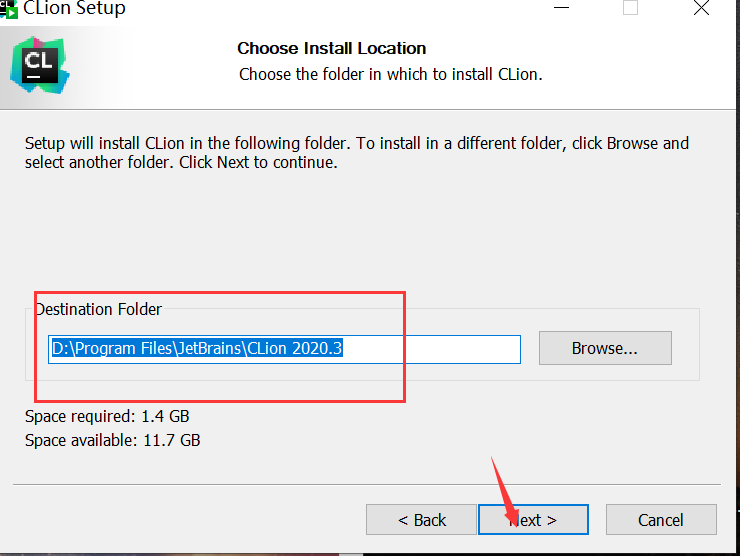
3. 之后的设置可以根据自己的需求进行勾选，一直点击下一步，最后完成安装！

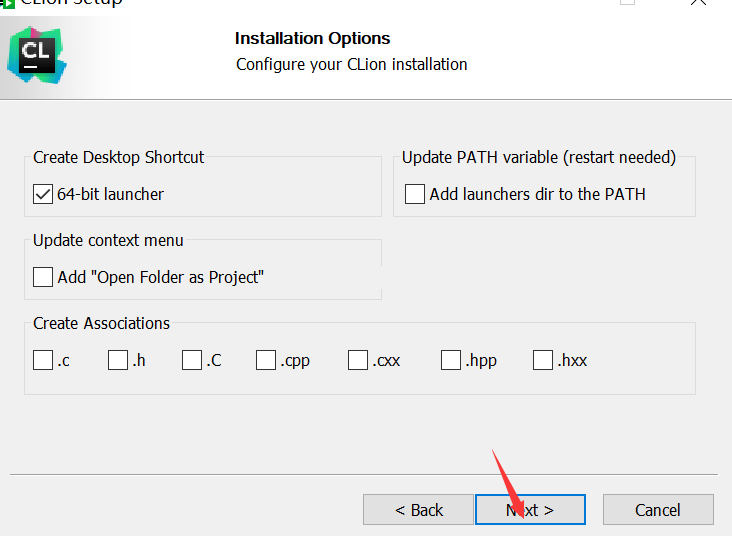
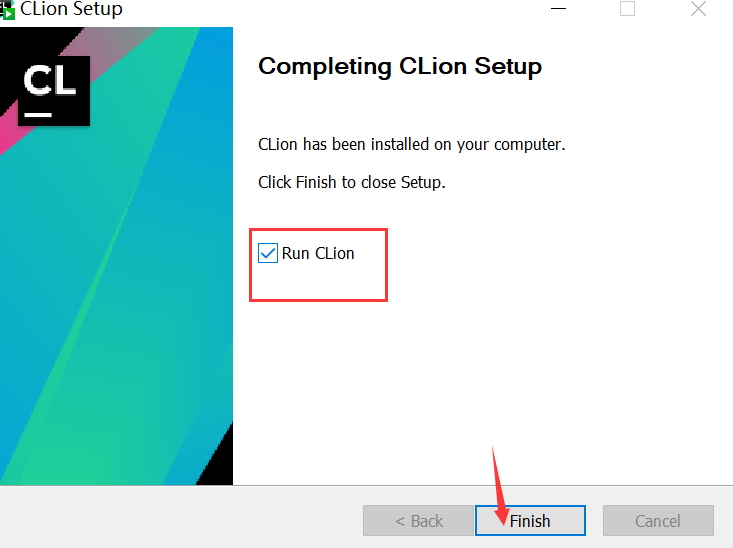
软件安装好后进行破解教程：

1. 下载clion2020无限重置时间插件：【点击下载】(提取码：6666)

2. 打开clion软件，新建一个工程或者打开一个工程进入主页面（如果没法打开先选择试用），从下载的插件包中找到 ide-plugin-2.1.6.zip，用鼠标左键直接拖拽到软件中！

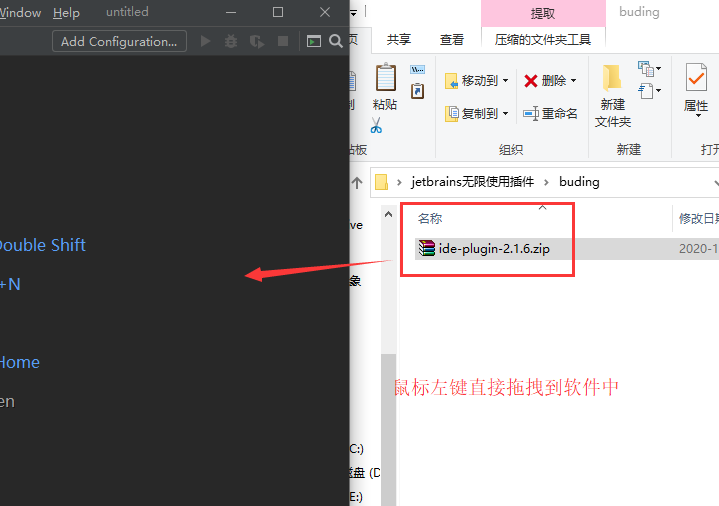
3. 等几秒钟插件就会安装好了，安装好右下角会出现提示并且点击Help会发现多了一个Eval Reset,点击它

4. 在以下对话框中勾选 Auto reset before per restart，点击Reset

5. 点击yes，进行clion软件重启

6. 如出现下框点击Exit退出，至此已经完成破解

7. 重启clion后我们在点击Help-->Eval Reset查看我们的信息，发现上一次重置时间与下一次过期时间都有了变化，一直都是试用30天，到此clion破解激活成功，点击右上角减号即可关闭，正常使用，以后都无需操作，永久破解使用，非常稳定！

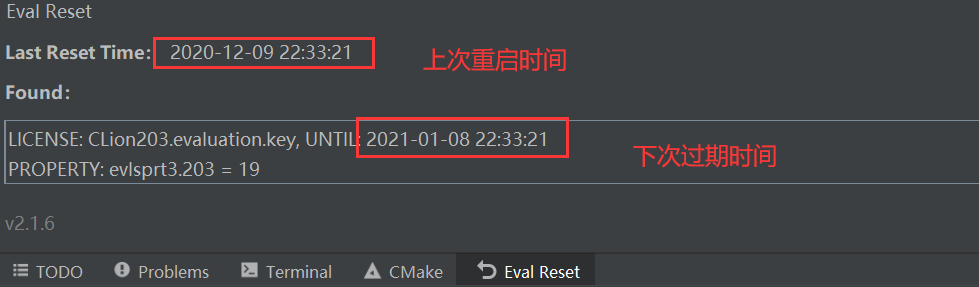
8. 关于插件的更新：

clion会自行检查自身和所有的安装插件并且提示，用户看到提示可以自行选择更新！

或者手动点击Help-->Check for Updates...进行检查，如看到有日志更新即可选择更新，插件更新可能需要重启ide！

小结：小编亲测可以完美激活clion2020，教程简单易用，请各位小伙伴认真执行每一个步骤，最后祝大家成功破解clion软件，^_^