作图直观理解Parzen窗估计（附Python代码）

1.简介

Parzen窗估计属于非参数估计。所谓非参数估计是指，已知样本所属的类别，但未知总体概率密度函数的形式，要求我们直接推断概率密度函数本身。

对于不了解的可以看一下https://zhuanlan.zhihu.com/p/88562356

下面仅对《模式分类》（第二版）的内容进行简单探讨和代码实现

2.窗函数

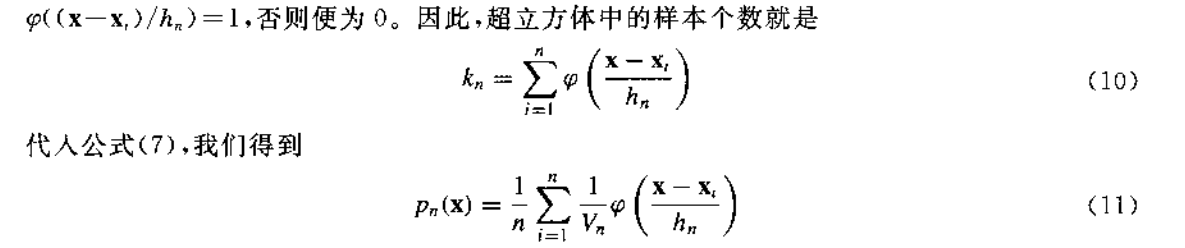
我们不去过多探讨什么是窗函数，只需简单理解这种估计的思想即可。

假设一种情况，你正在屋里看模式分类，结果天降正义掉下来一盆乒乓球，掉的哪里都是，你觉得这是天意，如果很多乒乓球都掉在了一个位置，那么那个位置下一次必掉屠龙宝刀，你想通过估计屋子里乒乓球密度，找出这个位置，那么如何估计呢？

假设你的屋里正好铺了地砖，每块地砖的大小都相同。你此时灵机一动，我只需要统计每块地砖上的乒乓球个数，有最多乒乓球的地砖就是屠龙宝刀的位置。

这似乎听起来很简单，的确，就是这么简单。我们回头看一下公式（9），其中\(
\varphi \left( \mathbf{u} \right)\)其实就是判断某个乒乓球是否在某个地砖上的一个函数，这里的\(\mathbf{u}\)是 乒乓球相对地砖中心的位置。

这里\(\mathbf{u}\)是\(\mathbf{x}-\mathbf{x}_{\mathbf{i}}\)，\(\mathbf{x_i}\)是地砖中心的位置，而\(\mathbf{x}\)是乒乓球的位置。

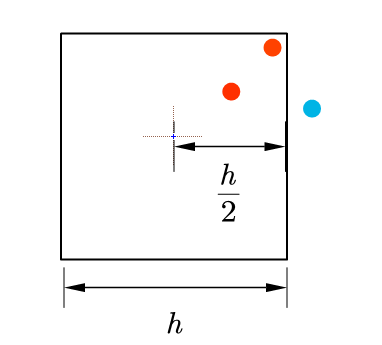
那么公式（9）就显而易见了，如上图所示，你屋子里一块地砖的边长为\({h}\)，红色乒乓球在地砖内，蓝色乒乓球没有在地砖内，判断的条件显然就是向量\(\mathbf{x}-\mathbf{x}_{\mathbf{i}}\)的每个元素是否小于\(\frac{1}{2}h\)，我们可以直接对\(\mathbf{x}-\mathbf{x}_{\mathbf{i}}\)乘以\(\frac{1}{h}\)，这样我们的窗函数就可以写成公式（9）的样子，只需要看参数\(\mathbf{u}=\frac{\mathbf{x}-\mathbf{x}_{\mathbf{i}}}{h}\)的每个元素是否小于\(\frac{1}{2}\)即可。

然后呢？ 到这里工作差不多就结束了，我们看哪块地砖上乒乓球最多就行。

对于某块中心在\(\mathbf{x_i}\)的地砖，地砖上的乒乓球个数\(k\)就是公式（10）

有了每块地砖上的乒乓球个数，概率密度的估计就很简单了。

\[p\left( \mathbf{x} \right) =\frac{k}{nV}\quad V=h^d
\]

一共\(n\)个球，有\(k\)个球落在某个地砖上，地砖的面积为\(V=h^2\)（别忘了地砖是二维空间），那\(p(\mathbf{x})\)就出来了。

到这里，公式（11）也不需要我说什么了吧

• 这里所写的窗函数表示超立方体，而不是超球体，判断条件也不是点到中心的距离小于2/h，而是点坐标的每个元素都小于2/h。

3.大地砖和小地砖

假设400个乒乓球在你房间的大致分为两堆，它们的分布可近似为

\[\left( x_1\sim N\left(-3,4 \right) ,y_1\sim N\left(4,36 \right) \right)
\\
\left( x_2\sim N\left( 5, 4 \right),y_2\sim N\left(-4,25 \right) \right)
\\
\]

乒乓球位置如下图所示

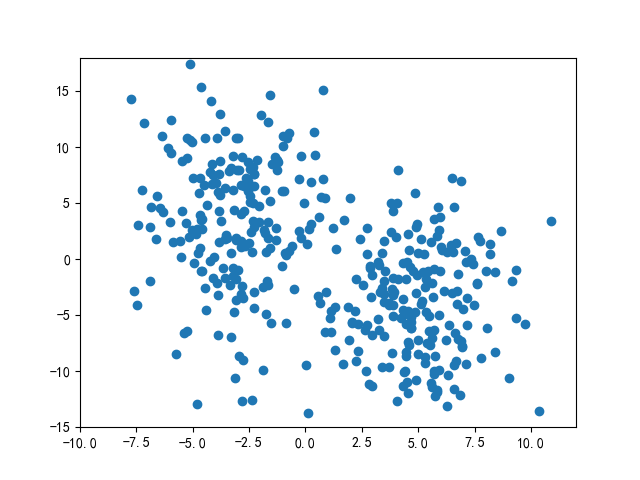
你为了更好的估计乒乓球的密度，用魔法不断更改着地砖的大小，如下图所示，地砖的边长分别为8、5、2，黄点为坐标为(1,4)的地砖所包含的乒乓球，红点为地砖中心。我们可以看到随着\(h\)的不断变化，每个地砖所包含的乒乓球数量是不同的。

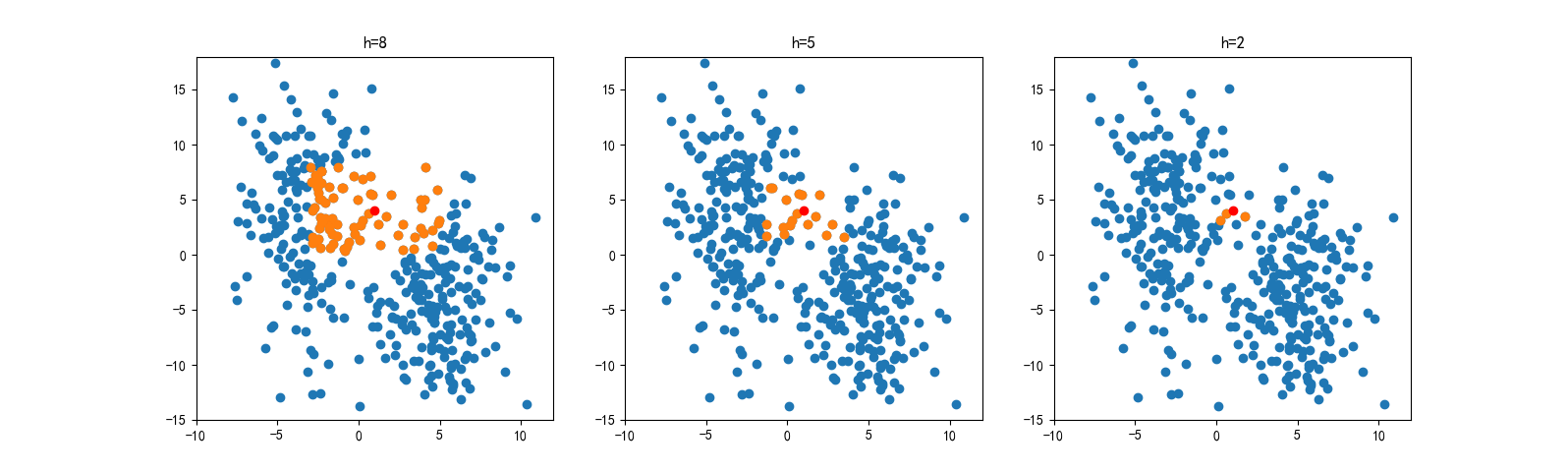
下面我们可以看到三种不同大小的地砖估计出来的概率密度，如下图所示：

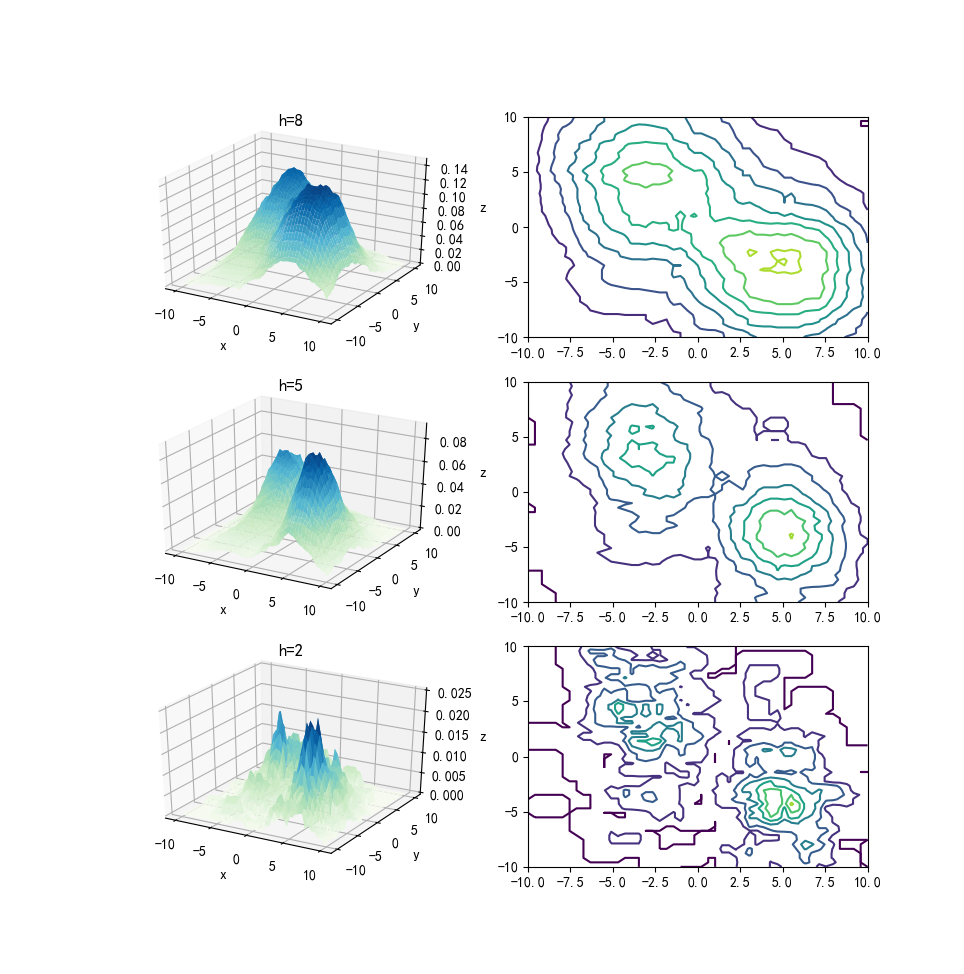
所以说。。咳咳，这里直接放原话。

4.一盆球和无限球

假设我们不再是400个球，我们有。。400000个球，怎么样，真·天降正义，首先乒乓球的分布是这样的：

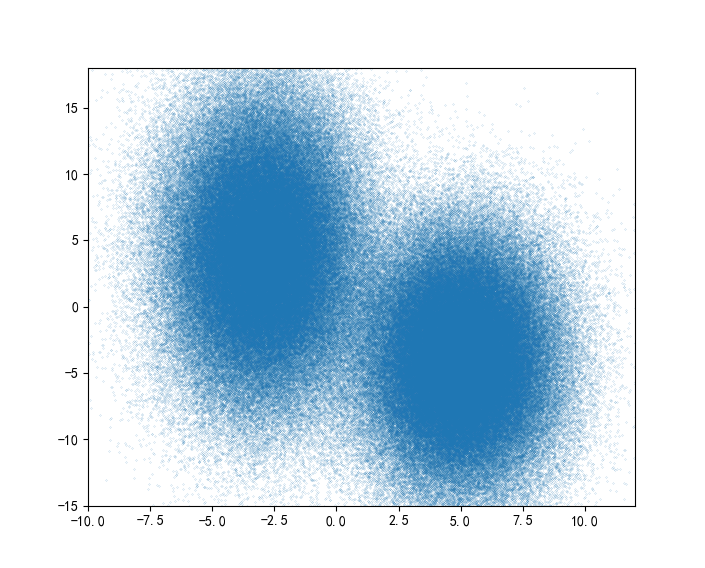
我们再次用边长为8、5、2的地砖对乒乓球进行概率密度估计，如下图所示

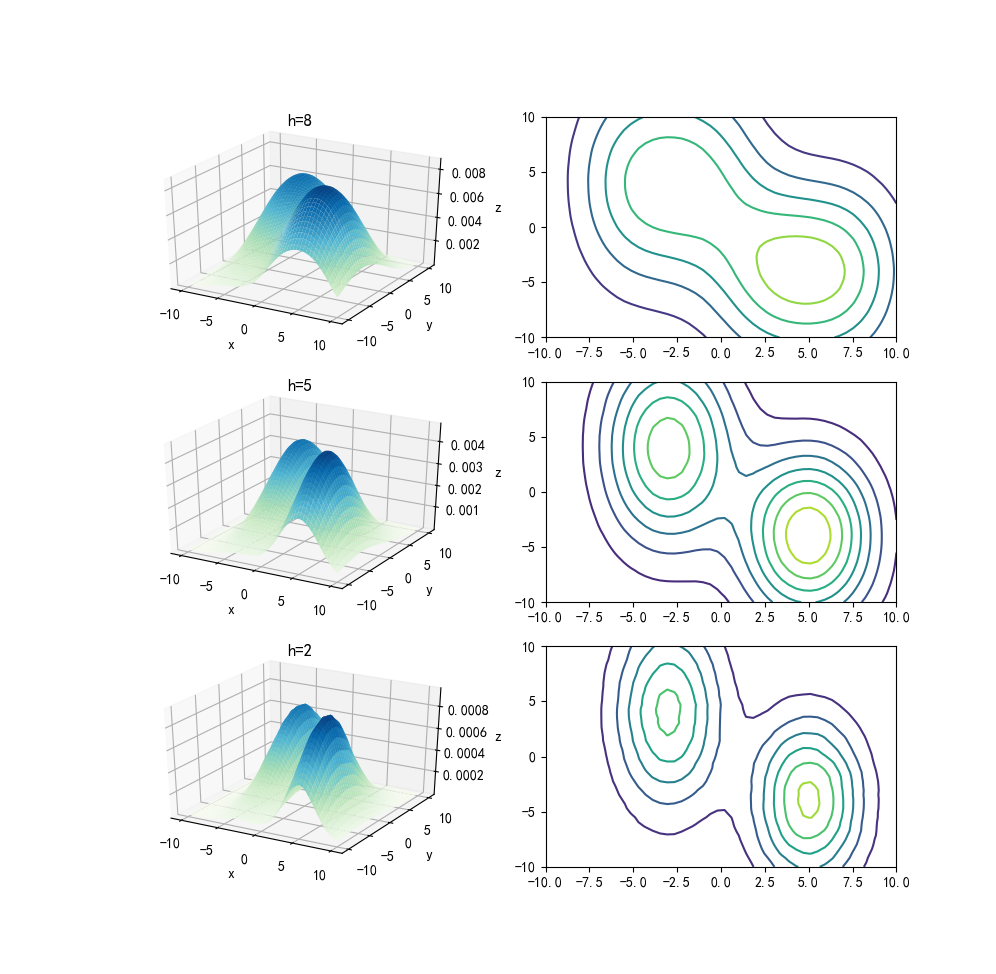
说白了其实都差不多，显而易见的事情，这里再放出一个原话

当n趋近于无穷大时，\(p_n(x)\)将收敛于光滑的\(p(x)\)曲线

代码附录

jupyter格式

环境：python 3.7

#%%
# 生成数据
import matplotlib.pyplot as plt
%matplotlib auto

import numpy as np
n = 200000
datax = np.hstack([np.random.randn(n)*2-3,
                   np.random.randn(n)*2+5])
datay = np.hstack([np.random.randn(n)* 6+4,
               np.random.randn
               (n)*5-4])
xi = np.array([1,4])
xv,yv = datax,datay
pos = np.vstack([datax,datay])

#%%
# 散点图
plt.figure(1)
plot_pos = 131
for h in [8,5,2]:
    plt.subplot(plot_pos)
    plot_pos += 1
    Vn = h ** 2
    u = (pos - xi.reshape(-1,1))/h # u = (x - xi)/h
    ix,iy = pos[:,(abs(u)<=0.5).all(axis=0)]
    plt.xlim([-10,12])
    plt.ylim([-15,18])
    plt.title("h="+str(h))
    plt.scatter(xv,yv,s=0.01)
    plt.scatter(ix,iy)
    plt.scatter(xi[0],xi[1],c='r')
plt.show()

#%%
# 三维概率密度图 和 等高线图
def px(x):
    u = (pos - x.reshape(-1,1))/ h # u = (x - xi)/h
    ix,iy = pos[:,(abs(u)<=0.5).all(axis=0)]
    k = len(ix)
    return k / (Vn * n)

w = 50
gx = gy = np.linspace(-10,10,w)
gxv,gyv = np.meshgrid(gx,gy)

fgxv = gxv.ravel()
fgyv = gyv.ravel()

plt.figure(3)
plot_pos = 321
for i in [8,5,2]:
    h = i
    fpx = np.array([px(x) for x in np.vstack([fgxv,fgyv]).T])
    fpx = fpx.reshape(w,w)
    ax = plt.subplot(plot_pos,projection='3d')
    plot_pos += 1
    ax.plot_surface(gxv,gyv,fpx,cmap='GnBu')
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    ax.set_title('h='+str(h))
    ax = plt.subplot(plot_pos)
    plot_pos += 1
    ax.contour(gxv,gyv,fpx)
plt.show()