Java 树结构的基础部分(一)
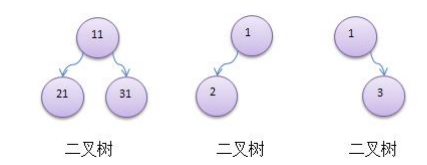
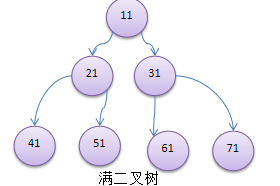
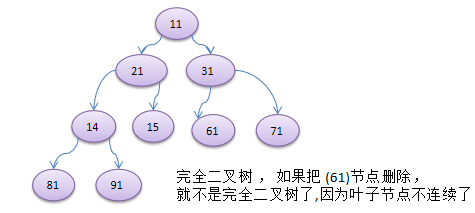

代码实现
在最后面
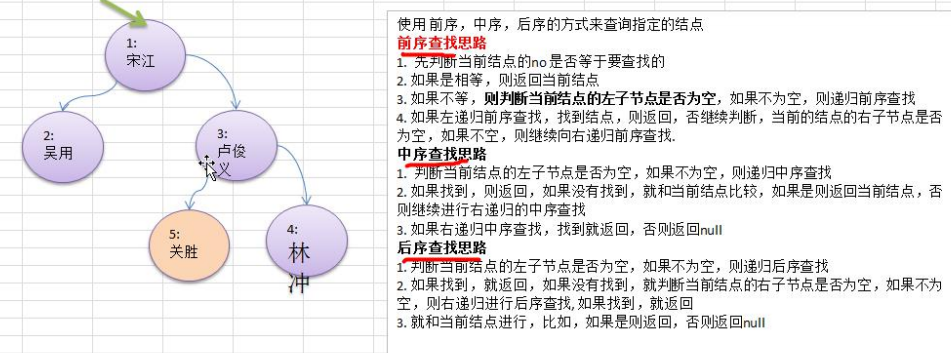

package com.lin.tree_0308;
public class BinaryTreeDemo {
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
HeroNode heroNode1 = new HeroNode(1, "伍六七");
HeroNode heroNode2 = new HeroNode(2, "梅花十一");
HeroNode heroNode3 = new HeroNode(3, "梅花十三");
HeroNode heroNode4 = new HeroNode(4, "江主任");
HeroNode heroNode5 = new HeroNode(5, "希义");
heroNode1.setLeft(heroNode2);
heroNode1.setRight(heroNode3);
heroNode3.setRight(heroNode4);
heroNode3.setLeft(heroNode5);
binaryTree.setRoot(heroNode1);
// System.out.println("前序遍历:");
// binaryTree.preOrder();
// System.out.println("中序遍历:");
// binaryTree.infixOrder();
//
// System.out.println("后序遍历");
// binaryTree.postOrder();
// System.out.println("前序查找:");
// HeroNode preOrderSearch = binaryTree.preOrderSearch(5);
// if(preOrderSearch != null) {
// System.out.println(preOrderSearch);
// } else {
// System.out.println("没有找到");
// }
// System.out.println("中序查找:");
// HeroNode infixOrderSearch = binaryTree.infixOrderSearch(5);
// if(infixOrderSearch != null) {
// System.out.println(infixOrderSearch);
// } else {
// System.out.println("没有找到");
// }
//
// System.out.println("后序查找:");
// HeroNode postOrderSearch = binaryTree.postOrderSearch(5);
// if(postOrderSearch != null) {
// System.out.println(postOrderSearch);
// } else {
// System.out.println("没有找到");
// }
System.out.println("删除前");
binaryTree.preOrder();
binaryTree.delNode(2);
System.out.println("删除后");
binaryTree.preOrder();
}
}
class BinaryTree{
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
// 删除节点
public void delNode(int no) {
if (root != null) {
// 如果只有一个root
if (root.getNo() == no) {
root = null;
} else {
root.delNode(no);
}
} else {
System.out.println("空树!");
}
}
// 前序遍历
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空!");
}
}
// 中序遍历
public void infixOrder() {
if(this.root != null) {
this.root.infixOrder();
} else {
System.out.println("二叉树为空!");
}
}
// 后序遍历
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
} else {
System.out.println("二叉树为空!");
}
}
// 前序查找
public HeroNode preOrderSearch(int no) {
if(root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
// 中序查找
public HeroNode infixOrderSearch(int no) {
if (root != null) {
return root.infixOrderSearch(no);
} else {
return null;
}
}
// 后序查找
public HeroNode postOrderSearch(int no) {
if (root != null) {
return root.postOrderSearch(no);
} else {
return null;
}
}
}
class HeroNode{
private String name;
private int no;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [name=" + name + ", no=" + no + "]";
}
// 前序遍历
public void preOrder() {
System.out.println(this); // 输出父节点
if(this.left != null) {
this.left.preOrder();
}
if(this.right != null) {
this.right.preOrder();
}
}
// 中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this); // 输出父节点
if (this.right != null) {
this.right.infixOrder();
}
}
// 前序遍历
public void postOrder() {
if (this.left != null) {
this.left.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this); // 输出父节点
}
// 前序查找
public HeroNode preOrderSearch(int no) {
System.out.println("1");
// 比较当前节点是不是
if(this.no == no) {
return this;
}
// 1 判断当前节点的左节点是否为空,如果不为空,则递归前序查找
// 2 如果左递归前序查找,找到节点,则返回
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode != null) {// 说明左子树找到了
return resNode;
}
// 1 左递归如果没有找到,则继续判断
// 2 当前节点的右节点是否为空,如果不为空,则继续向右递归前序查找
if(this.right != null) {
resNode = this.right.preOrderSearch(no);
}
// 这时候不管有没有找到都要返回resNode
return resNode;
}
// 中序查找
public HeroNode infixOrderSearch(int no) {
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("1");
if(this.no == no) {
return this;
}
if(this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
// 后序查找
public HeroNode postOrderSearch(int no) {
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
if(this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("1");
if(this.no == no) {
return this;
}
// 如果都没有找到
return resNode;
}
/**
*
* @Description:1 因为我们的二叉树是单向,所以我们是判断当前节点的子节点是否需要删除节点,而不是直接去判断当前节点是否需要删除节点。<br>
* 2 如果当前节点的左子节点不为空,并且左子节点就是要删除节点,就将this.left = null;并且就返回(结束递归删除) <br>
* 3 如果当前节点的右子节点不为空,并且右子节点就是要删除节点,就将this.right = null;并且就返回(结束递归删除) <br>
* 4 如果第2和第3都没有删除节点,那么我们就需要向左子树进行递归删除<br>
* 5 如果第4补也没有删除节点,则向右子树进行递归删除<br>
* @author LinZM
* @date 2021-3-8 15:17:32
* @version V1.8
*/
public void delNode(int no) {
if(this.left != null && this.left.no == no) {
this.left = null;
return;
}
if(this.right != null && this.right.no == no) {
this.right = null;
return;
}
if(this.left != null) {
this.left.delNode(no);
}
if(this.right != null) {
this.right.delNode(no);
}
}
}
仅供参考,有错误还请指出!
有什么想法,评论区留言,互相指教指教。
觉得不错的可以点一下右边的推荐哟
Java 树结构的基础部分(一)的更多相关文章
- Java 树结构的基础部分(二)
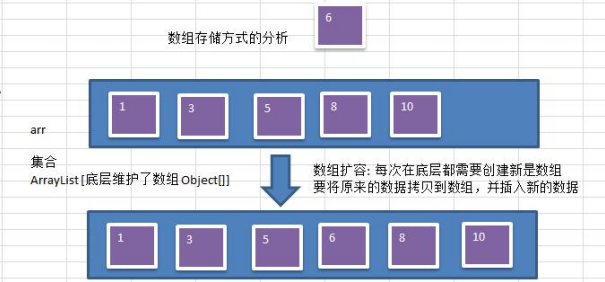
1 顺序存储二叉树 1.1 顺序存储二叉树的概念 基本说明 从数据存储来看,数组存储方式和树的存储方式可以相互转换,即数组可以转换成树,树也可以转换成数组, 看下面的示意图. 要求: 1) 右 ...
- 如何夯实(Java)编程基础,并深入学习和提高
如何夯实(Java)编程基础,并深入学习和提高? 240赞同反对,不会显示你的姓名 匿名用户 240 人赞同 多学习...网上自学的学习网站很多,见以下榜单~一.汇总榜单: 公开课_学习网站导航 收录 ...
- Java开发的基础条件:
------------Java开发的基础条件:Java相关的基础+对编程的自己的理解+调试代码+自己的坚持 一定要谦逊,不人云亦云,不去妄言某一门语言或技术好或坏!不是哪门技术有问题,而是(不会用才 ...
- Java多线程系列--“基础篇”11之 生产消费者问题
概要 本章,会对“生产/消费者问题”进行讨论.涉及到的内容包括:1. 生产/消费者模型2. 生产/消费者实现 转载请注明出处:http://www.cnblogs.com/skywang12345/p ...
- Java多线程系列--“基础篇”04之 synchronized关键字
概要 本章,会对synchronized关键字进行介绍.涉及到的内容包括:1. synchronized原理2. synchronized基本规则3. synchronized方法 和 synchro ...
- Java多线程系列--“基础篇”02之 常用的实现多线程的两种方式
概要 本章,我们学习“常用的实现多线程的2种方式”:Thread 和 Runnable.之所以说是常用的,是因为通过还可以通过java.util.concurrent包中的线程池来实现多线程.关于线程 ...
- Java多线程系列--“基础篇”03之 Thread中start()和run()的区别
概要 Thread类包含start()和run()方法,它们的区别是什么?本章将对此作出解答.本章内容包括:start() 和 run()的区别说明start() 和 run()的区别示例start( ...
- Java多线程系列--“基础篇”05之 线程等待与唤醒
概要 本章,会对线程等待/唤醒方法进行介绍.涉及到的内容包括:1. wait(), notify(), notifyAll()等方法介绍2. wait()和notify()3. wait(long t ...
- Java多线程系列--“基础篇”06之 线程让步
概要 本章,会对Thread中的线程让步方法yield()进行介绍.涉及到的内容包括:1. yield()介绍2. yield()示例3. yield() 与 wait()的比较 转载请注明出处:ht ...
随机推荐
- Linux-字符处理命令
目录 1.sort(排序) 2.uniq(不相邻的两行重复不会去除) 3.cut(取列,截取字段) 4.wc(统计行.单词.字符数) 1.sort(排序) 选项: -t # 指定分隔符 -k # 指定 ...
- 2019牛客多校第二场F Partition problem(暴搜)题解
题意:把2n个人分成相同两组,分完之后的价值是val(i, j),其中i属于组1, j属于组2,已知val表,n <= 14 思路:直接dfs暴力分组,新加的价值为当前新加的人与不同组所有人的价 ...
- Linux内核实现透视---软中断&Tasklet
软中断 首先明确一个概念软中断(不是软件中断int n).总来来说软中断就是内核在启动时为每一个内核创建了一个特殊的进程,这个进程会不停的poll检查是否有软中断需要执行,如果需要执行则调用注册的接口 ...
- Oh My Zsh All In One
Oh My Zsh All In One https://ohmyz.sh/ install # CURL $ sh -c "$(curl -fsSL https://raw.github. ...
- element-ui & babel-plugin-component config bug
element-ui & babel-plugin-component config bug vue-cli bad babel.config.js module.exports = { pr ...
- Python Quiz & Python Exercise
Python Quiz & Python Exercise https://www.w3schools.com/quiztest/quiztest.asp?qtest=PYTHON https ...
- record terminal sessions
record terminal sessions asciinema https://asciinema.org/ # install $ brew install asciinema # Start ...
- svg opacity & fill-opacity & stroke-opacity
svg opacity & fill-opacity & stroke-opacity opacity = ill-opacity + stroke-opacity https://s ...
- 观点纠正,yarn和npm对比,今天yarn仍然比npm快吗
yarn和npm的区别和对比,网上很多了,不多说了. 只纠正一个观点:yarn仍然比npm快吗?不. 2016年,yarn刚刚发布,速度确实比npm快,于是网络上出现了好多推荐yarn的文章. 于是很 ...
- 前端监控SDK开发分享
目录 前言 收集哪些数据 性能 错误 辅助信息 小结 客户端SDK(探针)相关原理和API Web 微信小程序 编写测试用例 单元测试 流程测试 提供Web环境的方式 Mock Web API的方式 ...
