概率派VS贝叶斯派

机器学习中的MLE和MAP两大学派的争论：

频率学派 - Frequentist - Maximum Likelihood Estimation (MLE，最大似然估计)：

频率学派认为世界是确定的，有一个本体，这个本体的真值是不变的，我们的目标就是要找到这个真值或真值所在的范围。

贝叶斯学派 - Bayesian - Maximum A Posteriori (MAP，最大后验估计)_：

贝叶斯学派认为世界是不确定的，人们对世界先有一个预判，而后通过观测数据对这个预判做调整，我们的目标是要找到最优的描述这个世界的概率分布。

在对事物建模时，用θ表示模型的参数，请注意，解决问题的本质就是求θ。那么：

---

频率学派：存在唯一真值θ。当数据量趋于无穷时，这种方法能给出精准的估计；然而缺乏数据时则可能产生严重的偏差。

---

贝叶斯学派： θ是一个随机变量，符合一定的概率分布。在贝叶斯学派里有两大输入和一大输出，输入是先验 (prior)和似然 (likelihood)，输出是后验 (posterior)。

先验，即P(θ)，指的是在没有观测到任何数据时对θ的预先判断，似然，即P(X|θ)，是假设θ已知后我们观察到的数据应该是什么样子的；后验，即P(θ|X)，是最终的参数分布。

                                                               

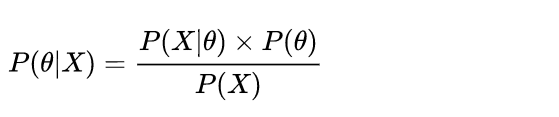
                                      随着数据量的增加，参数分布会越来越向数据靠拢，先验的影响力会越来越小