高阶Laplace曲面形变算法（Polyharmonic Deformation）

　　数学上曲面的连续光滑形变可以通过最小化能量函数来建模得到，其中能量函数用来调节曲面的拉伸或弯曲程度，那么能量函数最小化同时满足所有边界条件的最优解就是待求曲面。

　　能量函数通常是二次函数形式：

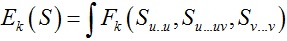
其中S_*代表关于曲面参数u和v的k阶偏导。

　　对于上述优化问题的求解方法，通常利用变分法得到对应的Euler-Lagrange方程，然后求解该方程得到最优解。对于二次能量函数形式，其对应的Euler-Lagrange方程为如下多阶调和方程：

　　例如对于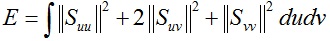，那么对应的Euler-Lagrange方程就是2阶Laplace方程Δ²x = 0。上式中Δ代表Laplace算子，边界区域δΩ的限制条件b_j保证了系统存在非平凡解。

　　对于k = 1，上述方程描述的是满足曲面面积最小的表面；对于k = 2，方程描述的是满足曲面弯曲最小的表面，对于k = 3，方程描述的是满足曲面曲率变化最小的表面。

　　方程的边界条件可以选择Dirichlet边界条件（第一类边界条件），即指定曲面边界点的位置，或者Neumann 边界条件（第二类边界条件），即指定曲面边界点的法向方向。

　　如果曲面用三角网格形式表示，那么我们在方程中需要使用离散Laplace算子，这是一个线性算子，具体形式在“网格形变算法”中有所解释，其表达式如下：

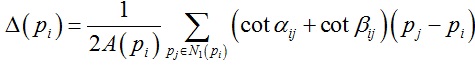
其中α_ij和β_ij为边e_ij对应的2个对角，N₁(p_i)表示顶点p_i的1环邻域点，A(p_i)表示顶点p_i的Voronoi面积。

function L = Laplace_Matrix(V, F)
    nV = size(V,);
    L = sparse(nV,nV);
    for i = :
       i1 = mod(i-,)+;
       i2 = mod(i  ,)+;
       i3 = mod(i+,)+;
       Vec1 = V(F(:,i2),:) - V(F(:,i1),:);
       Vec2 = V(F(:,i3),:) - V(F(:,i1),:);

       cotangle = 0.5 .* dot(Vec1, Vec2, ) ./ norm(cross(Vec1, Vec2, ));

       L = L + sparse(F(:,i2), F(:,i3), cotangle, nV, nV);
    end
    L = L + L';
    L = -spdiags(full( sum(L,) ), , nV, nV) + L;
end

　　利用离散线性Laplace算子，方程可以变化为稀疏线性方程组：

其中p = (p₁, … , p_p)是计算域内的待求点，对应下图中黄色点集；h = (h₁, … , h_p)是计算域内的控制点，对应下图中红色和蓝色点集，它们代表了方程中的边界条件。需要注意的是为满足求解得到的曲面C^k连续，方程中需要待求点外k+1环的控制点集作为边界条件。

 

 

 

 

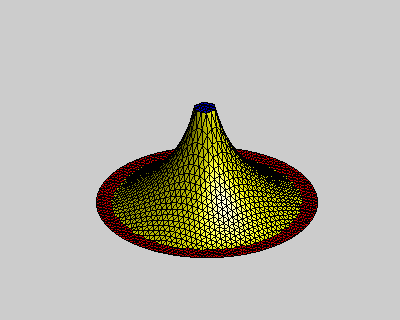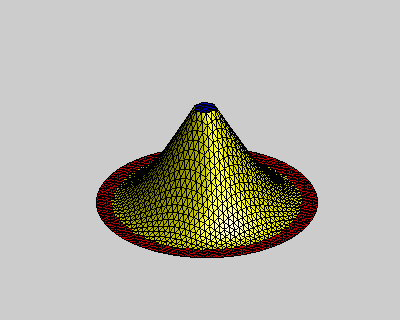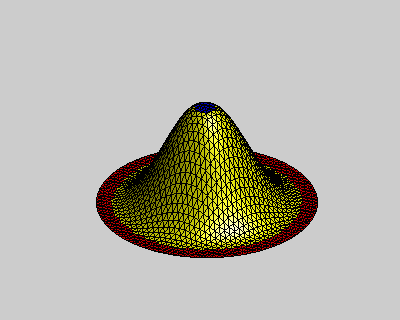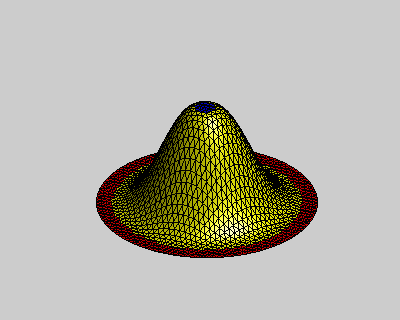
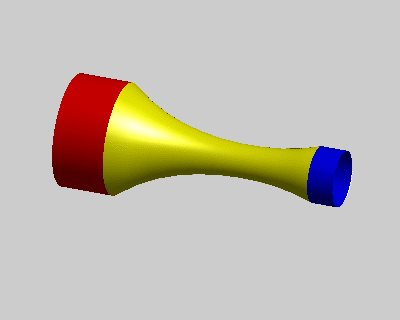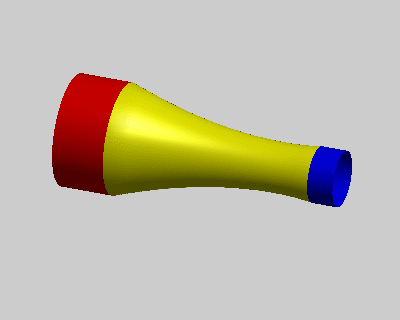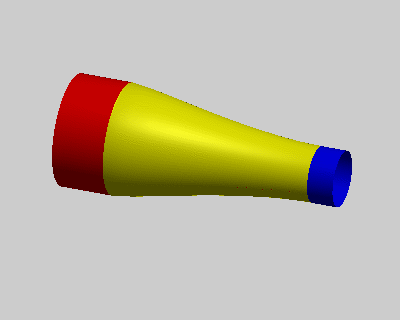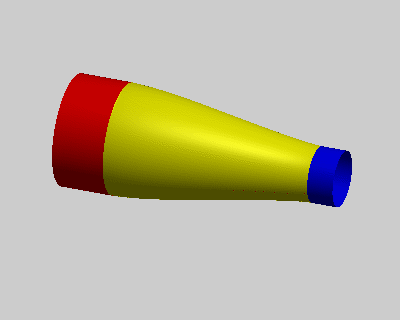
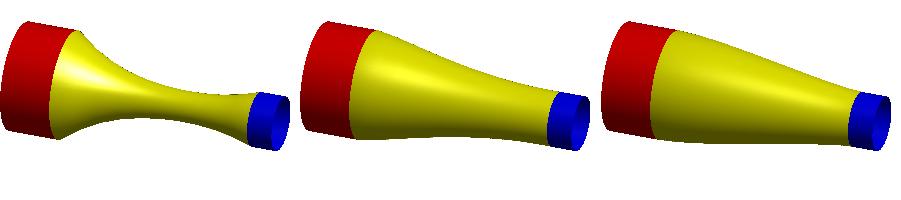
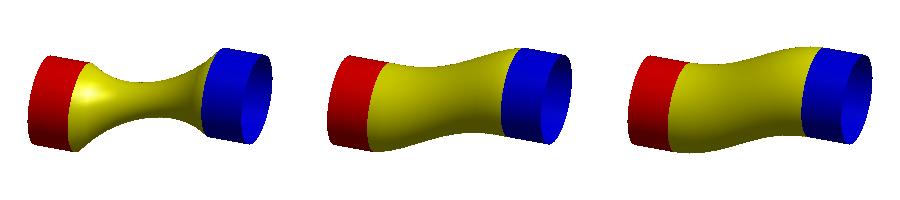
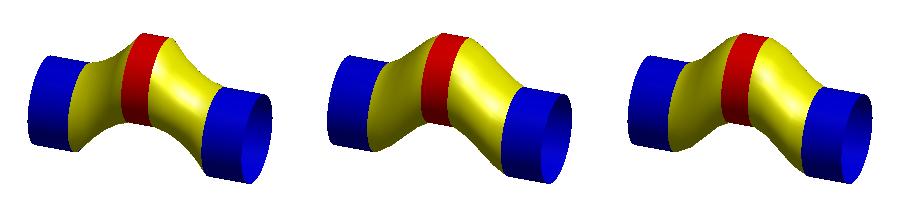
图：k阶能量方程使得曲面边界满足C^k-1连续

左：k = 1，中：k = 2，右：k = 3

本文为原创，转载请注明出处：http://www.cnblogs.com/shushen

参考文献：

[1] Mario Botsch and Leif Kobbelt. 2004. An intuitive framework for real-time freeform modeling. ACM Trans. Graph. 23, 3 (August 2004), 630-634.