BST（二叉搜索树）

BST

基础芝士

给定一棵二叉树，每个节点有权值，定义“BST 性质”为：

对于树中的任意一个节点 \(x\) 都有：

• \(x\) 的权值大于 \(x\) 的左子树中任意节点的权值。
• \(x\) 的权值小于 \(x\) 的右子树中任意节点的权值。

即 \(左子树任意点的权值 < x < 右子树任意点的权值\)。

满足上述性质的二叉树即为“二叉搜索树”(BST)。可以发现，二叉搜索树的中序遍历的点权值单调递增。

一般情况下 BST 中无相同权值，当然有相同权值的也可以处理为无相同权值的。如图：

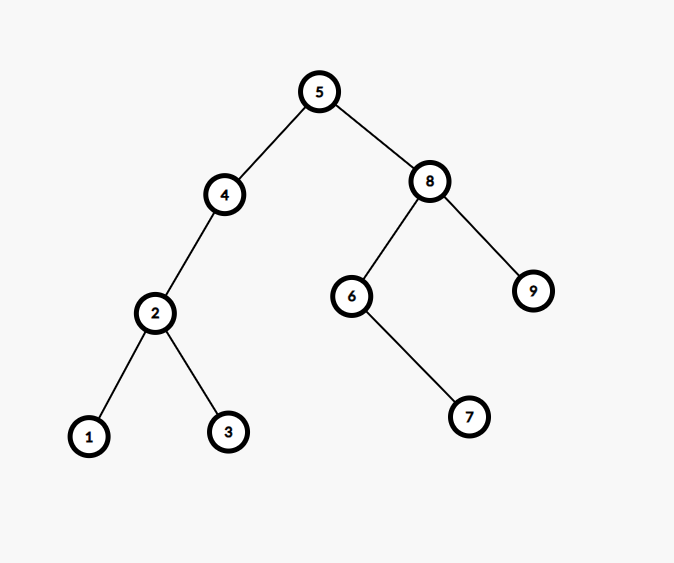
中序遍历结果为 \({1,2,3,4,5,6,7,8,9}\)。

维护操作

建立

为避免越界，一般在 BST 中插入正负无穷。仅由这两个节点构成的 BST 即为空 BST。如图：

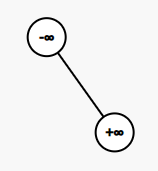
建立的操作即为建立一个空 BST：

const int inf=1<<30;
struct bst
{
    int l,r,v;
}a[N];
int tot,root;

int New(int v)
{
    a[++tot].v=v;
    return tot;
}
void build()
{
    New(-inf),New(inf);
    root=1,a[1].r=2;
}

查找

查找 BST 中是否存在权值为 \(v\) 的节点。从根节点开始，利用“BST 性质”，一层层往下查找。

设当前所在节点为 \(x\)，权值为 \(y\)：

1. \(y=v\)，则已找到。
2. \(y>v\)，若 \(x\) 无左儿子，则说明不存在；若 \(x\) 有左儿子，进入左子树继续查找。
3. \(y<v\)，若 \(x\) 无右儿子，则说明不存在；若 \(x\) 有右儿子，进入右子树继续查找。

用递归实现：

int find(int x,int v)
{
    int y=a[x].v;
    if(y==v) return x;
    if(x==0) return 0; //若x不存在
    return y>v ? find(a[x].l,v) : find(a[x].r,v);
}

用 while 实现：

int find(int v)
{
    int x=root;
    while(x)
    {
        int y=a[x].v;
        if(y==v) break;
        x= y>v ? a[x].l : a[x].r;
    }
    return x;
}

插入

在 BST 中插入一个权值为 \(v\) 的点（假设原来不存在）。

类似于查找操作：

设当前所在节点为 \(x\)，权值为 \(y\)：

1. \(y>v\)，进入左子树继续查找。
2. \(y<v\)，进入右子树继续查找。
3. 若接下来进入的点为空，则直接建立。
   
   用递归实现：

int insert(int &x,int v)//使用&，更新其父节点的信息
{
    int y=a[x].v;
    if(y==v) return ;
    if(x==0)
    {
        x=New(v);
        return ;
    }
    return y>v ? insert(a[x].l,v) : insert(a[x].r,v);
}

求最大/最小值

求以节点 \(x\) 为根节点的树的最大/最小值。在 BST 中，任一子树都是 BST，而 BST 的最小值一定在最左边的点上，最大值一定在最右边的点上（“BST 性质”）。如图：



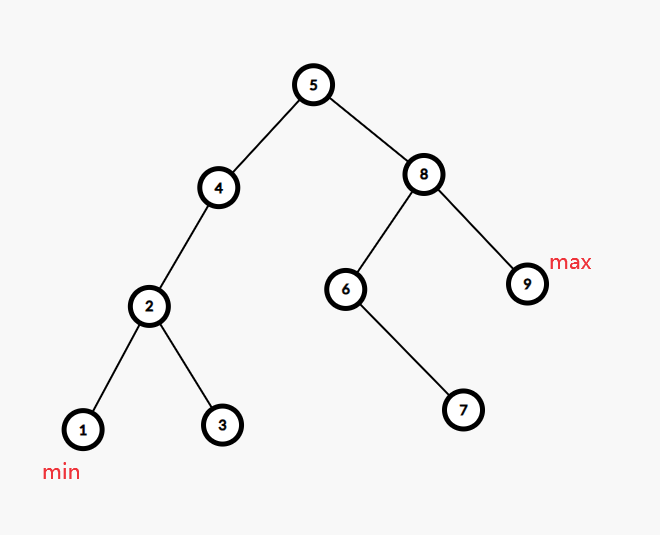
则求最大值就是从 \(x\) 开始一直向左子树走直到没有左子树，求最小值就是从 \(x\) 开始一直向右子树走直到没有右子树，当然要注意避开正负无穷。

int get_min(int x)
{
    while(a[x].l) x=a[x].l;
    return x;
}
int get_max(int x)
{
    while(a[x].r) x=a[x].r;
    return x;
}

求前驱/后继

设节点为 \(x\)，权值为 \(y\)。

• \(x\) 的前驱：指中序遍历 BST 后，位于 \(x\) 前的第一个点，即满足 \(v<y\) 的最大的 \(v\) 所对应的节点。
• \(x\) 的后继：指中序遍历 BST 后，位于 \(x\) 后的第一个点，即满足 \(v>y\) 的最小的 \(v\) 所对应的节点。

因此，求 \(x\) 的前驱即求 \(x\) 左子树中的最大值，求 \(x\) 的后继即求 \(x\) 右子树中的最小值。

int get_pre(int x)
{
    return get_max(a[x].l);
}
int get_ne(int x)
{
    return get_min(a[x].r);
}

若给出的是 \(y\)：

int get_pre(int u,int v)
{
    if(u==0) return -inf;
    if(a[u].v>=v) return get_pre(a[u].l,v);//先找到左子树
    return max(a[u].v,get_pre(a[u].r,v));//再找到最大值
}
int get_ne(int u,int v)
{
    if(u==0) return inf;
    if(a[u].v<=v) return get_ne(a[u].r,v);//先找到右子树
    return min(a[u].v,get_ne(a[u].l,v));//再找最小值
}

删除

从 BST 中删除权值为 \(v\) 的节点 \(x\)。

思考如何在删除 \(x\) 后能维护 BST。

• 若 \(x\) 的儿子个数小于2，则直接用 \(x\) 的儿子代替 \(x\) 的位置，与 \(x\) 的父节点相连。
• 若 \(x\) 的儿子个数等于2，考虑删除后，应该是 \(x\) 的后继 \(next\) 代替它的位置，也就是要先删除 \(next\)，再用 \(next\) 代替 \(x\)。而且 \(next\) 无左儿子，因为 \(next\) 是 \(x\) 右子树的最小值。所以，用 \(next\) 的右儿子代替 \(next\) 的位置，再用 \(next\) 代替 \(x\) 的位置。

void remove(int v)
{
    int &x=root;//同时修改x父节点的信息
    while(x)
    {
        int y=a[x].v;
        if(y==v) break;
        x= y>v ? a[x].l : a[x].r;
    }
    if(x==0) return;
    if(a[x].l==0) x=a[x].r;
    else if(a[x].r==0) x=a[x].l;
    else
    {
        int next=get_ne(x);
        remove(a[next].v);
        a[next].l=a[x].l,a[next].r=a[x].r;
        x=next;
    }
}

结语

BST 中每一次操作的期望复杂度为 \(O(\log{n})\)，但 BST 容易退化。当 BST 为一条链时，复杂度为 \(O(n)\)。为了解决该问题，出现了各种平衡二叉树，请看：

tips

点权值中需满足“BST性质”的称为“关键码”，平衡二叉树中会区分开。