[C++]二叉链-二叉树存储

二叉链存二叉树

预备知识

• 指针的熟练掌握
  • Bolg
• template模板的知识
  • Bolg
• 二叉树的基本知识

感谢：

代码参考：CSDN博主「云雨澄枫」的原创文章

链接

代码解析

结构体 BiNode

template<class T>
struct BiNode{
	T data;
	BiNode<T> *lchild,*rchild;
};

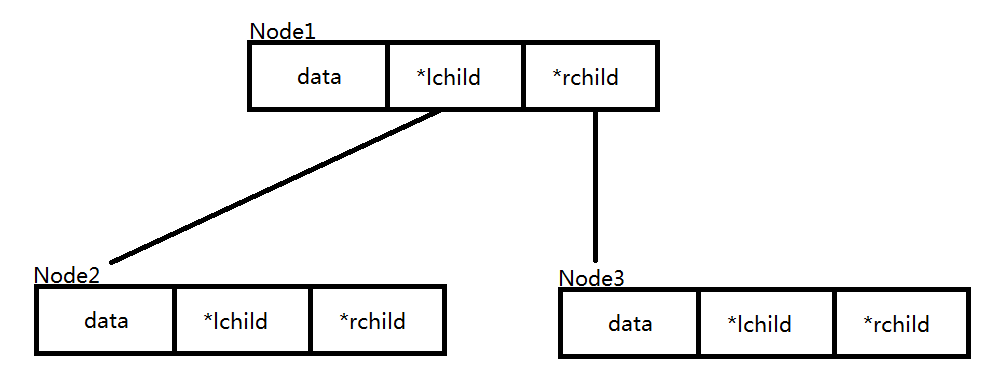
Node 结点

这个结构体就是用来存储二叉链的每一个节点的

• data

表示这个节点所存的值

• *lchild & *rchild

表示指向 左子树 和 右子树 的指针

这样的结构能很好地存下二叉树：

（具体的建树方法会放在后面解释）

类 BiTree

template <class T>
class BiTree{
public:
	//构造 & 折构
	BiTree(){root = Creat(root);}
	~BiTree(){Release(root);}
	//遍历
	void PreOrder(){PreOrder(root);}
	void InOrder(){InOrder(root);}
	void PostOrder(){PostOrder(root);}
	void LeverOrder();
	//树的深度
	int  Depth(){Depth(root);}
	//叶子结点数量
	void CaculateLeafNum(){CaculateLeafNum(root);}
	//交换左右子树
	void swap(){swap(root);}
private:
	BiNode<T> *root;//<-根节点在这里
	BiNode<T> *Creat(BiNode<T> *bt);
	void Release(BiNode<T> *bt);
	void PreOrder(BiNode<T> *bt);
	void InOrder(BiNode<T> *bt);
	void PostOrder(BiNode<T> *bt);
	int  Depth(BiNode<T> *root);
	void CaculateLeafNum(BiNode<T>* root);
	void swap(BiNode<T> *root);
};

这便是树的主体

一个 BiTree 的类就代表一颗二叉树

• public

在这里定义了一些之后会用到的函数以及构造函数和折构函数

这里知道有这些东西即可

• private

这里则有一些 public 会用到的函数

以及这个树的根节点

构造函数 & 折构函数

1. 构造函数

在类中 是这样写的：

BiTree(){root = Creat(root);}

构造这个树是通过 Creat 这个函数来实现的

Creat_Code:

template <class T>
BiNode<T> *BiTree<T>::Creat(BiNode<T> *bt)
{
	T t;
    cin >> t;
    if(t == '#')
		bt = NULL;
    else {
    	bt = new BiNode<T>;
		bt->data = t;
    	bt->lchild = Creat(bt->lchild);
    	bt->rchild = Creat(bt->rchild);
    }
    return bt;
}

在讲构造函数之前

还需要提一嘴其输入方式

这里是采用前序遍历的方式进行输入

同时还需要以 "#" 输入叶子结点的空子结点

例子：

cin：

ABD#G###CE##F##

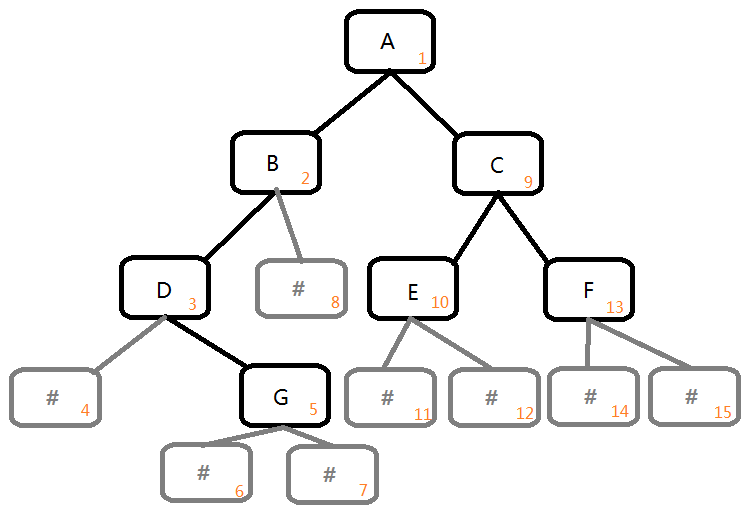
• 图中的序号即代表 cin 中的第几个字符

知道了输入的顺序之后

代码就变得好理解很多了

创建一个结点的时候

首先输入这个结点的值（就是 t）

若其值是 "#" 那就不继续往下面创造新结点了

直接让 bt 为 空指针

并把这个指针返回

若其值不为 "#"

那说明后面可能还有结点需要添加

就继续在左右子结点上调用 Creat函数

bt = new BiNode<T>;

这行代码可能还需要解释一下

new 是用来开辟新的内存空间的关键字

这里相当于开辟了一个新的结点结构体

而 bt 存下了这个结点结构体的指针

1. 折构函数

~BiTree(){Release(root);}

折构函数和构造函数一样是用类名来作为函数名的

不过需要在前面加一个 "~"

这个函数调用了 Release 这个函数

template<class T>
void BiTree<T>::Release(BiNode<T> *bt){
	if(bt != NULL){
		Release(bt->lchild);
		Release(bt->rchild);
		delete bt;
	}
}

delete 用于删除内存的关键词

这个函数因该很好理解

就是从上往下搜

从下往上删

就不过多解释了

遍历函数

这个分两部分将

第一部分 : 前/中/后序遍历

这些代码原理相同 就随便挑一个讲好了

template <class T>
void BiTree<T>::PreOrder(BiNode<T> *bt){
    if (bt == NULL)
		return;
    else {
        cout << bt->data;
        PreOrder(bt->lchild);
        PreOrder(bt->rchild);
	}
}

从 root结点 开始搜索

如果不是空结点 那就直接输出

然后往两边找

决定前中后的只在于

输出与往两侧搜索语句的顺序

第二部分 : 层序遍历

还是用这个图

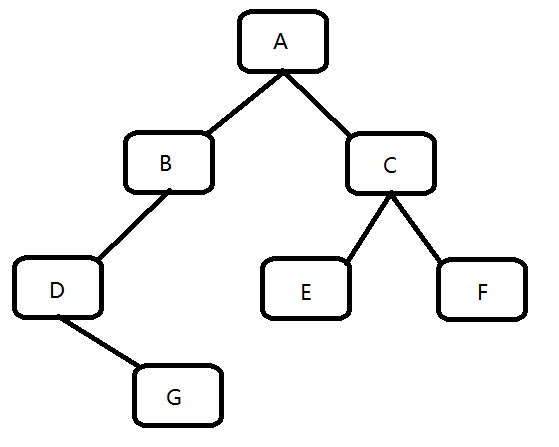
Code:

template<class T>
void BiTree<T>::LeverOrder(){
	int front = -1,rear = -1;
	BiNode<T> *Q[100];

	if(root == NULL) return;
	Q[++rear] = root;
	while(front != rear){
		BiNode<T> *q = Q[++front];
		cout << q->data;
		if(q->lchild != NULL) Q[++rear] = q->lchild;
		if(q->rchild != NULL) Q[++rear] = q->rchild;
	}
}

这里是用一个数组和两个变量来实现了队列的功能

接下来我们来模拟一下

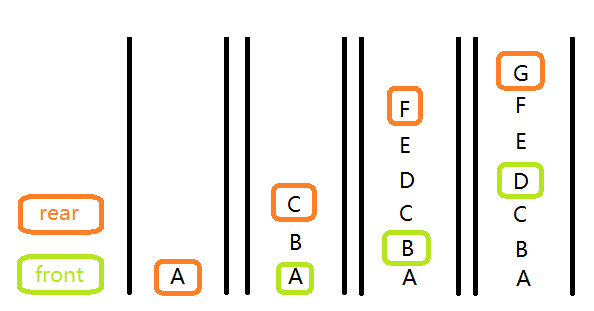
这样就可以实现层序遍历了

求树的深度

Code：

template<class T>
int BiTree<T>::Depth(BiNode<T> *root){
	int hl,hr;
	if(root == NULL)
		return 0;
	else{
		hl = Depth(root->lchild);
		hr = Depth(root->rchild);
		return max(hl,hr) + 1;
	}
}

深度要找的是最深的叶子结点的层数

因此直接左右找取最大值即可

求叶子结点数量

Code：

template<class T>
void BiTree<T>::CaculateLeafNum(BiNode<T> *root){
	if(!root) return;
	if(root->lchild == NULL && root->rchild == NULL) Leaf_Count++;
	CaculateLeafNum(root->lchild);
	CaculateLeafNum(root->rchild);
}

首先我们要知道叶子结点的特征：

没有儿子节点

（就是所有儿子节点都为 NULL）

所以左右搜找到无儿子 +1 即可

交换左右子树

template<class T>
void BiTree<T>::swap(BiNode<T> *root){
	BiNode<T> *temp;
	if(root == NULL)
		return;
	else{
		temp = root->lchild;
		root->lchild = root->rchild;
		root->rchild = temp;
		swap(root->lchild);
		swap(root->rchild);
	}
}

由于二叉链的本质就是指针的堆叠

因此直接交换指针的存值就可以了

Code

#include<bits/stdc++.h>
using namespace std;

template<class T>
struct BiNode{
	T data;
	BiNode<T> *lchild,*rchild;
};

template <class T>
class BiTree{
public:
	//构造 & 折构
	BiTree(){root = Creat(root);}
	~BiTree(){Release(root);}
	//遍历
	void PreOrder(){PreOrder(root);}
	void InOrder(){InOrder(root);}
	void PostOrder(){PostOrder(root);}
	void LeverOrder();
	//树的深度
	int  Depth(){Depth(root);}
	//叶子结点数量
	void CaculateLeafNum(){CaculateLeafNum(root);}
	//交换左右子树
	void swap(){swap(root);}
private:
	BiNode<T> *root;
	BiNode<T> *Creat(BiNode<T> *bt);
	void Release(BiNode<T> *bt);
	void PreOrder(BiNode<T> *bt);
	void InOrder(BiNode<T> *bt);
	void PostOrder(BiNode<T> *bt);
	int  Depth(BiNode<T> *root);
	void CaculateLeafNum(BiNode<T>* root);
	void swap(BiNode<T> *root);
};
int Leaf_Count = 0;

template <class T>
BiNode<T> *BiTree<T>::Creat(BiNode<T> *bt)
{
	T t;
	cin >> t;
	if(t == '#')
		bt = NULL;
	else {
		bt = new BiNode<T>;
		bt->data = t;
		bt->lchild = Creat(bt->lchild);
		bt->rchild = Creat(bt->rchild);
	}
    return bt;
}
template<class T>
void BiTree<T>::Release(BiNode<T> *bt){
	if(bt != NULL){
		Release(bt->lchild);
		Release(bt->rchild);
		delete bt;
	}
}

template <class T>
void BiTree<T>::PreOrder(BiNode<T> *bt){
	if(bt == NULL)
		return;
	else {
		cout << bt->data;
		PreOrder(bt->lchild);
		PreOrder(bt->rchild);
	}
}

template<class T>
void BiTree<T>::InOrder(BiNode<T> *bt){
	if(bt == NULL)
		return;
	else{
		InOrder(bt->lchild);
		cout << bt->data;
		InOrder(bt->rchild);
	}
}

template<class T>
void BiTree<T>::PostOrder(BiNode<T> *bt){
	if(bt == NULL)
		return;
	else{
		PostOrder(bt->lchild);
		PostOrder(bt->rchild);
		cout << bt->data;
	}
}

template<class T>
void BiTree<T>::LeverOrder(){
	int front = -1,rear = -1;
	BiNode<T> *Q[100];

	if(root == NULL) return;
	Q[++rear] = root;
	while(front != rear){
		BiNode<T> *q = Q[++front];
		cout << q->data;
		if(q->lchild != NULL) Q[++rear] = q->lchild;
		if(q->rchild != NULL) Q[++rear] = q->rchild;
	}
}

template<class T>
int BiTree<T>::Depth(BiNode<T> *root){
	int hl,hr;
	if(root == NULL)
		return 0;
	else{
		hl = Depth(root->lchild);
		hr = Depth(root->rchild);
		return max(hl,hr) + 1;
	}
}

template<class T>
void BiTree<T>::CaculateLeafNum(BiNode<T> *root){
	if(!root) return;
	if(root->lchild == NULL && root->rchild == NULL) Leaf_Count++;
	CaculateLeafNum(root->lchild);
	CaculateLeafNum(root->rchild);
}

template<class T>
void BiTree<T>::swap(BiNode<T> *root){
	BiNode<T> *temp;
	if(root == NULL)
		return;
	else{
		temp = root->lchild;
		root->lchild = root->rchild;
		root->rchild = temp;
		swap(root->lchild);
		swap(root->rchild);
	}
}

int main(){
	BiTree<char>* bitree=new BiTree<char>;
	cout<<"前序遍历";
	bitree->PreOrder();
	cout << endl;
	cout<<"中序遍历";
	bitree->InOrder();
	cout << endl;
	cout<<"后序遍历";
	bitree->PostOrder();
	cout << endl;
	cout<<"层序遍历";
	bitree->LeverOrder();
	cout << endl;
	cout<<"深度："<<bitree->Depth()<<endl;
	bitree->CaculateLeafNum();
	cout<<"叶子结点个数："<<Leaf_Count<<endl;
	bitree->swap();
	cout<<"左右子树交换后的层序：";
	bitree->LeverOrder();
	return 0;
}